

使用改进粒子群优化算法的FIR数字滤波器设计
描述
引 言
由于FIR数字滤波器具有系统稳定,容易实现线性相位,允许设计多通带(或多阻带)以及硬件容易实现等特点,使得其在数字信号处理中有着广泛的应用。传统FIR滤波器的设计方法是建立在对理想滤波器频率特性作某种近似的基础上进行设计的,其中包括窗函数法、频率采样法及最佳一致逼近法。窗函数法计算简单,但不能很好地折衷过渡带与幅频响应误差之间的矛盾。频率采样法直接从频域处理,原理简单,计算也不复杂,但不易精确确定其通带和阻带的边缘频率,并且使用传统的查表法,不能保证数据最优。最佳一致逼近法着眼于整个区间内的总误差为最小,但并不一定能保证在每个局部误差都最小。近年来许多学者将先进方法用于FIR滤波器优化设计,如神经网络法和遗传算法等。这些算法具备一定的有效性,但存在理论复杂,收敛速度慢,容易早熟收敛等不足。在此,提出一种改进粒子群优化算法(IMPSO)的FIR滤波器设计方法。该方法计算量小,整定时间短,并能有效克服早熟收敛的问题。
1 引入粒子聚合度的改进粒子群优化算法
1.1 粒子群优化算法(PSO)
PSO算法是美国Kennedy和Eberhart受鸟群觅食行为的启发,于1995年提出的。该算法的思想是通过种群粒子间的合作与竞争,产生群体智能指导优化搜索。PSO算法可用式(1)表示。
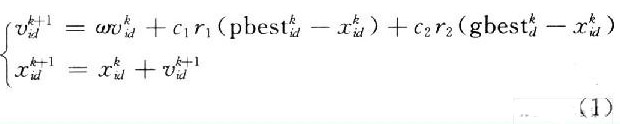
式中:vidk是粒子i在第k次迭代中第d维速度;xidk是粒子i在第k次迭代中第d维的位置;ω是惯性权值系数;pbestidk,是粒子i在第k次迭代中第d维个体极值点的位置(即个体最优);gbestdk是整个种群在第k次迭代中第d维全局极值点的位置(即全局最优);r1,r2是[0,1]之间的随机数;c1,c2是加速系数,或称学习因子。
1.2 带粒子聚合度的改进粒子群优化算法
由式(1)可知,如果粒子的当前位置在gbest,此时个体极值点与全局极值点为同一点,即pbest与gbest相同。这时粒子速度若等于零,则种群的粒子将会出现进化停滞,算法只能收敛到种群目前寻找到的最优解gbest。假如这时gbest对应的只是一个局部最优解,那么算法就出现了早熟收敛现象。
针对PSO算法存在早熟和局部收敛的问题,在基本PSO的基础上,加入粒子聚合度n和一个线性递减的惯性权值系数ω,对PSO算法进行改进。
聚合度n是用来反映粒子群*程度的一个系数。当粒子群出现高度*,进化停滞时,n随迭代次数递增;当n大于一个阈值λ(此阈值根据具体情况选择)时,对粒子进行变异,使变异粒子跳离当前位置,进入其他区域。在其后的搜索中,算法有新的个体极值pbest和全局极值gbest,从而跳出局部收敛。多次循环迭代后,就能找到全局最优。
改进的算法可用式(2)和式(3)表示:

式(2)中rand是[0,1]间的随机数:
式中:max Xd和min Xd分别是粒子在d维空间上的最大值和最小值。
惯性权值系数叫决定控制算法的收敛特性,当ω较大时,全局搜索能力强;当ω较小时,局部搜索能力强。文献[6]通过大量实验证明,如果ω随算法迭代的进行而线性减小,将显著改善算法的收敛性能。在此,取:

如果设计FIR数字滤波器的理想频率响应为Hd(ejω),则设计滤波器与理想FIR滤波器的误差e可通过对两滤波器的幅度在一定量的离散点上的误差平方和来表示,即取M个离散点时:
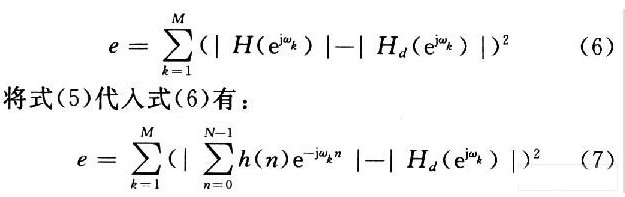
由式(7)容易知得,误差e是滤波器N个系数h(n)(n=0,1,…,N-1)的函数。对FIR滤波器的设计,就要选取合适的滤波器系数h(n),使误差e最小。显然,h(n)的选取是一个组合优化问题,因此可通过优化算法求解滤波器系数h(n),实现FIR设计。
2.2 适应度函数
IMPSO通过适应度函数来确定粒子当前位置的优劣,因此选式(7)作为优化设计FIR数字滤波器的适应度函数。即:
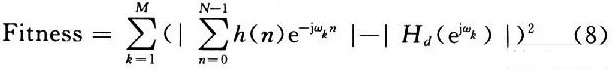
显然,Fithess函数值越小,则对应滤波器的幅度均方误差就越小,该粒子就对应更佳的滤波器系数。算法结束后,适应度最小的粒子所代表的参数值就是滤波器的最优系数。
2.3 算法编码及流程
为了用IMPSO算法求解h(n),应对优化参数h(0),h(1),…,h(N-1)进行适当的编码,以形成IMPSO算法中的粒子。算法用实数来表示各参数,h(0),h(1),…,h(N-1)分别表示N个粒子当前的位置;vh(0),vh(1),…,vh(N-1)分别表示当前粒子的速度;pbest(0),pbest(1),…,pbest(N-1)表示各粒子的个体最优,gbest表示全体的最优解。算法流程如图1所示。
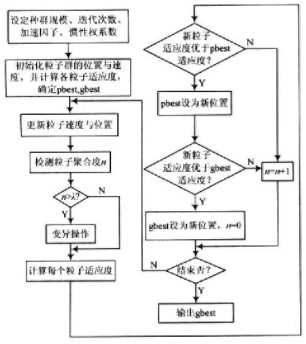
3 仿真算例
为了验证所提出算法的有效性,在计算机上采用Matlab语言进行FIR数字滤波器设计的仿真实验。同时为了比较算法性能,还采用基本遗传算法(BGA)和基本粒子群优化算法(BPSO)进行了相同的滤波器优化设计。仿真实验中,粒子群优化算法的参数设置为:群体大小Size=30,参数维数Codel=30,最大惯性权重为0.9,最小为0.2,聚合度为20,最大迭代次数为200;遗传算法参数设置为:种群30,遗传代数200,交叉概率0.5,变异概率0.1。

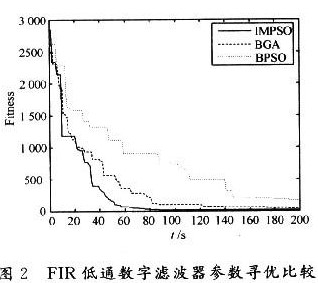
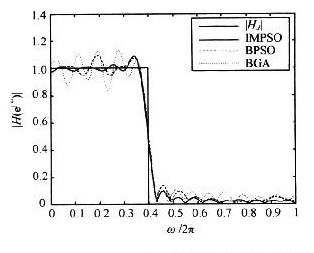
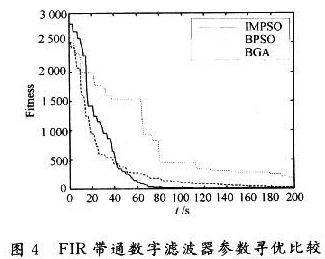
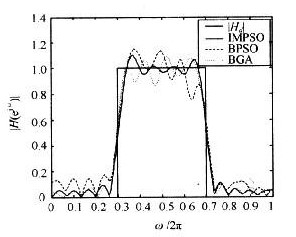
图3和图5则是用三种不同算法设计的FIR低通和带通数字滤波器。从图2和图4中容易看出,无论是对低通还是带通滤波器的设计,因为IMPSO对BPSO加入了聚合度检测,能进行智能变异,同时采用线性递减的惯性权值系数。因此与BPSO相比,IMPSO既有最快的寻优速度,也具有最好的适应值,只要迭代次数设置合理,在迭代次数范围内,粒子总会找到全局最优值。BPSO与BGA的寻优速度慢,容易陷入早熟收敛,很难得到理想的最优参数。由图3和图5的FIR低通与带通数字滤波器的幅频特性曲线可明显看出,利用IMPSO设计的滤波器在三种算法中最接近理想的滤波器,是较好的FIR滤波器设计方法。
4 结 语
在此通过加入聚合度,并将遗传算法中的变异思想引入到PSO算法中,对粒子实现智能变异,能有效克服标准.PSO容易进入局部收敛的缺点。同时由于该算法用到的参数少,程序实现简单,因此与BGA等其他算法相比,具有运算量少,寻优速度快等优点。通过实例仿真结果表明,这里提出的IMPSO算法在FIR低通与带通数字滤波器的设计上比BPSO和BGA具有更好的收敛速度和搜索能力。在设计FIR带阻和多通带数字滤波器时,IMPSO也是一种有效的设计方法。
-
数字滤波器是什么 数字滤波器的性能指标2023-02-24 6576
-
FIR数字滤波器设计2022-04-05 6490
-
基于FPGA的FIR数字滤波器该怎么设计?2019-09-29 2510
-
FIR数字滤波器优化设计2018-03-07 946
-
用CPLD实现FIR数字滤波器2017-01-10 932
-
基于Matlab/Simulink的FIR数字滤波器的设计与实现2016-01-15 1134
-
使用FPGA构建的数字滤波器设计方案2014-07-24 9464
-
基于FPGA的FIR数字滤波器的优化设计2011-08-16 4198
-
基于频率采样法FIR数字滤波器的设计2010-03-31 1219
-
基于LabVIEW的FIR数字滤波器设计2009-10-16 6667
-
基于DSP的FIR 数字滤波器设计2008-05-14 21453
-
什么是fir数字滤波器 什么叫FIR滤波器2008-01-16 17557
全部0条评论

快来发表一下你的评论吧 !

