通过Matlab软件实现对DSP/FPGA线性调频信号仿真

　　直接数字频率合成（DDS）是近年来得到迅速发展的一种新的频率合成方法，具有频率切换速度快，很容易提高频率分辨率、对硬件要求低等优点。可编程全数字化便于单片集成、有利于降低成本。提高可靠性并便于生产等有点。DDS技术从相位的概念出发进行频率合成，存储了数字采样波形表，可以产生点频、线性调频、ASK、FSK等各种形式的信号。线性调频信号可以获得较大的压缩比，有着良好的距离分辨率和径向速度分辨率，作为一种常用的脉冲压缩信号，已经广泛应用于高分辨率雷达领域。

　　Matlab是美国MathWorks公司自20世纪80年代中期推出的数学软件，优秀的数值计算与卓越的数据可视化能力使其很快在同类软件中脱颖而出。Matlab已经发展成为多学科、多种工作平台的功能强大的大型软件。本文用Matlab软件建立DDS系统中线性调频信号的仿真模型，对于理解线性调频信号和在FPGA中来实现线性调频信号有借鉴意义。

　　DDS线性调频信号发生器框图设计

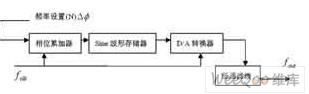
　　图 1 DDS技术的基本原理

　　1 DDS技术的基本原理

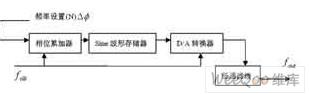
　　基本模型如图1所示，主要由时钟频率源fclk、相位累加器、波形存储器(ROM)、数/模转换器(D/A)、以及低通滤波器(LPF)组成。输出信号波形的频率表达式为：

　　

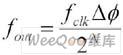
　　(1)式中，fclk为参考时钟频率，ΔΦ为相位增量，N为相位累加器的位数。只要N足够大，DDS可以得到很小的频率间隔。要改变DDS的输出信号的频率，只要改变ΔΦ即可。当参考时钟频率给定后，输出信号的频率取决于频率的控制字，频率分辨率取决于累加器的位数，相位分辨率取决于ROM的地址位数，幅度量化取决于ROM的数据字长和D/A转换器的位数。

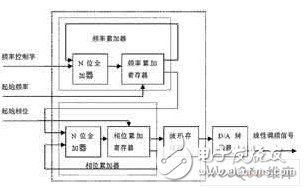
　　2 线性调频信号的实现框图

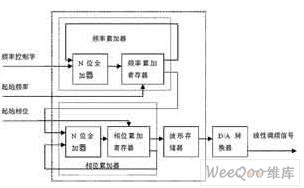
　　图2 软件编程实现线性调频信号的原理图

　　脉冲压缩雷达最常见的调制信号是线性调频信号，接收时采用匹配滤波器（Matched Filter）压缩脉冲。它的数学表达式如下：

　　

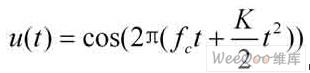
　　式中fe为载波频率，K=B/T是调频斜率，于是，信号的瞬时频率为。

　　其对应的量化公式如下（此式是以图2实现的原理公式）：

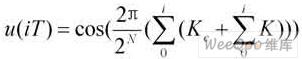　　(3)

　　式中N为相位累加器的位数，Kc为频率控制字，K为上式中的调频斜率。

　　图1所示的DDS原理框图是用于实现固定频率的正弦波信号，按照公式(3)的思路实时改变ΔΦ，即可产生线性调频信号。

　　经过频率累加器输出的是严格线性增长的瞬时频率。在实际过程中，相位累加器的输出是经过相位截断再进行寻址，从而引入了一定的相位误差，虽然这一误差会影响到线性调频信号的线性度，但是调频斜率为相位的二次导数，相位截断误差本身已很小，所以对调频线性度的影响就更小了。在本文的Matlab实现中暂时不考虑截断问题，忽略不计。

　　3 Matlab软件建模实现线性调频信号

　　本程序遵照上述软件编程实现线性调频信号的原理图编写，采用.m文件的方式编写，下面是实现的源程序：

　　%调频信号的累加器实现

　　clear all；clc   %清除所有变量，清屏

　　M=2^11； %采样的点数

　　a(1:1:M)=0； %频率累加器的数值

　　b(1:1:M)=0； %相位累加器的数值

　　y(1:1:M)=0； %输出的波形数据

　　K=400； %调频斜率

　　Kc=10；  %初始频率控制字

　　N=10；  %幅度量化位数

　　L=24；  %相位累加器位数

　　%下面一段实现频率累加器

　　a(1)=0.5*K； %初始频率步进量

　　for i=2:1:M

　　a(i)=a(i-1)+K；

　　end

　　%下面一段实现相位累加器

　　b(1)=Kc+a(1)； %相位初始值

　　for i=2:1:M

　　b(i)=b(i-1)+(Kc+a(i))；

　　end

　　%下面一段实现了查找表ROM以及进行幅度量化

　　for i=1:1:M

　　y(i)=floor(2^N*cos(2*pi/(2^L)*b(i)))；

　　end

　　%下面一段画出相应的图形

　　figure(1)；plot(y)；axis([0 M,-2^N-100 2^N+100])；

　　figure(2)；freqz(y)

　　上面这段程序中，有很多的变量，包括调频斜率K、频率控制字Kc、幅度量化位数N以及相位累加器位数L等等，修改不同变量值可以得到各，不同的线性调频信号。具体的实现要根据实际的需要来设置。

　　4 实验结果

　　根据上面的程序,取调频斜率为400，频率控制字为10，幅度量化为10位（和所使用的D/A配合），相位累加器为24位，用Matlab仿真得到的线性调频信号的波形和相应的幅频响应如图3和图4所示。

　　结束语图3 K=400，Kc=10，N=10，L=24的情况下的线性调频信号

　　图4 针对图3的幅频特性曲线

　　本文所讲的线性调频信号的产生原理和方法有很好的可扩展性，修改频率累加器的内容即可以实现其他的各种调频信号。作为线性调频信号，由于广泛应用于高分辨率的雷达系统中，因此正确理解线性调频信号的产生原理和掌握其产生的方法是很有现实意义的。在实际应用中主要采用专用DDS芯片或者FPGA来实现线性调频信号(各有优缺点)，而本文则基于Matlab软件的良好编程性来验证这一方案，仿真结果较好的证明本方案的可行性，完成了预期的方案设计和论证。