

改进型64倍降采样数字抽取滤波器的设计与仿真分析
描述
1 引言
∑-△调制器与数字抽取滤波器是∑-△ ADC 实现16bit 以上精度的关键电路模块。∑-△调制器依靠过采样与高阶闭环负反馈控制实现的噪声整形技术,将基带内的量化噪声搬移到高频段,而数字抽取滤波器则将带外高频段的噪声加以滤除,同时将输出频率降低到输入信号的奈奎斯特采样频率,最终实现对输入信号高精度的模数转换。
由于采用过采样技术,∑-△ ADC 对输入信号带宽有一定限制,比较适合低频信号的模数转换。
以音频信号44kHz 的奈奎斯特采样频率为例,在64倍的过采样率下,即输入采样频率为2.816MHz,4阶∑-△调制器可实现16bit 的转换精度;输出PDM信号经* 倍降采样数字抽取滤波器的处理后恢复初始信号的奈奎斯特采样频率。为保持S - Δ调制器的精度性能,数字抽取滤波器的通带截止频率应为20kHz、阻带起始频率为24kHz、阻带衰减最小为80dB、通带纹波为± 0.01dB、ADC 有效位数大于15bit。
∑-△ ADC 的精度和转换速度由∑-△调制器决定,其中∑-△调制器的阶数、过采样率等参数直接决定了ADC 的分辨率,一般只需小规模的数模混合电路即可实现,面积小且功耗低。用于滤除量化噪声的数字滤波器,为维持调制器的高分辨率就必须具有一定量的阻带衰减与很小的纹波,导致数字滤波器的阶数过大,并直接导致硬件消耗与功耗的显着增加。
本文针对高精度数字抽取滤波器IP 电路,进行低成本与低功耗设计技术研究。在给定指标约束下,通过对CIC 抽取滤波器结构的改进,同时将多相结构应用到补偿滤波器和半带滤波器中,获得比经典结构在硬件消耗与功耗上明显的降低。
2 经典 CIC 滤波器结构
为确保数字滤波器信号的出路精度,采用单级抽取滤波器的阶数将与输入信号的采样频率成正比,而与过渡带宽成反比。对于输入频率2.816MHz、过渡带宽4kHz 的设计指标,采用单级抽取结构的滤波器,由于频率高、过渡带窄而导致单级滤波器阶数过大,可实现性差,因此采用多级抽取结构成为必然。在多级结构中,第一级抽取结构的输入频率为系统最高的输入频率,但它的过渡带宽很大;最后一级虽然过渡带宽很窄,但输入频率降低;中间级的输入频率与过渡带宽均较为适中,这样的频率与过渡带分布配置,使得最终各级滤波器的总阶数远小于单级抽取的阶数,因此多级结构更具有实用价值。
CIC 是由Hogenauer提出的一种无需使用乘法器的滤波器结构,结构简单,采样变换率高,可作为多级数字抽取滤波器中的输入级。阻带衰减为衡量CIC 性能的一个重要指标,在Matlab 下对抽取因子为64、32、…、2 的最小阻带衰减进行仿真,确定当抽取因子最大为16 时,阻带衰减仍满足设计要求,继续增大抽取率导致性能下降,则最大抽取倍率为16。
CI C 滤波器的最大缺陷在于通带内的过多衰减,后面必须加一级补偿滤波器以确保补偿后的通带纹波仍满足指标要求,补偿滤波器同时还具备降采样抽取功率,可选择4 倍抽取,也可先进行2 倍抽取,然后用一级半带滤波器再完成2 倍抽取。基于多级抽取有利于降低硬件资源与功耗的原则,64倍降采样数字抽取滤波器可采用如图1 所示的三级结构。
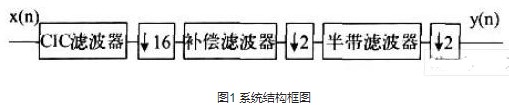
图1 系统结构框图
CIC 降采样滤波器对系统性能的影响至关重要,其级联级数D与S-Δ调制器的阶数L之间存在D=L+1的关联,对于4 阶∑-△调制器,D=5,在16 倍降采样率下,CIC 滤波器的系统函数为:
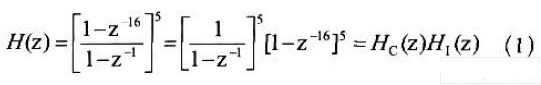
采用Hogenauer 经典结构实现以上系统传输特性时,可将级联梳状滤波器分解为积分器HC(z)与梳状微分器HI(z)两部分,然后采用层叠结构实现。
由于HI(z)中的延迟因子需要16 个寄存器,采用置换原则,完成16 倍抽取后再进行微分部分的计算,这样就只需要一个延迟因子,由此得到如图2 所示的经典CIC 电路结构框图。

图2 经典CIC滤波器电路结构
CIC 中由于没有乘法运算,同时置换原则的应用大大减少了寄存器的数量,面积和功耗得到有效控制。但是,经典CIC 结构的很大缺陷在于其中的积分器HC(s)为IIR 滤波器,即存在的输出到输入反馈使系统稳定性无法保证,并导致数据溢出。设CIC 滤波器的级联级数为N,抽取倍数为M,输入与输出位数分别为Bin 和Bout,则两者间必须满足以下关系:
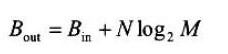
根据设计指标要求,Bin=1bit、M=24、N=5 时,Bout=21bit,即整个电路中所有寄存器和加法器位数为21 位时,系统才不会产生溢出,而输出位数的大小决定了寄存器的位数以及涉及的计算量,并由此影响功耗与面积。
最终决定数字滤波器面积的是寄存器单元数量,通过估算其中1 位寄存器的数量可比较芯片面积的相对大小;由于没有乘法器,则加法运算决定了CIC 滤波器中的功耗,以1 个1 位加法器在一个输出周期内完成的加法次数作为估算功耗的基本单位。
图2 中,一共有10 个延迟因子,若每个字长均取21 位,一共需要210 个1 位寄存器。总共有10 个21 位加法器,5 个工作在输入频率,5 个工作在输出频率,等效功率因子为:
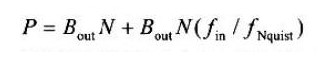
计算得到等效功率相对因子为6 825,较大的功耗表明针对功耗面积优化的CIC 尚有继续改进的空间。
3.CIC 滤波器的改进设计
经典CIC中IIR传递函数的递归结构严重制约了CIC 滤波器的性能,消除IIR 成为改进CIC 设计的基本出发点。将H(z)中的分子多项式因式分解并通过约分得到:
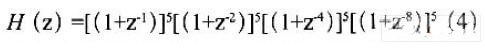
上式中没有IIR 结构,从而消除了输出到输入的递归运算,确保系统稳定,结合置换原则,由此得到改进的CIC 电路结构如图3 所示。

图3 非递归结构CIC滤波器的实现框图
这种非递归结构所需要的1 位寄存器总数为R=1+2+3+?+20=210,而等效功耗因子P=(2+3+4+5+6)×16+(7+8+9+10+11)×8+(12+13+14+15+16)×4+(17+18+19+20+21)×2=1 130。与经典结构相比,寄存器总数相等,但功耗减小到原来的1/ 6,采用这种非递归结构不但改善了系统稳定性,还大大提高了系统性能。由于电路实现时需采用层叠结构,5级结构即需5 级层叠,如果其中有一级为4 或者更小,那就可以减小层叠数,从而进一步减小硬件和功耗。
阻带衰减为衡量CIC 滤波器性能的一个重要指标。通过牺牲部分阻带衰减性能可减小层叠数。对于4 级结构,应分别考虑各级在需要的衰减频段处能达到的衰减值。在Matlab下分别仿真(1+z-8)、(1+z-4)、(1+z-2)、(1+z1)的幅频特性,并依次设为第一级到第四级。设CIC 滤波器的零点为FZ,根据设计指标,中心频率fC=22kHz,只要在所有FZ ± fC频率范围内阻带衰减值能达到80dB,CIC滤波器即可满足设计指标要求。由于最小衰减值出现在FZ-fC 与FZ+fC 关键频率点处,在Matlab 下仅测试单级时关键频率点处的阻带衰减,结果如表1 所示。
表1 各级为单级时在关键频率点处的阻带衰减值
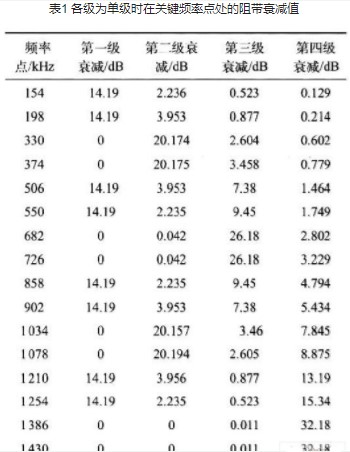
通过计算,当第一级到第四级的级联级数分别减小为最低的5、4、3、3 时,则最小阻带衰减量计算为:
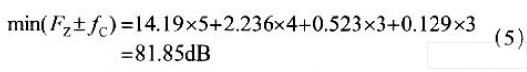
虽然以上降低层叠数的改进结构其最小阻带衰减满足设计要求,但后级补偿滤波器无法使纹波达到设计要求,应加大其中一级或两级的级联级数来降低补偿后的通带纹波,将级数增大后纹波的变化如表2 所示。
表2 级数增大后补偿结果的变化
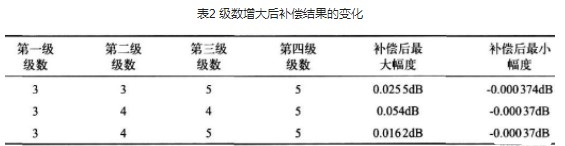
只有当级联级数为3、4 、5 、5 时补偿后的结果接近设计指标要求。将补偿后的整体幅频特性沿着Y 轴方向向下移动约0.008dB 左右,这样最大纹波为0.016 2-0.008=0.008 2dB,最小纹波为-0.000 37-0.008=-0.008 37dB,这样纹波就在指标范围内,所以采用这种级联方式可以满足设计指标要求。最终确定的CIC 滤波器系统函数为:
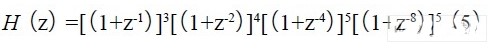
图4 为改进前后CIC 滤波器的幅频响应,实线与虚线分别对应为改进前后的幅频响应,改进后的曲线比改进前有明星的上升,部分点处上升的幅度还较大。但由于改进后在关键点处能够达到衰减的性能要求,牺牲其他非关键点处的衰减特性以降低硬件资源和功耗的设计策略还是非常可取的。
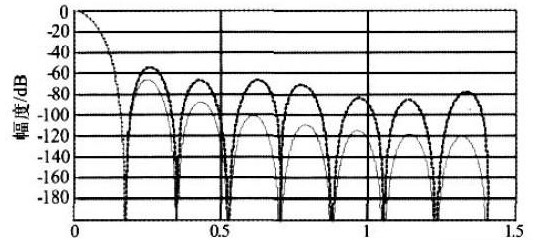
图4 改进前后的幅频响应比较
此时,寄存器总数降低到R=1+2+3+?17=153,等效功耗因子P 降低为P=(2+3+4)× 16+(5+6+7+8)×8+(9+10+11+12+13)×4+(14+15+16+17+18)×2=732,比未改进前少用了57 个寄存器,功耗则降低了35%,在保持纹波性能的前提下,硬件资源消耗和功耗明显降低。
4 补偿滤波器与半带滤波器设计
改进后的CIC 滤波器幅频特性整体向上偏移,导致通带频率处的各点频率向上移动,与改进前幅度相同的点在改进后的曲线上必然向前移动,即改进后的频率点相当于左移。所以,针对改进后的CIC 滤波器设计补偿滤波器时,其通带截止频率点相应地也要左移。若将通带截止频率设为小于20kHz 的点,通过调整参数以优化补偿后的纹波性能,即调整幅频特性曲线后最终得到的通带纹波为±0.006 2dB。
补偿前后的通带特性如图5 所示,图中下方曲线为CIC 滤波器在通带范围内的幅频响应,上方曲线为补偿滤波器的幅频响应,中间部分为补偿后的幅频响应。显然,经补偿后的曲线在通带范围内变得更加平坦。
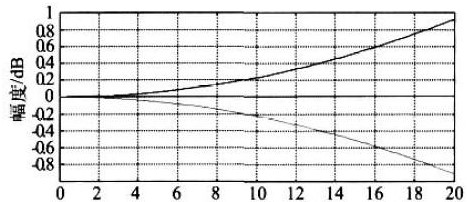
图5 补偿前后的通带幅频特性
补偿滤波器系统传递函数可采用如图6所示的多相结构实现方式。若采用传统的直接型结构实现,所有的运算单元将工作在2倍抽取频率之前,功耗较大。
而多相结构中,由于补偿滤波器中所有的加法与乘法单元都工作在输出频率而非输入频率处,这样在面积没有增加的情况下,功耗将比直接型结构节省近50%。
半带滤波器完成最后的2 倍降采样抽取,并使数字滤波器的总体性能达到指标要求。在Matlab 下调用相应的函数设计半带滤波器,其通带和阻带幅频特性如图7 和图8 所示。
同样采用多相结构实现半带滤波器,得到的电路结构如图9 所示。如果采用直接型结构,则需要的寄存器数为102,而多相结构的应用可使寄存器数降低到76 个,面积有一定程度的下降,并且由于所有运算单元直接工作在输出频率,功耗也比直接型结构降低了50%。
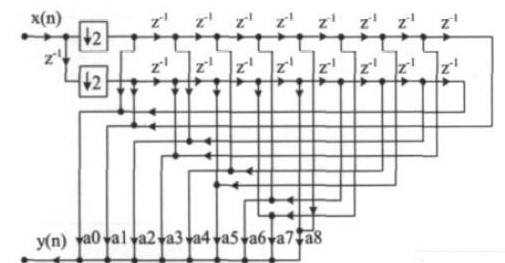
图6 补偿滤波器的多相实现结构
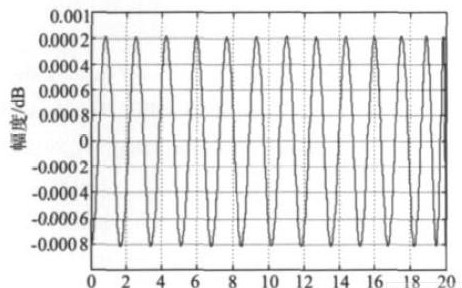
图7 半带滤波器的通带幅频响应
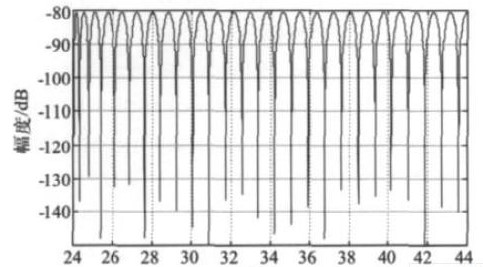
图8 半带滤波器的阻带幅频响应
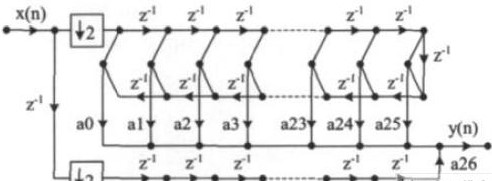
图9 半带滤波器的多相结构
5 仿真与验证
在matlab 下对64 倍降采样及连抽取滤波器的幅频响应进行仿真,结果如图10 所示,其中补偿滤波器和半带滤波器的系数经过了截位处理。
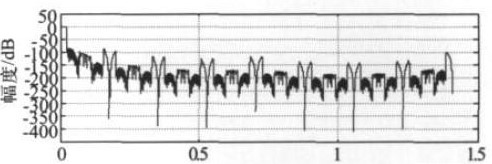
图10 系统总幅频特性曲线
对数字滤波器的通带纹波与阻带衰减特性进行仿真,相应的幅频响应曲线如图11和图12所示。系统总通带纹波为± 0.006dB,阻带衰减在80dB以下,总体性能满足设计要求。
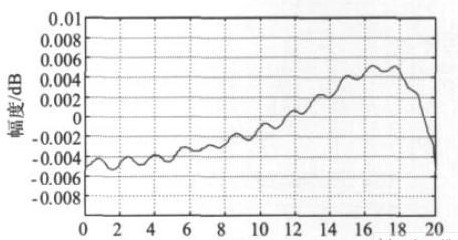
图11 系统通带特性
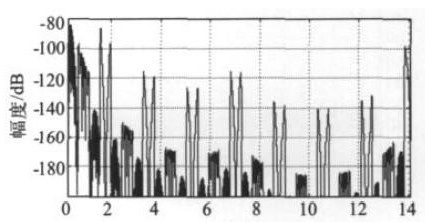
图12 系统阻带特性
在Mat l ab 下建立整个抽取滤波器的模型,用Matlab工具包生成 ∑-Δ调制器的输出信号进行系统测试,输出结果如图13 和图14 所示。
由于量化噪声被基本滤除,滤波器的输出得到所需的正弦信号。对整个抽取滤波器完成VerilogHDL 描述,其中运用了Horner 法则以提高精度,采用CSD 码对乘系数进行编码,乘法器直接采用移位和加法实现。最后,选用EP2C8Q208C8 并基于Quartus 工具综合了整个抽取滤波器,系统共占用FPGA 的LE资源达5 435 个,约占总数的66%。综合后可得到的最高时钟频率为5 5 . 9 5MHz ,并且对Modelsim 下后仿输出的数据进行了FFT 分析,并计算其相应的信噪比,图15 为5kHz 信号的FFT输出结果。

图13 调制器输出信号
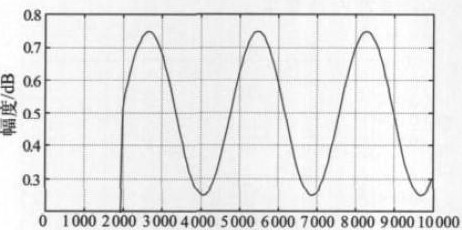
图14 滤波器输出信号
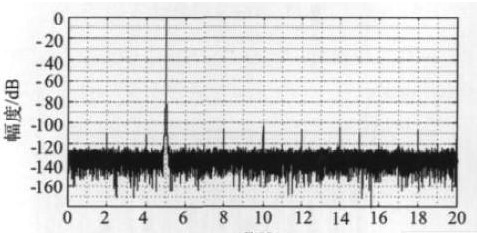
图15 5kHz 信号FFT 分析结果图
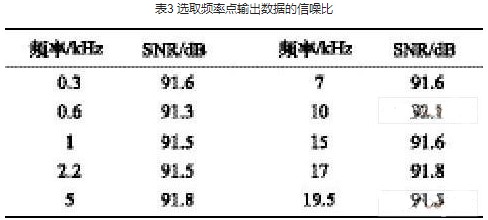
在0~20kHz 范围内选择足够的频率点进行测试,测试结果如表3 所示,输出数据的有效位数均满足大于15bit 的设计要求。
表3 选取频率点输出数据的信噪比
6 结论
本文提出了一种面积小功耗低的数字抽取滤波器的设计。设计结构在过采样率很高时更能体现出它的优势。通过适当牺牲CIC 滤波器的阻带衰减特性以换取精度与硬件资源之间的平衡折衷,面积略有下降而功耗则比经典结构降低了35%;采用多相结构实现补偿滤波器和半带滤波器,均可使其功耗降低近50%,同时半带滤波器的硬件消耗也有明显下降。通过FPGA 验证,改进后的64 倍降采样抽取数字滤波器可满足15bi t 精度处理的要求。
-
 luowhu
2019-05-22
0 回复 举报然道只有我看出来他相对功耗算错了吗 收起回复
luowhu
2019-05-22
0 回复 举报然道只有我看出来他相对功耗算错了吗 收起回复
-
CIC抽取滤波器MATLAB仿真和FPGA实现2021-08-17 2945
-
怎么样使用FPGA设计ADC数字抽取滤波器2020-08-26 1362
-
FPGA的FIR抽取滤波器设计详细教程2018-04-19 2746
-
高频数字抽取滤波器的设计2018-02-21 2294
-
数字下变频中抽取滤波器的设计及FPGA实现2017-11-17 6480
-
改进型倍流整流电路ZVS PWM全桥变换器的研究2017-09-12 1159
-
一种改进型比例积分环路滤波器的设计2017-01-07 908
-
4阶24倍抽取CIC滤波器设计2016-04-27 1381
-
零基础学FPGA(三十一)写在京城,Hogenauer CIC抽取滤波器的FPGA实现笔记2015-08-29 19542
-
∑-△ADC的降采样滤波器方案2012-03-19 6471
-
数字滤波器设计2012-02-26 6996
-
级联COSINE滤波器在抽取滤波中的研究2011-05-03 862
-
CIC抽取滤波器的改进及其FPGA的实现2011-03-15 881
-
一种性能良好的高效CIC抽取滤波器的设计2010-06-02 2056
全部0条评论

快来发表一下你的评论吧 !

