自适应均衡器的LMS和RLS两种算法的特性与仿真分析

自适应均衡属于自适应信号处理的应用范畴，各种各样的自适应均衡算法如迫零（ZF）算法、最小均方（LMS）算法、递归最小二乘（RLS）算法、变换域均衡算法、Bussgang 算法、高阶或循环统计量算法、基于非线性滤波器或神经网络的均衡算法等应运而生。均衡器通常工作在接收机的基带或中频信号部分，基带信号的复包络含有信道带宽信号的全部信息，所以，均衡器通常在基带信号完成估计信道冲激响应和解调输出信号中实现自适应算法等，本文选择了两种典型的自适应算法：以LMS自适应均衡器和RLS自适应均衡器为基础，用MATLAB 仿真软件对LMS和RLS两种算法进行仿真，比较并分析了两种算法的性能。

1 自适应均衡器

一种均衡器，可用于校正高速双极性信号的符号间干扰。它可响应电话线路的静态和动态性能变化。均衡器包括若干级逻辑控制线路及抽头线路，每个抽头线路有一个积分器，积分器由电子开关控制进行充电放电。积分器的输出在逻辑控制下相加或相减。均衡信号还可以在线路变压器处直接监视。

自适应均衡器的工作过程包含两个阶段，典型的训练序列是伪随机二进制信号或一个固定的波形信号序列，紧跟在训练序列后面的是用户消息码元序列。接收机的自适应均衡器采用递归算法估计信道特性，调整滤波器参数，补偿信道特性失真，训练序列的选择应满足接收机均衡器在最恶劣的信道估计条件下也能实现滤波器参数调整。所以，均衡器参数基本上接近最佳值，以保证用户数据的接收，成为均衡器的收敛。用户数据序列需要被分割成数据分组或时隙分段传送。无线通信均衡器原理简图如图1所示。

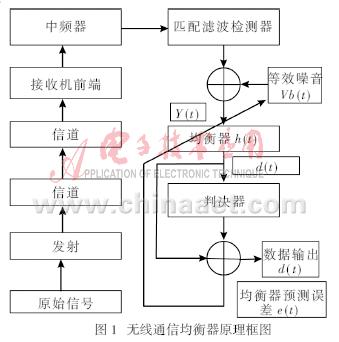
图1中，原始信号为x（t），h（t）是发射机、无线信道和接收机射频/中频级合在一起的系统等复合滤波器的冲激响应，所以均衡器的输入可表示为：

式中H（t）是H（t）的复共轭，高均衡器机射频/中频级合在一起的系统等复滤波器冲激响应。设均衡器的冲激响应是heq（t），均衡器输出码元波形可表示为：

2 自适应均衡算法

利用自适应均衡器补偿未知时变信道的特性，需要采用有效的算法跟踪信道特性变化来更新均衡器的加权系数。

2.1 基于LMS的自适应均衡算法

感知器和自适应线性元件在历史上几乎是同时提出的，并且两者在对权值的调整的算法非常相似。它们都是基于纠错学习规则的学习算法。感知器算法存在如下问题：不能推广到一般的前向网络中；函数不是线性可分时，得不出任何结果。而由美国斯坦福大学的Widrow和Hoff在研究自适应理论时提出的LMS算法，由于其容易实现而很快得到了广泛应用，成为自适应滤波的标准算法。

LMS算法[1]采用的是最小均方误差准则，代价函数是：

2.2 基于RLS的自适应均衡算法

RLS算法[3]所采用的准则是最小二乘准则，其代价函数为：

3 仿真结果分析

为了更直观地描述，考虑一个线性自适应均衡器。随机数据产生双极性的随机序列x[n]，它随机地取+1和-1。随机信号通过一个信道传输，信道性质可由一个三系数FIR滤波器刻画，滤波器系数分别是0.3、0.9、0.3。在信道输出加入方差为σ平方的高斯白噪声，设计一个有11个权系数的FIR结构的自适应均衡器，令均衡器的期望响应为x[n-7]，选择几个合理的白噪声方差σ平方。

采用基于LMS和RLS的自适应均衡算法分别进行实验，画出一次实验的误差平方的收敛曲线，给出最后设计滤波器系数。一次实验的训练序列长度为500。进行20次独立实验，画出误差平方的收敛曲线。采用基于LMS的自适应均衡算法，在相同信噪比，忘却因子分别为μ=1.5、μ=1和μ=0.4的情况下，20次实验误差平方的值曲线分别如图2、图3和图4所示。采用RLS法，在相同信噪比，忘却因子分别为μ=1、μ=0.8和μ=0.6的情况下，20次实验误差平方的均值曲线分别如图5、图6和图7所示。

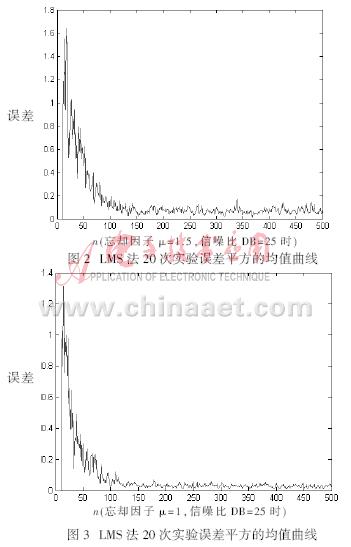
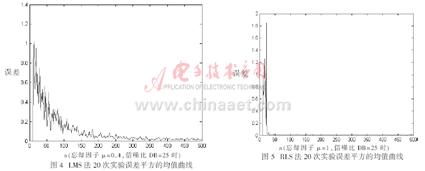
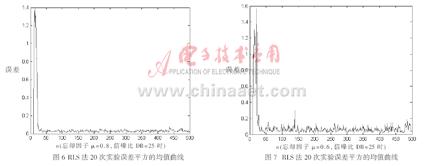
通过上述仿真结果可以看出，观察三个不同步长情况下的平均误差曲线，步长越小，平均误差越小，但收敛速度越慢，为了好的精度，必然牺牲收敛速度。RLS算法的收敛速度明显比LMS算法快，并且误差也比LMS算法小。当忘却因子趋于0时，RLS算法也就是LMS算法。

通过仿真可以看出相同忘却因子下，RLS算法的收敛速度明显比LMS算法快，并且误差也比LMS算法小。当忘却因子趋于0时，RLS算法也就是LMS算法。LMS和RLS都还有很多改进的算法，进一步的工作就是继续分析这些算法，并且不断完善系统模型。