

如何利用隐马尔可夫质量控制模型进行质量评估
描述
信息工程监理,就是监理服务商依照有关技术标准与规范、法律法规、业主需求以及业主与承建方签定的合同,本着科学、公正、严格、守信、遵纪、守法的原则,以高度的责任心、丰富的管理经验和专业技术能力,帮助业主审核建设承包合同条款、掌控工程进度和质量、进行成本核算,按期分段对工程进行验收,对工程建设项目实施全面而有重点的、精线条的监督管理,保证工程高质量地、按期完成,最终提交业主满意的成果。因此,信息工程监理的宗旨,就是协助业主进行项目管理,帮助业主防范工程建设中可能出现的各种风险,最终维护业主的合理利益。本文通过对信息工程质量监理过程特点的分析,将隐马尔可夫模型映射到质量监理中,利用前向算法估计出在该模型下观测事件序列发生的概率,从而在一定程度上有助于对软件质量进行定量控制。
1 模型的建立
1.1 特征提取
隐马尔可夫模型(Hidden Markov Model,HMM)作为一种统计分析模型,创立于20世纪70年代。80年代得到了传播和发展,成为信号处理的一个重要方向,现已成功地用于语音识别,行为识别,文字识别以及故障诊断等领域。隐马尔可夫模型是马尔可夫链的一种,它的状态不能直接观察到,但能通过观测向量序列观察到,每个观测向量都是通过某些概率密度分布表现为各种状态,每一个观测向量是由一个具有相应概率密度分布的状态序列产生。所以,隐马尔可夫模型是一个双重随机过程----具有一定状态数的隐马尔可夫链和显示随机函数集。自20世纪80年代以来,HMM被应用于语音识别,取得重大成功。到了90年代,HMM还被引入计算机文字识别和移动通信核心技术"多用户的检测".近年来,HMM在生物信息科学、故障诊断等领域也开始得到应用。
将隐马尔可夫模型映射到信息工程监理质量评估模型上,即一个软件的质量状态是无法直接观察到的,但是可以通过分析与这个软件相关的质量度量要素,估算该软件的质量状态,从而进一步得到其量化的评判值。信息化工程监理国标中的信息化工程监理规范技术参考模型,将信息工程质量监理分为工程招标、工程设计、工程实施和工程验收四个阶段。各个阶段的软件质量状态构成一个马尔可夫链,度量要素序列是一个随机过程,每一个度量要素会对软件的质量状态的转移带来一定影响,这样,度量要素序列和软件的质量状态之间就构成了一个隐马尔可夫模型。通过观察信息工程监理全过程各个阶段的度量要素,每个阶段都可以得到一个随机的度量要素序列,这样就可以计算软件的质量状态和评判值。
软件质量目标控制按照分层法分解为人、软件元、开发方法、设备及材料和工程环境五个度量要素,软件质量状态依据各度量要素分为优、良、中、差四个决断因子,如果再定义出它们之间的概率转换关系,就会得到由这两组状态构成的隐马尔可夫模型(如图1所示)。

根据该HMM模型,可以在没有直接观测软件质量的情况下根据度量要素的分布来推测软件质量的变化情况。

如果能较为准确地计算软件质量处于何种状态,则可以定量分析软件的质量情况。软件质量状态之间的转移见图2.

由图1可以直观看出,度量软件质量的要素有5个,用V={P,U,M,F,E}表示,ν1=P(People),表示度量要素人的因素;ν2=U(Units),表示度量要素软件元质量;ν3=M(Methods),表示度量要素开发方法;ν4=F(Facilities),表示度量要素设备及材料;ν5=E(Environment),表示度量要素工程环境。设质量度量要素观测序列为O={o1,o2,o3,o4},其中ot∈V.
设软件质量情况在信息工程监理开始阶段状态为π,它是一个向量,表示在信息工程监理工程招标阶段软件质量处于各个状态的概率,π={π1,π2,π3,π4},πi=P(q1=si),1≤i≤4.对于工程招标阶段,可以根据信息工程监理协同工作平台下的模糊因素神经网络质量评估方法得到一个默认值,之后的每一阶段,通过Trans和Obs可以计算出当前软件质量处于各种状态的概率st=(r1,…,r4),将此概率作为下一阶段的初始状态。在t阶段,状态分布表示为rt={rt(i)},1≤i≤4,状态的分布概率公式为:rt(i)=P(qt=si|λ)。再引入一个代价向量C[10],代表软件在每个状态的质量值,则可以将软件状态的定性分析转化为定量分析。
设Trans为软件质量状态转换矩阵,即质量状态之间转换的概率组成的矩阵,包含4行4列,aij表示在t阶段质量状态为si,那么到t+1阶段质量状态为sj的概率,即aij=P(qt+1=sj|qt=si),1≤i,j≤4.
定义Obs为当软件处于某一个特定质量状态时观测到某种度量要素的概率矩阵,bj(k)表示在阶段t,软件质量处于sj状态观测到度量要素νk的概率,1≤k≤5,1≤j≤4.
2 基于前向算法的模型应用
根据得到的观察序列O={o1,o2,o3,o4}和模型λ=(π,Trans,Obs)可以计算出在该模型下观察事件序列发生的概率P(O|λ)。P(O|λ)评价了给定模型?姿与给定观测序列匹配的程度。
对隐马尔可夫模型而言,状态转换序列是隐藏的,一个观测序列可能由任何一种状态转换序列产生。因此要计算一个观测序列的概率值,就必须考虑所有可能的状态转换序列。
穷举搜索的时间复杂度是2TNT,前向算法的时间复杂度是2N2T,其中T指的是观察序列长度,N指的是隐藏状态数目。对于信息工程监理质量控制,N=4,T=4,如果利用穷举搜索算法,复杂度相对会比较大,可以采用前向算法来降低复杂度。

给定这种算法,对于已知的一个度量要素观察序列,可以直接用来确定在一些隐马尔可夫模型中哪一个最好地描述了它,即先用前向算法评估某一个给定的λ,然后通过多次调整参数λ来提高评估的概率,进而通过实时调整信息工程监理中的质量的度量要素的比例来达到提高软件质量控制的目的。
3 仿真实验
实验数据于信息工程监理协同工作平台(IPSS)下的数据库。实验环境为Eclipse和Java开源工具包jahmm-0.6.1.文中使用状态数为N=4,观测值数为M=5的隐马尔可夫模型进行检验。
在信息工程监理中,每个阶段软件所处的质量状态与前一阶段所处的质量状态有关,即前一阶段的质量状态会影响下一阶段质量状态出现的概率。
初始质量状态概率分布:π=(0.3,0.3,0.2,0.2)
四个质量状态两两之间转化的概率如表1所示。

软件质量处于某个状态时,度量要素所占的比例有一定的规律性。度量要素观测值概率分布如表2。
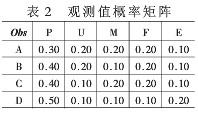
下面根据软件质量初始状态、表1和表2的数据,估计状态序列O={P,U,M,F}出现的概率。假设P为工程招标阶段观测到的主导要素,U为工程设计阶段观测到的主导要素,M为工程实施阶段观测到的主导要素,F为工程验收阶段观测到的主导要素。
在模型λ下,在t时刻观测事件是ot、状态是si的概率如表3所示,每个阶段的四个概率对应四个质量状态。


本文通过对隐马尔可夫理论的分析,建立了用于质量控制的隐马尔可夫模型,并尝试基于该模型对信息工程监理进行质量控制。本文提出的隐马尔可夫质量控制模型只是用于控制信息工程监理4个阶段的5个基本要素,模型稍显粗糙。如何基于隐马尔可夫模型或其他扩展模型与信息工程监理质量控制完全的整合,以及如何利用模型进行质量评估并对模型进行训练还需要进一步的探索研究。
-
基于隐马尔可夫模型的音频自动分类2011-03-06 1863
-
基于概率的统计分析隐马尔可夫模型2019-08-20 907
-
隐马尔可夫模型的组成2019-10-14 1692
-
基于隐马尔可夫模型的火焰检测2009-04-14 1033
-
基于隐马尔可夫的系统入侵检测方法2009-08-05 639
-
隐马尔可夫模型(HMM)攻略(有具体例子-方便理解)2016-12-07 1168
-
基于隐马尔可夫模型的视频异常检测模型2017-11-20 1212
-
基于改进的隐马尔可夫模型的态势评估方法2017-12-03 866
-
基于隐马尔可夫模型的短波认知频率选择方法2017-12-18 1051
-
基于隐马尔可夫模型的软件状态评估预测方法2018-01-05 967
-
基于隐马尔可夫预测的功率博弈机制2018-02-02 1090
-
基于耦合多隐马尔可夫模型人体动作识别2018-03-29 1122
-
改进隐马尔科夫模型的网络态势评估方法2021-05-31 911
-
基于隐马尔科夫模型的恶意域名检测方法2021-06-08 896
-
基于隐马尔科夫模型的公交乘客出行链识别2021-07-02 753
全部0条评论

快来发表一下你的评论吧 !

