差分跳频技术的原理、特点及在AWGN的多用户能力分析

1 差分跳频

相关差分跳频（DFH）通信是近年出现的跳频通信方式。美国Sanders公司研制的相关跳频增强扩谱CHESS电台就采用这种差分跳频技术，实现了在短波波段5 000跳/秒的跳频速率和最高19.2 kbit·s-1的数传速率。

差分眺频的基本原理：当前时刻的工作频率fn由上一跳的工作频率fn-1和当前时刻的信息符号Dn决定，即

fn=G（fn-1,Dn）

其中，G（fn-1,Dn）是一个特定函数，文中称为G函数，它决定了差分跳频的数据/频率映射关系。由此可见，相邻跳变频率之间通过数据序列建立了一定的相关性，亦即相邻频率的相关性携带了待发送的数据信息，因此这种跳频方式也被称为相关差分跳频。

2 差分跳频技术的特点

差分跳频技术集跳频图案、信息调制与解调等功能于一体，构成与传统跳频技术完全不同的技术体制，它具有以下特点：

（1）差分跳频体制是一种相关跳频体制，差分跳频通过G函数变换，使相邻或多跳频率之间具有相关性，其相关性携带了待发送的数据信息，收端也是根据其相关性还原数据信息，所以也将这种跳频体制称为相关跳频。在常规跳频体制中，时间上相邻的频率与其传输的数据信息无关。

（2）差分跳频体制是一种异步跳频体制，差分跳频的收端无法预知每个时刻的发端频率，在工作带宽内进行宽带数字化接收，接收端不需要频率合成器，从这个意义上说，差分跳频是一种异步跳频。

（3）G函数具备数据的调制解调功能，差分跳频无需传统定频或跳频体制中的基带和中频调制，发端经G函数变换，实现数据与频率之间的"数/频"编码，收端先对接收到的直接携带信息的射频频率进行有效检测，再经过G函数的逆变换即可恢复出数据信息，实际这也是一种调制解调过程。相同的情况，这是差分跳频图案产生的机理决定的，普通跳频一般不具备这个特点。

（4）跳频图案没有实时时间参与运算在传统跳频图案产生过程中，除跳频时序控制以外，原始跳频密钥Pk和时间参数TOD参与跳频图案运算。而在差分跳频图案的产生过程中，数据流参与跳频图案的运算，相当于跳频密钥，与实时时间TOD无关。数据流对跳频通信的接收端是未知的。

由于差分跳频与传统跳频的原理有很大差别，造成其组网性能也有很大不同。例如，传统跳频电台组网时，相同频率造成频率碰撞，形成多址干扰，而频率不同时，不构成多址干扰；对于差分跳频电台，不同频率可能会造成接收方数据的误判，从而形成多址十扰；频率相同时，如果削弱有效频率的幅度，则形成多址干扰，如果加强频率的幅度，则不形成多址干扰，与两个频率之间的相位有关。

传统的同步组网是指，各跳频网在技术体制、跳频图案算法及跳频密钥相同以及同一张频率表的条件下，各跳频网每一跳的起跳时刻相同，并且任一时刻的各网瞬时频率正交。由于传统的同步组网是同频造成多址干扰，而差分跳频则是异频可能会形成多址干扰。因此差分跳频同步组网的概念应扩展为在同一张频率表的条件下，各跳频网每一跳的起跳时刻相同时，任一时刻各网瞬时频率不相互形成干扰。差分跳频图案是由随机数据信息控制G函数产生的，而每部电台和各跳频网的数据源是不同的，是相互独立的，相互之间不可能有某种约束关系，导致了即使各台及各网之间在时间上有约束关系，也难以实现各台各网之间频率的人工干预，这样一来，当接收方收到的频率为当前G函数映射出的除当前发送频率之外的m-1个频率中的某一个频点时，就会形成多址干扰。也就是说，要做到差分跳频各网当前跳变频率不落在其余网G函数映射的频率子集之内相当困难。需要通过研究G函数的算法，寻找适当的映射途径，使得各网跳变时刻相同，但任一时刻各网瞬时频率不相互形成多址干扰。

3 AWGN下差分跳频系统的多用户能力分析

图1为DFH多用户系统模型。每个发射机提供一种交织编码样式，这种编码的码型同数据比特流一起构成传输波形。在每个接收机处，解码器也使用与对应用户相同的码型。如果某接收机对多个发送信号感兴趣，它为合成信号中每个发送信号创建一种检测交织编码样式。其他的发送信号则被认为是干扰，而DFH解码算法能很好地抑制这些干扰。然而某些时候，在已经投入使用的DFH多用户系统中，用户数量会影响解码的性能，而且对干扰的消减程度也是适当的。

图1 DFH多用户系统示例

根据频率数、信噪比、产生一个DFH多用户系统的理论上的误码率γ，以及干扰的数量N-1,并使用多用户信干比SINR为γMU。

在DFH解码的每一阶段，干扰信号会造成模糊概率ρ=（2b-1）/M.换句话说，来自功率为S某一干扰信号的有效的干扰为ps=（2b-1）S/M.因此，如果存在N个功率相等的用户，每个用户都以与无干扰状态下的信噪比γ=S0/N相一致的信号电平来进行传送，这样就可以确定有效的信干比

γMU=γ/（1+γ（2b-1）（N-1）/M）      （1）

这样就可以得到高斯白噪声信道条件下的总用户数为N的DFH多用户系统的理论误码率为

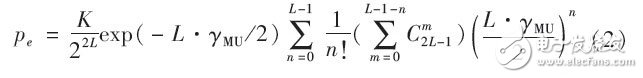
在用户数N=10,b=1的情况下，仿真信噪比随跳频频率个数的变化如图2所示。

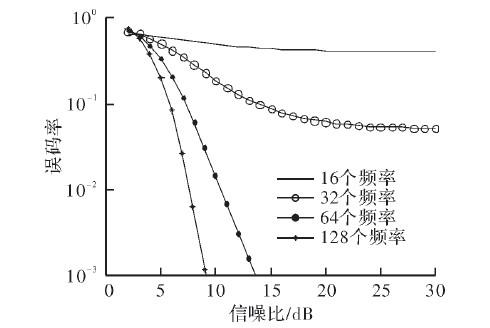
图2 M值不同的条件下DFH系统误码率随信噪比的变化

在图2中，画出了用户数为N=10,M=16、M=32、M=64、M=128的条件下，误码率随信噪比的变化曲线。由图可以看出，可用频点数M越高，误码率随信噪比的变化越快，且M越大，相应信噪比条件下的误码率越小，系统性能越好。

设定仿真参数，跳频频率个数M=64,b=1,用户数以2的指数增加，仿真如图3所示。

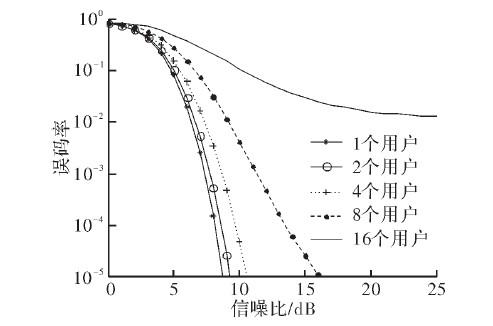
图3 DFH系统在用户数不同的情况下的误码率比较

在图3,中使用Matlab分别画出了用户数N=1、N=2、N=4、N=8、N=16时，DFH系统误码率随信噪比的变化图。由图可以看出，用户越多，DFH系统的误码率越大，信噪比曲线越平缓，即误码率随信噪比变化的速度较慢；用户越少误码率越小，信噪比曲线就越陡峭，即误码率随信噪比变化的速度较快；此外，系统用户数越少，在相应信噪比条件下误码率越小，说明干扰小。

4 结束语

讨论了差分跳频系统的多用户能力，并进行了仿真计算，得出了有益的结论，这将对差分跳频新体制进入实用化有一定的指导意义，为差分跳频组网问题提供了有益的参考，但差分跳频系统的多用户能力还有待于进一步研究，可将其与其他跳频技术的组网能力进行比较研究。