卷积码编码和维特比译码的原理、性能与仿真分析

1.引言

卷积码的编码器是由一个有k位输入、n位输出，且具有m位移位寄存器构成的有限状态的有记忆系统，通常称它为时序网络。编码器的整体约束长度为v,是所有k个移位寄存器的长度之和。具有这样的编码器的卷积码称作[n,k,v]卷积码。对于一个（n,1,v）编码器，约束长度v等于存储级数m.卷积码是由k个信息比特编码成n（n>k）比特的码组，编码出的n比特码组值不仅与当前码字中的k个信息比特值有关，而且与其前面v个码组中的v*k个信息比特值有关。

卷积码有三种译码方式：序列译码、门限译码和概率译码。其中，概率译码根据最大似然译码原理在所有可能路径中求取与接收路径最相似的一条路径，具有最佳的纠错性能，维特比译码是概率译码中极重要的一种方式。

序列译码和门限译码则不一定能找出与接收路径最相似的一条路径。不同于维特比译码，门限译码与序列译码所需的计算量是可变的且对于给定信息分组的最终判决仅仅基于（m+1）个接收分组，而不是基于整个接收序列。

与维特比译码所使用的对数似然量度不同，序列译码所使用的量度为Fano量度。在接收序列受扰严重的情况下，序列译码的计算量大于维特比译码所需的固定计算量，虽然序列译码要求的平均计算次数通常小于维特比译码。在采用并行处理的情况下，维特比译码的速度会优于序列译码。在同样码率和存储级数的条件下，门限译码的性能比维特比译码低大约3dB.

维特比译码的数据输出方式有硬判决及软判决两种方式，本文选取生成多项式为561,753的（2,1,8）卷积码对硬判决的性能进行分析，并依据维特比译码的原理以及卷积码的特性，对卷积码编码和维特比译码过程在加性高斯白噪声（AWGN）信道下进行仿真，并且根据仿真结果对维特比译码（硬判决）的结果进行分析。由于卷积码的生成可以看做一个马尔科夫过程，因此，不同状态间的转移概率对描述这个过程有极关键的作用。本文则基于MATLAB对不同状态间的转移概率进行求解，从而更准确地分析维特比译码的性能。仿真结果表明卷积码抗突发错误的能力不强，生成多项式为561,753的（2,1,8）卷积码在信噪比大于1dB时，编码增益体现明显。在信噪比低于-1dB时，编码增益得不到体现。

2.卷积码编码译码原理

卷积码编码通过输入序列与生成多项式的每一行做卷积，每次输入k比特，输出n个比特。在卷积码编码器中，每（m+1）个比特构成译码器中的一个状态。假设在一个二进制输入的离散无记忆信道上，有一个长度为k*L的信息序列u=（u0,u1,…，uL-1）被编码成为长为T=n（L+m）的码字c=（c0,c1,…，cT-1），接收到的序列为r=（r0,r1,…，rT-1）。维特比译码使用对数量度来衡量幸存路径所编成的码字与接收序列的相似度，量度越大，说明该幸存路径是信息序列的概率越大。维特比译码选取那条量度最大的幸存路径作为译码结果。

由于对离散无记忆信道：

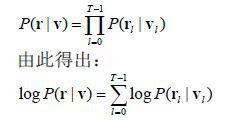
其中P （ r l | v l ）是信道转移概率；logP（r|v）称为和路径v相关的量度，以M（r|v）表示；logP（rl|vl）称为分支量度。

维特比译码的原理则是找出一条路径，使得该路径的累积量度最大。在译码过程中，如果在某一节点上发现某路径已不可能是需要找到的那条路径，就将此路径去掉，不保存在幸存路径之中。然后再在剩下的幸存路径中选择译码路径，直到输入所有译码器序列。理论上，搜索路径需要无限长度，而实际应用中考虑到试验因素搜索长度有限，搜索长度对译码性能有一定的影响，搜索路径的长度一般为约束长度的四倍到五倍。维特比译码可以被总结成如下步骤：

第一步：在时间单元t=m开始，计算进入每一状态的单个路径的部分量度，并存储每一状态下的路径（幸存的）及其量度。

第二步：t增加1.将进入每一状态的分支量度与前一时间单元有关的幸存路径的量度相加，计算进入该状态的所有2k路径的部分量度；对每一状态，比较进入该状态的所有2k路径的量度，选择具有最大量度的路径（幸存路径），存储该路径及其量度，并删除其他所有路径。

第三步： 如果t < L + m , 重复步骤二；否则停止。

维特比译码性能分析：

假设一个二进制序列经BPSK调制后通过加性高斯白噪声（AWGN）信道后的误比特率为e,因为本文采用的生成多项式为561,753的（2,1,8）卷积码编码器，则有9*2=18个比特与当前输出比特相关。由于该卷积码的自由距为12,因此如果一个比特出现译码错误，则留下的幸存路径（也即最大似然路径）经编码后的序列会与正确路径的序列相差1 2比特，并且会对其后18个比特产生影响。

所以，维特比译码抗突发错误能力不强，而实际应用时往往在卷积编码后加入交织编码，使突发错误离散化。因为卷积码的马尔科夫性，可以推测出：当不编码时，若误比特率足够高，则编码后序列的误比特率会比不编码更高。而仿真结果表明，当未编码序列的误比特率达到8*10-2,随着未编码序列的误比特率升高，编码后序列的误比特率会迅速升高。而在当未编码序列的误比特率小于5*10-2时，编码后序列的误比特率升高得较为缓慢且编码增益得到明显体现。

3.卷积码编码及维特比译码仿真

自编函数对维特比译码仿真：

本文应用MATLAB对卷积码编码器以及维特比译码器进行仿真。由于卷积码的马尔科夫性，转移概率是其中一个重要特性。显然，如果其中一个比特译码错误，后面N个比特的误比特率都会因此受到影响，所以需要求出一步转移概率、两步转移概率…N步转移概率。由于本文采用的是（2,1,8）卷积码，N=8.

基于MATLAB首先编写出模拟卷积码编码和维特比译码的函数，再分类讨论。在一定误比特率情况下，当影响第L个比特译码的2*9个比特中错n（n=1,2,3…，18）个时，求得第（L+N）比特译码错误的转移概率。假设BPSK调制的误码率为e;在影响第L比特译码结果的18个比特中有n个误比特时，假设第（L+h）个比特经译码后的误比特率为P （h） n .

由于加性高斯白噪声信道是非记忆信道，则译码后序列的误比特率近似等于：

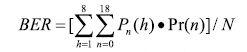
其中Pr（n）是18个比特中有n比特错的概率，当误比特率为e, ,N=18.

创建m文件，函数有三个输入：生成多项式G、接收到的信道输出误比特率BER、影响第x比特译码结果的18比特中的误比特数n,输出则是P （h） n .这里h的值为1~8.对于信道输出序列的误码率为0.1时进行分析，基于MATLAB仿真得到的所有P （h） n 如图1所示。

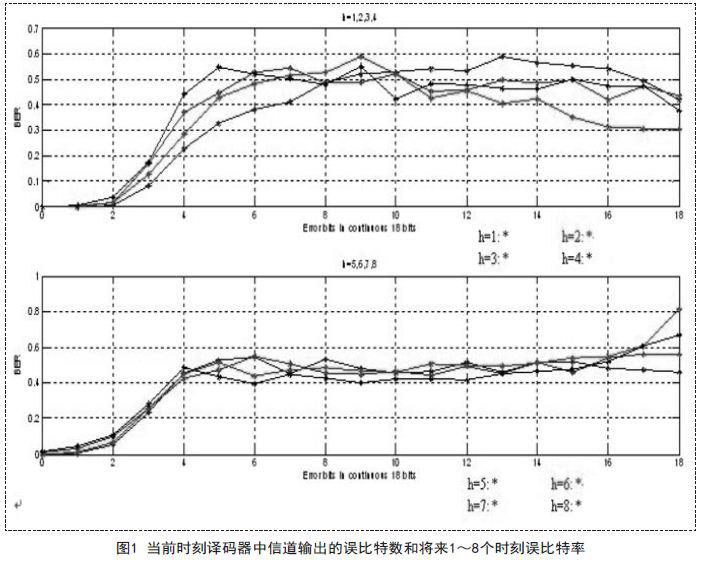
由图1中的结果可以算出当接收到的信道输出序列的误码率为0.1时，经维特比译码后的误比特率约为0.1071.

而且，当信道输出中连续1 8比特的误比特数大于3 时， 第（ x + h ） 个比特的误比特率远高于平均误比特率，这表明维特比译码抗突发错误能力低下。

以n=4为例，根据图1中数据可得出当h=1,2,…，8时，第（x+h）个比特的平均误比特率为0 . 3 9 2 2.当n的值比较小时（ n < 4 ），可以得到以下结论，当h=1,2,…，8时，第（x+h）个比特的误比特率随h增加而增大。由于卷积码的特性，第L个比特的译码结果可直接影响第（x+j）个比特（j=1,2,…，7）的译码结果，而第（x+j）个比特的译码结果又会直接影响第（x+h）个比特（h=1,2,…，8）的译码结果。因为这种迭代关系，第（x+h）个比特的误码率会随h增大而增大，从而造成卷积码抗突发错误性能低下。并且，在信道输出的误码率较大时，码字速率已经大于信道容量，此时采用编码不可能进行可靠通信。

仿真结果表明：当信噪比等于-1dB时，一个序列通过加性高斯白噪声信道后接收到的信道输出误比特率大于10-1,且该序列运用[2,1,8]卷积码编码，维特比译码（硬判决）后所得的序列误比特率升高。当信噪比为2dB时，一个序列通过加性高斯白噪声信道后接收到的信道输出误比特率约为4*10-2,且该序列运用[2,1,8]卷积码编码，维特比译码后所得的序列误比特率小于10-3,误码率远低于不编码时的误码率。因此卷积码适用于信道输出误码率比较低时候。

4.结论

本文基于MATLAB对卷积码编码和维特比译码进行仿真，比较了未编码序列的误比特率和编码后序列的误比特率。依据卷积码的马尔科夫性，利用MATLAB仿真，对其转移概率进行了求解，并通过转移概率得出了维特比译码的性能以及卷积码抗突发错误能力不高的结论。当信噪比为-1dB时，生成多项式为561,753的（2,1,8）卷积码的误码率约为1.27*10-1,而不编码的BPSK的误码率约为1.04*10-1,编码后误码率反而高于不编码。在信道条件较好时，卷积码的编码增益体现明显，当信噪比为2dB,生成多项式为561,753的（2,1,8）卷积码的误码率约为8*10-4,而不编码的BPSK的误码率约为4.64*10-2,编码后误码率明显降低。