应用于导航接收机中的抗混叠滤波器设计

引言

软件无线电是指以现代通信理论为基础,以数字信号处理为核心,以微电子技术为支撑的无线电技术。导航接收机主要是基于中频带通采样的软件无线电装置,它将射频信号先变为标准的中频信号,以适应A/D转换的需要,然后通过可编程数字信号处理模块进行中频数字化处理。采用软件无线电的思想来实现导航接收机终端具有灵活性、集中和模块化三个优点。

导航接收机作为一个软件无线电系统,需要处理多种速率的信号。如果为每种速率配备一个专用主时钟,系统就会变得既昂贵又缺乏灵活性。事实上,也可以只用一个主时钟,即对所有的信号都用一个固定频率进行带通抽样,然后通过抽样速率变换技术来得到不同标准的比特或码片速率。

SRC可以通过内插和抽取等组合方式来计算离散时间信号中的某些值,从而获得特定频段内的信号。在软件无线电中,用Farrow结构实现的基于分段多项式脉冲响应的滤波器结构类似于FIR结构,它具有固定的乘法器系数,同时具有可变数字延时单元,而且可以通过调整数字延时来改变频率转换的比例,因而是实现抽样速率变换的一个比较好的选择。

1 Farrow滤波器的设计

1.1 抗混叠滤波器设计

SRC可以看作是对一个重建信号的再抽样。即通过对数字信号进行数模转换和滤波来得到一个模拟信号,然后再对这个信号进行抽样处理。图1所示是其重建信号再抽样示意图。

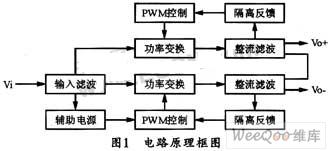
图1中,L为内插因子,M为抽取因子,两者都是正整数,且L和M互质。SRC因子可用L/M或T2/T1的比值来表示。这里的T1是第一次抽样后的周期,而T2则是经过内插和抽取后的周期。T1和T2有如下关系:

对一个信号的内插会引起频谱的镜像,而抽取则会引起频谱的混叠。其中,频谱混叠将会破坏信号,因此,抗混叠是SRC最需要关注的。SRC的主要任务就是设计满足要求的重建滤波器以满足抗混叠要求。

图1中的SRC滤波和再抽样表达式如下：

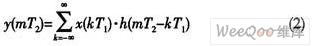
(2)式是在滤波器h(t)的连续时间冲击响应抽样和输入信号x(kT1)之间的一个类似卷积的操作,该操作会使输出信号y(mT2)产生一个新的速率。每计算一个输出抽样都要用到h(t)冲击响应的抽样值。而由于h(t)冲击响应的抽样值与T1,T2,k和m有关,不同时间是不一样的。因此,需要知道滤波器h(t)的连续时间冲击响应,而不是一些特定的抽样值。式(2)实际上是一个时变系统。h(t)可以看作是一个在时变离散系统中的连续时间滤波器。

对有理数和整数因子的SRC系统,h(t)是周期时变的。因此,处理时只需要计算h(t)的一些特定抽样值。这些值可以预先存储起来,以用于典型的有理数SRC系统。

对于SRC因子是无理数的情况,可以用一个有理数来近似表示。但是,当L和M很大时,往往需要很大的存储空间,这种方法就不实用。因此,必须找到一种更好的方法,以根据需要计算任意因子SRC的h(t)抽样值。

为了减少计算h(t)抽样值的工作量,可以用分段多项式函数来表示h(t):

式中,N为级联多项式的数目,Δ为分段多项式的长度。pj(t)表示第j段分段长度为Δ的多项式。j=「t/Δ」,「」表示取整操作。这样,只需要确定采用何种滤波器以及输入和输出抽样速率,就可计算出表示该滤波器的多项式的系数。用该方法计算每个输出抽样值所需要的计算量很小。这种方式可看作是在已有冲击响应基础上的内插冲击响应,即利用多项式及其系数来计算新值。分段多项式的阶数越高,h(t)就越能反映实际情况。但阶数过高会引起系统的不稳定。通过降低阶数并减小分段长度可以保持滤波器的精度。这样,(3)式又可以表示为:

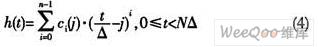
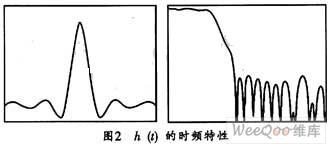
这里的ci(j)表示多项式pj(t)的第i阶系数,n-1表示多项式的最高系数。一旦确定了SRC因子和多项式,就可以求出滤波器系数。Δ的大小是一个很重要的问题。不同的会使滤波器具有不同的抗镜像和抗混叠性能。设h(t)频域响应可用一个滚降因子r=0.22的截断升余弦函数表示,其冲击响应长度为10·Δ。分段多项式可用最高阶数为3的样条函数表示,其时频特性如图2所示。图中的主瓣比第一旁瓣高36.7dB,可见其有很好的抗混叠或抗镜像性能。

1.2 Farrow滤波器的原理结构

把(4)式代入(2)式,并令Δ=T1,可得:

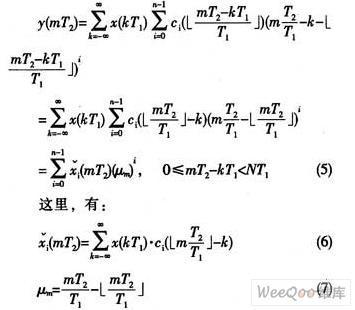
其中,μm表示当前输出抽样点与其前面输入抽样点之间的距离,且有0≤μm<1。由(5)式即可得出一种实现SRC滤波的多项式滤波器,一般称为Farrow结构,该结构的联络图如图3所示。对于距离原来抽样位置为μm的任何输出抽样值,若用t=μm代入所在位置的分段多项式就可以计算出来,而不需要存储这些抽样值。图3中的ctrl(mT2)表示周期为T2的控制抽取脉冲。

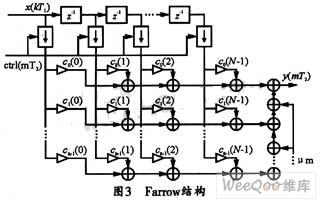
从上面的分析可以看出,Farrow结构以内插、多项式滤波和抽取操作级联的方式来实现任意因子的SRC,它涉及到三种速率,即输入速率1/T1、内插后的速率L/T1以及抽取后的速率1/T2。当L很大时,内插后的速率L/T1会很高,往往达到千兆级,这显然对器件的运算能力提出了极高的要求。但实际上,内插点的值除在L的整数倍上以外都是零。因此,在设计滤波器时,内插只在理论上产生影响,实际上可以不执行内插操作。这样就降低了Farrow结构对器件处理能力的要求。

对Farrow结构来说,Δ=T1,本质上就是一个用多项式实现的、后面有抽取器的多相内插滤波器。它的传输零点集中在输入抽样速率1/T1的整数倍上,因此,其抗镜像性能比较好,而抗混叠性能不理想。如果令Δ=T2,则可得到一种称作转置Farrow的结构,这本质上是一个用多项式实现的、前面是内插器的多相抽取滤波器,它的传输零点集中在输出抽样速率1/T2的整数倍上。它具有良好的抗混叠性能。而抗混叠是SRC主要关注的性能。

2 Farrow滤波器的FPGA实现

2.1 模块化设计

模块化的设计思想是将大规模复杂系统按照一定的规则划分成若干模块,然后对每个模块进行设计输入、综合,并将实现结果约束在预先设置好的区域内,最后再将所有模块的实现结果有机的组织起来,从而完成整个系统的设计。

模块设计常用的设计输入方式为框图与HDL语言设计输入方式。顶层模块用于描述全局逻辑,主要包括设计的输入/输出、端口描述与信号属性声明、以及子模块之间的连接关系。子模块的设计通常也使用框图与HDL语言输入方式。

基于这种抗混叠滤波器设计和Farrow结构,可对实现抽取滤波器的滤波进行模块化设计。图4为Farrow模块顶层原理图。该模块包括延时子模块、多项式滤波子模块和Mu值乘法子模块等。

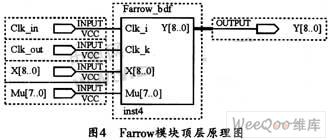
2.2仿真

在选用软件调试时,可采用QuartusII5.0软件,它支持Altera公司的大部分CPLD及FPGA芯片,可以降低设计和校验周期,提高设计效率。QuartusII5.0内含实时调试工具,并带有含有逻辑锁定功能,可使模块化设计达到最优化的设计效果。此外,它还含有将FPGA设计向ASIC设计无缝转移的高效的ASIC设计技术。QuartusⅡ的RTLViewer(寄存器层查看器)还提供了一个可以看到低层逻辑电路,并对其进行分析和节点定位的功能,从而极大的方便了程序的调试。因此,本文采用QuartusII来编译仿真。

该仿真的输入时钟Clk_in为50MHz,输出时钟Clk_out为25MHz。X[8..0]为输入数字信号,时间间隔为1/50MHz,另外,在仿真时还假定Mu[7..0]为固定值,Y为经过抽取滤波器后的输出值,时间间隔为1/25MHz。仿真结果证明:该设计完全可以实现抽样率由50MHz降为25MHz的速率转换。

2.3芯片选型和验证

本导航接收机整个基带处理模块选用Altera公司Stratix系列的EP1S25F672C7芯片。该芯片采用1.5V内核,0.13um工艺,含有25660个逻辑单元,内嵌三种RAM块(M512,M4K,MRAM),RAM总容量为16KB,引脚为672个,最大可用I/O引脚为582个。经过编译,该滤波器仅占用305个逻辑单元,占整个逻辑芯片资源的2%。通过ByteBlasterMV下载电缆适配程序到FPGA中进行测试证明。其测试结果完全满足设计要求。

3结束语

本文讨论了在导航接收机中采用软件无线电技术进行抽样速率变换的抗混叠滤波器的设计方法,采用该方法设计的基于Farrow结构的抽取滤波器,可以成功地运用于导航接收机位定时调整电路中。