

基于FPGA实现AES算法数据加密方案
描述
1. 引言
随着国际空间任务交叉合作增加,应用地面公共数据网络进行空间任务控制和数据监测越来越多,空间飞行器迫切需要数据安全保护机制。随着计算机技术的迅速发展,原 来卫星(如SPOT 卫星)上使用的DES 加密算法已能够被穷举法破译。为此,美国国家标准 和技术协会(NIST)于2000 年10 月2 日宣布采用Rijndael 作为下一代先进加密标准(AES) 的正式算法[2]。2004 年,CCSDS(国际空间数据系统咨询委员会)建议将AES 作为空间 数据加密算法标准[3][4]。目前,AES 加密算法已在NASA、FBI、CCSDS 等机构得到广泛 应用。
随着我国空间技术的快速发展,未来需要考虑空间数据安全性设计。传统的星上加密 需要一个专门的装置,占用的体积、功耗等资源均较大。AES 算法适用于软硬件资源有限 的应用中,同时与软件加密相比,采用FPGA 进行物理加密具有很好的防攻击性,实时性好, 可实现高速数据处理,资源占用非常小,是空间数据加密的重要发展方向。
本文对AES 算法进行了研究,并在一片FPGA 上进行了仿真分析,确定了适合空间应 用的AES 算法。
2. AES 加密算法及优化实现
2.1. AES 加密算法
AES 是一种可变密钥长度的迭代分组加密算法,明文被分成以128bit 为一块进行加密, 密钥长度可分别为128bit、192bit、256bit。
AES 加密算法包括密钥扩展过程和加密过程。加密过程又包括一个作为初始轮的初始密钥加法(AddRoundKey),接着进行若干次轮变换(Round),最后再使用一个轮变换(FinalRound),如图2.1.1 所示。

明文可以表示为4*4B 的状态矩阵,加密的每一轮是对状态矩阵进行操作,得到中间结 果状态矩阵。初始变换指的是状态矩阵中每一列与初始密钥进行加运算。轮变换的每一轮 包括字节替换(SubBytes)、行移位(Shiftrows)、列混合(Mixcolumns)、轮密钥加 (AddRoundKey)。最后一轮变换不包括列混合(Mixcolumns)。经过最后一轮变换,中间状 态矩阵将输出4*4B 的密文。
密钥扩展是对给定初始密钥进行运算,得到每个轮变换的轮密钥。主要包括三步:字 替换(Subword)、周期置换(Rotword)、圈常数字序列加运算[2]。AES-128 与AES-192 密 钥扩展的每一轮都包括三个步骤,对于AES-256,并不是每一轮都包括三个步骤,当密钥 替换循环次数小于Nb*(Nr+1)(Nb 数据块长度、Nr 圈数),同时循环次数对Nk(密钥长度) 取模的结果为4 时,只进行字替换(Subword)。
表 2.1.1 给出了三种AES 加密的明文块长度,密钥长度,加密轮变换次数之间的关系。
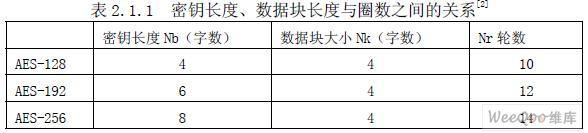
2.2. AES 算法优化实现
2.2.1. 字节替换(SubBytes)
SubBytes 主要通过两步来完成,一步是在GF(28)中取乘法逆,另外一步是通过特别 定义的GF(2)上的仿射作用。为了避免复杂的乘法运算,在FPGA 上具体实现时,构造了 16*16B 的置换表,通过查表完成了字节替换,节省了运算时间。
2.2.2. 行移变换(shiftrows)
ShiftRows 与列混合运算相互影响,在多轮变换后,使密码信息达到充分的混乱。行变 换是在状态的每个行间进行的,是状态中的行按不同的偏移量进行循环左移运算[10]。通过 对每个字节的行移位实现该变换。
2.2.3. 列混合(MixColumns)
假设列混合运算输入为a,输出为b,加密的列混合运算可做如下表示:

式2.1 所示的矩阵运算是伽罗华域上常数乘法运算。伽罗华域上乘以任何常数的乘法 都可以通过反复的乘以02 和异或运算来实现[5]。将GF(28)域中的每一个元素与02 的乘积 存储在一张16*16 B 查找表中,通过异或运算和查表即可实现列混合运算。
2.2.4. 密钥加法(AddRoundKey)
AddRoundKey 是将轮密钥中的各个字节与状态中的各个字节进行逐位异或运算,实现 密码和密钥的混合。轮密钥是由初始密钥通过密钥扩展得到的。
2.2.5. 密钥扩展(KeyExpansion)
初始密钥和扩展后的整个密钥表可以看作是一个字(word)序列。密钥扩展是针对字进 行的,为此又引入了两个对字进行处理的函数:字替代(Subword)和字旋转(RotWord)。字 旋转将字的4 个字节循环右移一个单位。密钥扩展还包括引入轮常数Rcon。字替换和引入 轮常数均可使用查表法完成。字旋转可以用简单的交换字的顺序实现。
在FPGA 的实现过程中,若不进行上述诸如查表法的优化,将会造成资源占用过度,运 行速率低下的情况。 3. AES 算法实现与仿真
3.1. AES 算法实现方案
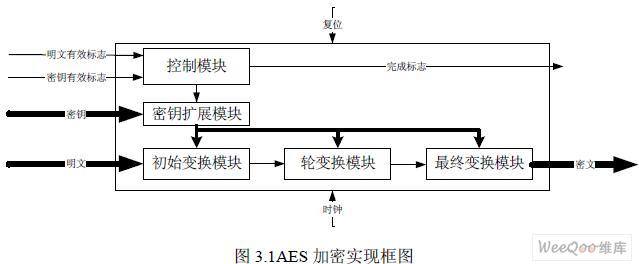
图3.1 为AES 加密算法实现框图,其中明文有效标志和密钥有效标志输入给控制模块, 初始密钥送给密钥扩展模块,明文输入到初始变换模块。控制模块输出加密完成标志,最 终变换模块输出密文[7]。其中粗箭头为数据线,细箭头为控制线。为满足加密过程的时序 要求,控制模块对输入的明文有效信号及密钥有效信号进行控制。密钥扩展模块在不同轮 数下产生的扩展密钥分别送给初始变换模块,轮变换模块以及最终变换模块。初始变换模 块对明文加了初始轮密钥;轮变换模块进行了四个变换步骤。最终变换模块与轮变换模块 不同在于没有进行混合列操作。
3.2. 仿真结果
本设计采用VHDL 语言,在Xilinx 公司的一款FPGA 上实现了AES 算法。分别对AES-128、 AES-192、AES-256 加密算法实现进行仿真,在FPGA 资源占用率、数据处理速率等方面进 行了对比分析。
(1) 仿真结果
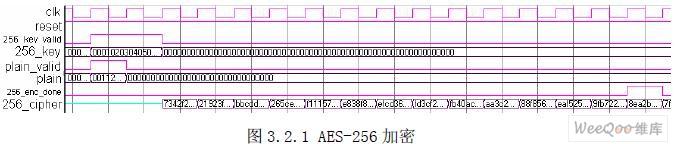
图3.2.1、3.2.2、3.2.3 分别是AES-256、AES-192、AES-128 的FPGA 实现仿真结果, 从图中可以看出AES-256 可以在15 个时钟周期内完成,AES-192 可以在13 个周期实现加 密算法,AES-128 可以在12 个时钟周期内实现加密算法。

(2) 性能分析
在Xilinx 公司的一款X2V 系列FPGA 上所占用的资源情况对比如表3.1.1。
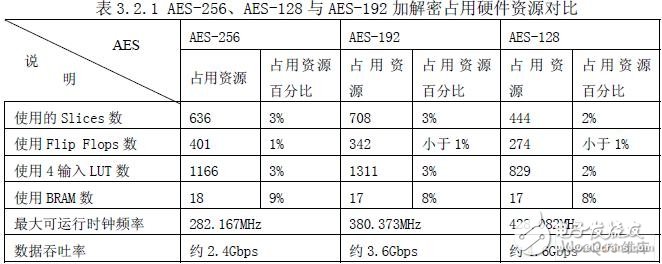
根据密码学理论,密钥长度越长,其安全性能越好。AES-256 占用硬件资源较AES-128、 AES-192 多,但AES-256 可以提供最好的安全性。三种加密算法占用的资源数相当,数据 吞吐率随着密钥长度加长而变小。
4. 结论
本文对AES 算法进行了研究,提出了面向空间应用的AES 算法的FPGA 实现方案。通过 仿真分析,表明利用FPGA 进行AES 进行数据加密具有占用硬件资源较少,数据吞吐率高, 安全性好的特点,门数在10 万左右的小型FPGA 即可实现该算法。考虑到安全性,在实际 应用中,AES-256 算法是最适合的。
-
aes加密的常见错误及解决方案2024-11-14 5427
-
最强加密算法?AES加密算法的Matlab和Verilog实现 精选资料推荐2021-07-28 1884
-
使用FPGA实现类AES分组密码统一框架的详细资料说明2021-03-26 863
-
如何低成本实现AES密码算法的硬件2020-03-19 1326
-
使用FPGA实现AES算法的优化设计2019-04-18 4138
-
用matlab实现AES加密算法2018-05-25 2297
-
AES加密算法说明2017-11-30 2690
-
有木有知道使用RSA算法数据加密滴?2015-11-26 6285
-
基于AES算法的加密模块设计2013-02-21 1369
-
【FPGA参赛作品】基于FPGA的AES分组加密系统2012-06-12 4417
-
基于AES和ECC的混合加密系统的设计2012-03-20 1577
-
基于FPGA加密芯片的DPA实现与防御研究2011-12-05 1284
-
基于FPGA的AES加密算法的高速实现2010-01-25 779
-
基于AES算法的无线加密数字传输系统2010-01-22 730
全部0条评论

快来发表一下你的评论吧 !

