深度解析混频器群时延

在聊混频器群时延之前，我们先聊一聊群时延。

在射频微波领域，群时延是一个经常可以看到的概念，它表示电磁波通过一个器件或者说一个系统的传输时间。对于信号传输来说，这个概念非常重要。单一的连续波信号是无法传输信息的。能传递信息的一定是由不同频率分量组成的一个“群”信号。如果这个群中各个频率分量的信号通过一个系统的时间不一样，那么这个系统输出的信号群包络就会发生畸变。这有点像田径比赛中的百米飞人大战：在起跑线上，大家排成一排，整整齐齐的;到了终点冲线的时候就变成有先有后，队形全乱套了。对于百米飞人大战，这样的结果当然是让人心潮澎湃，非常过瘾。但要是信号也是这样，那对通信系统来说可是大大的不妙。我们希望所有人到终点时还能保持队形，就像阅兵式上，方队中每个人的速度都一致，在起点和终点，方队的队形也是一样的。

我们看一下图1的例子：输入信号有三个频率分量(红线)，频率分别是基波频率fo，二次谐波频率2fo和三次谐波频率3fo，他们组成的信号包络(蓝线)近似于一个方波。再来看输出信号，由于这三个频率的传输速度不一样，在输出端，频率还是这三个频率，但包络已经发生了严重的畸变。这样的畸变会给通讯系统带来很多麻烦。

 

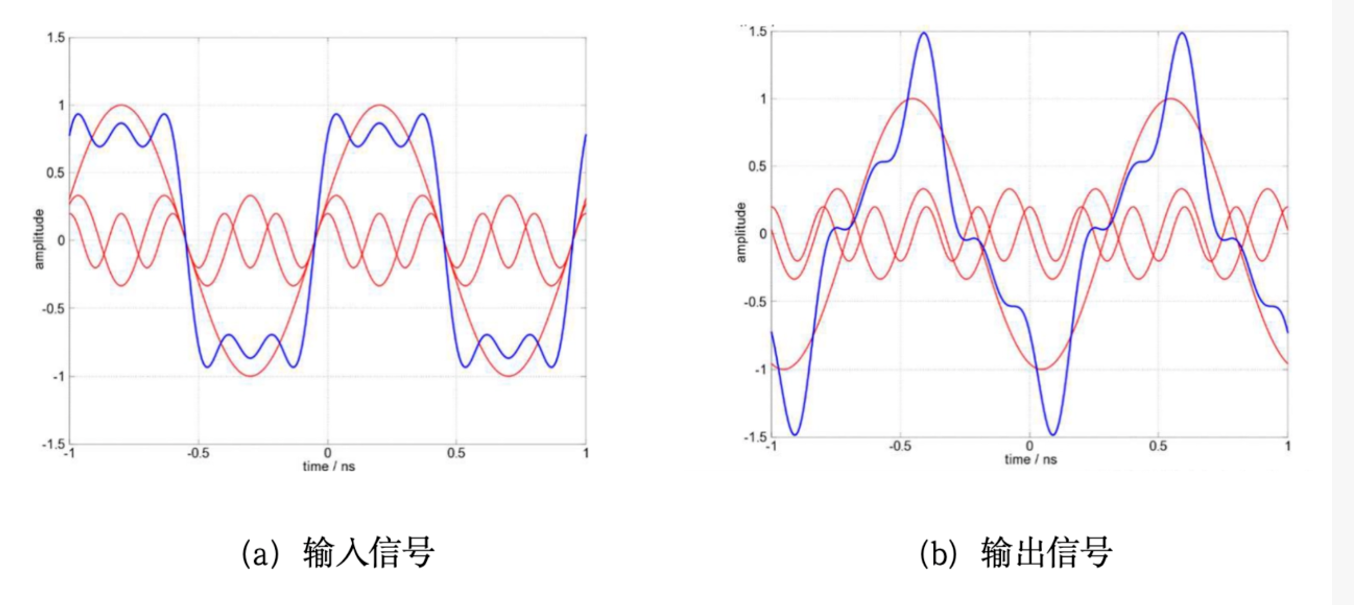
图1一个方波信号，因为不同频率传输的速度不一致，信号发生了畸变

一个理想的传输系统，我们希望输出的信号包络和输人的信号包络是一致的，这样的系统我们称为无失真传输系统。在《信号与系统》这门课上我们学过，一个无失真传输系统需要满足两个条件：

·系统的幅频特性在整个频域范围内应为常数

·系统的相频特性在整个频率范围内群时延恒定

翻译成“人话”就是：

·对于信号中所有的频率分量，要放大就都放大相同的倍数：要衰减也都衰减相同的倍数，别有的大有的小。

·对于信号中所有的频率分量，通过系统的时间要一致，别有的快有的慢。所以，我们需要测量每个频率分量通过系统的时间，也就是该频率的群时延Tg。

Tg是一个实数，几乎所有的教科书上都是直接给出了它的定义式：

 

 

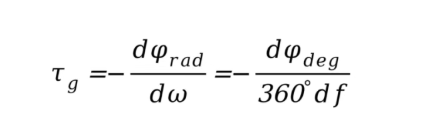
不知道小伙伴们怎么样，反正当初的我看到这个定义式是一头雾水：为啥相位对频率的微分就是群时延？为了更好的理解这个定义式，我们从一个例子人手。还是图1中的例子，要想知道信号包络是否发生了畸变，就要分别测出fo、2fo和3fo的群时延，然后看它们是否相等。先来测量fo的群时延。假设我们的被测件是一段同轴线，该如何测量呢?

反正我能想到的最简单的办法是直接掏出卷尺，把同轴线授直了量长度，然后根据同轴线填充介质的介电常数，计算fo信号在这根线中的传输速度，然后做个除法。从原理上来看，这种方法似乎没问题，但是工程上问题很大：首先用尺子测量长度的精度(更准确的表述是测量不确定度)很差，再加上介电常数的不确定度也很差，所以这种方法的精度并不高。更何况被测件往往不是均匀的，还需要分段计算。

第二种方法要高大上很多：将调制后的fo信号输入把被测件，然后测量输人输出信号包络的时间差，就可以测量出传输时间。

从原理上看也没问题，而且这样调制后的信号包络，更符合“群”的概念。早期的工程师也确实是这么测的，缺点就是这个系统搭起来略显复杂，我们在后面会讨论一种类似的方法。

熟悉矢量网络分析仪的小伙伴还会想到时域测试的方法。确实，无论是使用时域反射(TDR)还是时域传输(TDT)，都可以进行这个测量，但同样存在问题：矢量网络分析仪的时域测量精度(时域分辨率)跟测量的最高工作频率有关，最高工作频率越高，时域分辨率越高，如果测量一个窄带器件，这种方法的精度并不高。更重要的是，我们测得的这个时间，严格的说是所有频率分量构成的信号包络的传输时间，而不是我们想知道的某个特定频率fo信号的传输时间。

所以我们最终还是回到相位测量上来。首先我们假设信号通过这段同轴线的时间，也就是群时延为Tg，而对于频率为fo的电磁波，一个周期为To=1/fo。知道了时延Tg，就可以计算出这段同轴线上传输时经过了多少个周期，也就能计算出输入输出信号的相位差。比如对于fo=1GHz的电磁波，其周期为1ns；如果被测同轴线的群时延Tg=0.25ns，那么可以计算出在这段同轴线上有1/4个周期，也就是输出信号的相位会比输人信号的相位延迟90°，S21的相位为-90°。所以，如果已知了Tg，是可以准确的计算出S21的相位的。那么反过来，如果用矢量网络分析仪测量到了S21的相位，能否计算出群时延Tg呢？没那么简单。熟悉矢量网络分析仪的同学都知道，S参数的相位测量都存在360°的模糊，即使是非折叠相位(Unwrap phase)也不例外。也就是说S21的相位测量值如果是-90°，那么其真正的相位有可能是-90°、-450°、-810°…….，由此计算出来的时延Tg分别为0.25ns、1.25ns、2.25ns…。因此，如果我们只测量一个频点的相位是无法得到准确的时延Tg的。

我们再用跑步做例子，只不过从刚才的百米飞人大战变成了长跑。一个运动员沿着标准的四百米跑道，以恒定的速度跑步。如果我们没有从头看比赛，仅仅根据他现在的位置，是无法知道他已经跑了多少圈的(距离模糊)，也就无法知道他跑了多长时间。如何解决呢?既然一个人跑会出现距离模糊，那我们就给他加一个小伙伴。四百米的田径场上有多条跑道，由于圆周的关系，每条跑道一圈的长度并不相等。最内圈的跑道一圈是400米，相邻的第二条跑道一圈就是405米(并不准确，大家领会精神)。我们让两个运动员同时出发，以相同的速度跑，一个沿着400米一圈的跑道跑，另一个人沿着405米一圈的跑道跑。那么只要圈数不是特别多，我们就可以通过他们两的位置差来准确的判断出他们已经跑了几圈，从而解决了距离模糊的问题。

我们再回到群时延的测试中。同理，既然只测一个频点f1无法解决相位模糊，那我们也给它加一个小伙伴f2，只要这个小伙伴的频率跟他的频率差足够小，我们就可以认为他们的群时延Tg是一样的(两个运动员的速度是一样的)。频率不一样对应了他们的周期不一样(一个每圈400米，另一个每圈405米)，所以我们会得到两个不同的S21相位S211和S212，根据S21相位的相位差△和频率差△f，我们就可以解决相位模糊问题，准确的计算出群时延Tg了。详细的推导在附录A中，没兴趣的小伙伴直接忽略就好。

严格的说，对于色散(不同频率的电磁波传播速度不相等)的系统，f1的时延Tg1并不等于f2的时延Tg2。我们用这种方法计算得到的时延实际上是Tg1和Tg2的平均值。在定义式中，为了数学上的严谨，让f1与f2的频率差△f→0，于是相位差△p变成了dp，而频率差△f变成了df。但这也给当年的我带来了很大的困惑：既然这个时延是单一频点的时延，为啥要叫“群”时延呢?从上面的过程可以看出，单一的频点是无法通过相位的方法测出时延的，一定要有至少一个额外的频点跟它一起构成“群”后，才能测出这个信号群的平均时延。我们把它定义为这个频点时延，是数学上取△f→0的结果。小伙伴们也可以这样理解：一个频率点的“群时延”是以这个频率为中心的一个无穷窄带信号构成的“群”的时延。显然在工程上是无法测得这个严格数学意义上的群时延的，工程上是使用两个相邻的频点来计算群时延。这个频率差△f不能太大，否则会使相位差△p超过180°，再次出现模糊。有时候群时延会测出负值，那很可能就是△f太大引起的。工程上一般要求选取的△f对应的I△pl≤45°。测试前，应该估算一下被测件的群时延，然后可以根据附录B中的公式来计算△f的最大值。如果无法估计被测件的群时延，我们可以尝试用不同的△f来测试，看看群时延结果有没有巨大的变化。

△f也不是越小越好，相位测量也是有不确定度的。△f越小，群时延的不确定度就越大。举个例子，△f=1MHz时△=18°±0.5°，计算出来的群时延Tg=50±1.4ns；而△f=2MHz时△p=36°±0.5°，计算出来的群时延Tg=50±0.7ns。可以看出，相同的相位差不确定度条件下，△f越小，群时延的不确定度就越大。实际测试中也是这样，△f太小时，群时延曲线的噪声就比较大。

工程上通常使用矢量网络分析仪来测量群时延，R&S公司全系列的矢量网络分析仪都标配了群时延测试功能。矢量网络分析仪通过扫频，测量S21的相位，再通过相邻点的相位差和频率差计算群时延。在这个过程中，矢量网络分析仪是在一些离散的频点上进行测量的，线性扫频时频点的间距，也就是频率步长fstep可由下试计算。
 

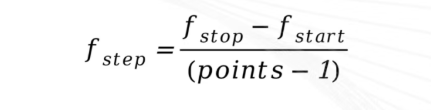
式中fstart为扫描的起始频率，fstop为扫描的终止频率，points为扫描点数。

除此之外还有一个参数“Aperture”(孔径)，这个参数用于调整△f的大小，Aperture就是告诉矢量网络分析仪，计算群时延时，△f应为频率步长(fstep)的几倍，即△f=Aperture×fstep°。
 

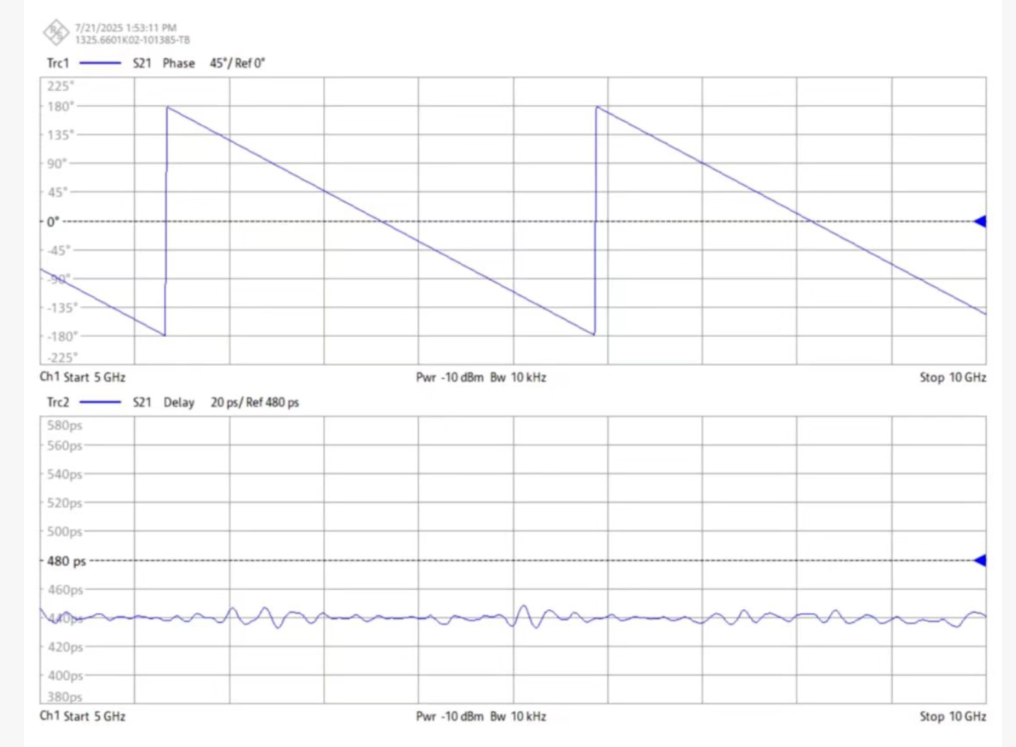
图2矢量网络分析仪测量S21的相位和群时延

除了使用矢量网络分析仪，信号源和频谱分析仪也能测量。R&SFSW提供了“多载波群时延测量”选件(R&SFSW-K17)。它的测试原理是由矢量信号源产生多个载波信号，载波信号的间隔就是Af，然后利用频谱分析仪测量输入的多载波信号相位差和输出的多载波相位差，来计算群时延。这个方法跟前面说的，用调制信号来测量群时延很类似，只不过不是直接测量信号包络的时间差，而是测量多载波之间的相位差。

技术细节可以参考应用手册：《Group Delay measurements with Signaland Spectrum Analyzers》
 

 

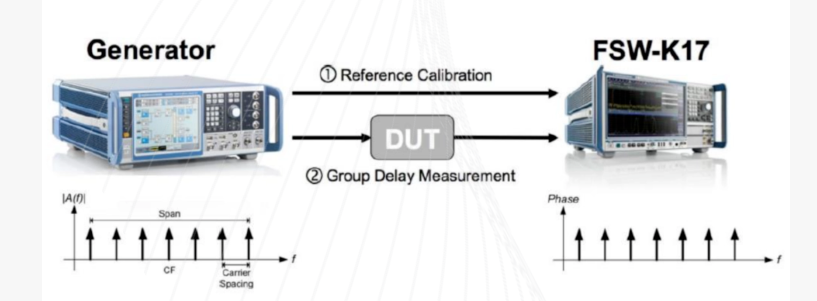
图3R&SFSW-K17多载波群时延测量

总结一下：

·一个频率的群时延Tg是该频率下传输系数相位相对于频率的变化率(导数)。

·一个频率的群时延Tg反映了以该频点为中心的无穷窄带宽内信号“群”包络通过被测件所需要的时间。

·一个频段内的群时延变化反映了被测件的相频响应是否是线性的，一个理想的线性器件，相频响应是线性的，也就是群时延Tg恒定。

·群时延可以通过扫频测量相位的方法得到，也可以通过比较双/多载波信号的相位得到。

现在让我们回到本文的标题：聊一聊混频器群时延。

混频器大家都很熟悉，现代的无线接收机中几乎都少不了混频器，它负责把射频信号搬移到中频。对于接收机来说，信号是从射频(RF)端口输入，从中频(IF)端口输出的。

很显然，从信号进入RF端口，再从IF端口输出，一定是需要时间的。我们要聊的混频器群时延就是指这个时间。之前讨论的信号无失真传输条件，对于混频器也同样适用。要想信号无失真的通过混频器，混频器的群时延在信号频带内也应该恒定。

有了之前的基础，我们很容易想到，可以用RF→IF的变频相位的导数(斜率)来计算混频器的群时延Tg。但是由于混频器的输入输出信号的频率是不同的，要比较RF一IF的变频相位，我们必须明确比较的时间点。这就要求矢量网络分析仪的射频源和本振源是相位相关的。在R&SZNA系列矢量网络分析仪中，采用了DDS(直接数字频综)作为参考源，可以保证矢量网络分析仪多个射频源以及内部接收机的本振源在不同频率上的实现相位相关。

需要注意的是，从RF端口到IF的变频相位还与本振(LO)信号的有关，LO信号的频率和相位一旦发生变化，整个信道(从RF端口到IF端口)的状态都会发生变化，因此在测量混频器的群时延时，需要固定LO信号频率，扫描RF信号频率和IF信号频率来测量。

通过测量变频相位的方法来测量混频器的群时延，由于f1和f2信号是在不同时刻输人被测件的，我们不仅要固定住混频器LO信号的频率，还要保证这个LO信号与输人混频器的RF信号始终相位相关。否则，LO信号在这两个时刻的相位抖动，会造成群时延的结果失去意义。这就要求被测混频器的RF信号和LO信号都由R&SZNA矢量网络分析仪提供。
 

 

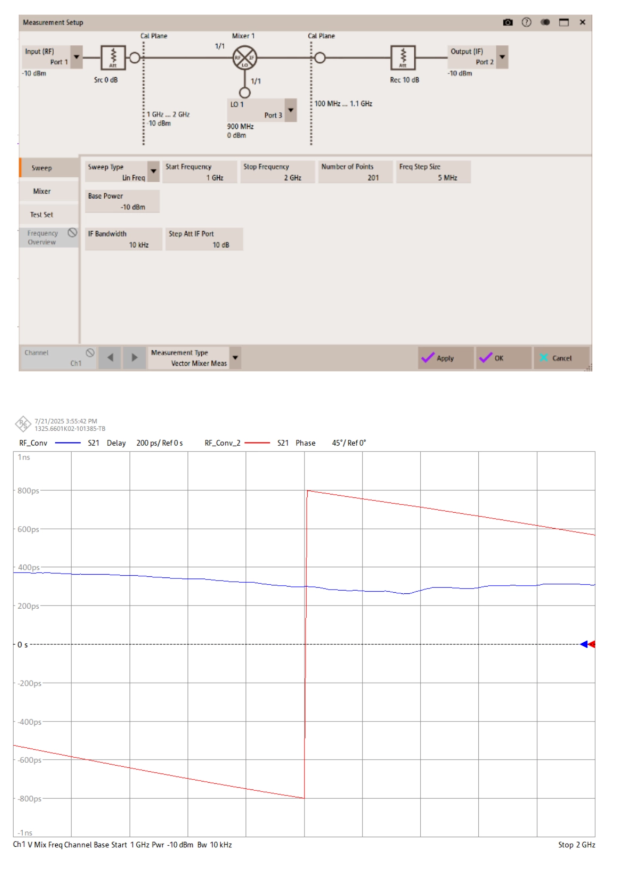
图4使用R&SZNA-K5、R&SZNA-K6选件测量变频相位和时延

很多被测混频器的LO信号是内嵌的，并没有外部LO信号的输人接口。此时，由于LO信号无法与射频信号相位相关，上述的方法是不能使用的。针对这一类的测试，可以使用“内嵌本振变频器时延测试”选件(R&SZNA-K9)。这种方法的基本思路是：既然混频器LO信号的相位不可控，我们就把它的影响抵消掉。在前面的扫频方法中，两个不同频率的RF信号是在不同时刻输入的，需要严格控制LO信号的相位；而使用R&SZNA-K9方法时，两个不同频率的RF信号同时输入，LO信号的相位抖动对这个RF信号的影响是一致的在计算相位差时，LO信号的相位影响被抵消掉了。我们分别测量出两个RF信号的相位差△RF=RF1-RF2和两个IF信号的相位差△IF=IF1-IF2，就可以得到变相相位的相位差△。再计算变频的群时延就简单了。这两个RF信号的频率差就是Af。这种测试方法实际上就是我们之前提到的双/多载波信号的测试方法。更详细的理论推导可以参考R&S的应用手册《Group Delay Measurement on Frequency Converting Devices》。

这个测试至少需要同时产生两个激励信号，因此矢量网络分析仪至少有两个独立可控的射频源，同时为了简化测试系统，需要在矢量网络分析仪中内置信号合路器，R&SZNA矢量网络分析仪提供了所有需要的选件。当然，没有内置合路器选件时使用外置合路器也是可以的。

需要说明的是，采用这种方法测量变频群时延时，需要一个已知群时延的混频器用于校准。通常是找一个可以外接LO信号的混频器，先用R&S ZNA-K5方法测量其群时延，再用这个混频器校准系统。

讨论了半天群时延以及混频器群时延，也不知道我给大家讲清楚了没有。如果各位小伙伴还有问题，欢迎和我们讨论，也欢迎咨询R&S公司的应用工程师。

附录A：群时延公式的推导

电磁波的频率f表示一秒钟会振荡多少个周期，时延Tg乘以频率f就可以得到输出信号比输入信号延迟了多少周期。由于有每延迟一个周期相位延迟360°，所以Tg×f×-360°就可以计算出输出信号延迟的相位。

我们考虑有两个不同频率的电磁波，频率分别为f1和f2，它们的时延Tg是一样的(未知)，我们分别测量出这两个频率下S21的相位S211和S212，可以得到：

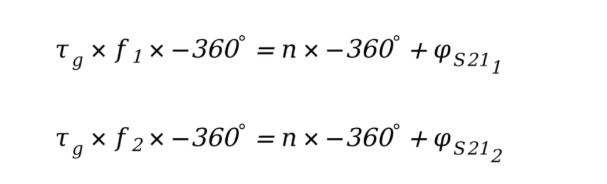
两个式子减一下，就可以得到：
 

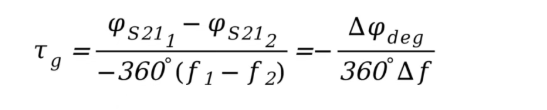
举个例子：我们已经测得了f1=1GHz(周期T=1ns)处S21的相位为-90°，可能的时延Tg有：0.25ns、1.25ns、2.25ns.…，为了确定时延Tg，我们还需要一个相邻频点的相位，假设这个频率为f2=1.01GHz，那么我们可以得到不同的时延Tg下，f1和f2的S21的相位S211和S212。
 

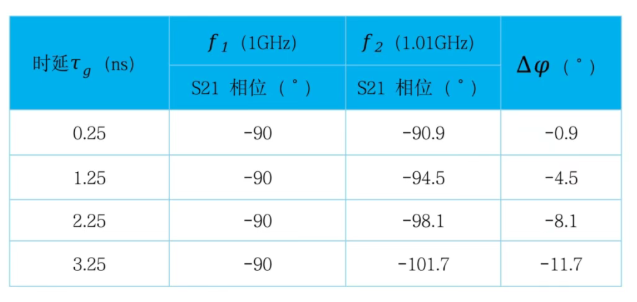
由此我们可以确定群时延Tg。

这两个频率的电磁波构成了一个“群”，我们实际计算的是这个“群”包络通过器件的时间，这也就是“群时延”这个名称的来源。当频率差趋近于无穷小时，差分变成了微分：
 

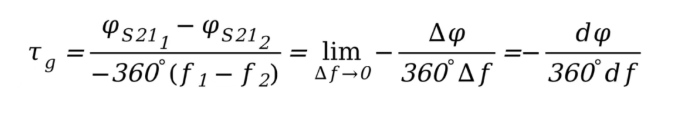
附录B：估算方法

工程上一般选择dp在45°以内。如果我们有被测件大致的群时延Tg值，△f最大值可以用以下方法来估算。
 

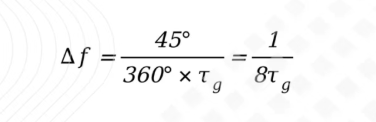
罗德与施瓦茨业务涵盖测试测量、技术系统、网络与网络安全，致力于打造一个更加安全、互联的世界。 成立 90 多年来，罗德与施瓦茨作为全球科技集团，通过发展尖端技术，不断突破技术界限。公司领先的产品和解决方案赋能众多行业客户，助其获得数字技术领导力。罗德与施瓦茨总部位于德国慕尼黑，作为一家私有企业，公司在全球范围内独立、长期、可持续地开展业务。