

对五种改善EMD端点效应的方法进行分析
描述
引言
1998 年,Huang 等人提出了一种新的信号处理方法:经验模态分解方法(Empirical Mode Decomposition,EMD)。它用不同特征尺度的数据序列本征模函数(Intrinsic Mode Function,IMF)分量来逐级分解信号。
该方法可以对一个非平稳信号进行平稳化处理。
在EMD分解中,每个IMF需要多次“筛选”过程,而每一次筛选过程,需要根据上、下包络计算出信号的局部平均值。上(下)包络是由信号的局部极大(小)值通过3次样条插值得到的。但信号的端点不可能同时处于极大值或极小值,因此上、下包络在数据序列两端会发散,且这种发散会随着运算的进行而逐渐向内,从而使得整个数据序列受到影响,这就是所谓的EMD 方法的端点效应。
国内外很多研究者对改进EMD端点效应问题进行了研究。目前,常用的EMD 端点效应处理方法有镜像法、极值延拓法、神经网络预测、多项式外延方法、平行延拓法、边界局部特征尺度延拓法。神经网络延拓算法的运算速度慢,在工程应用中实时性差。所以本文只对镜像法、极值延拓法、多项式法、平行延拓法和边界局部特征尺度延拓法进行比较,从而得到对工程应用有指导意义的结果。
1 EMD方法
EMD方法中假设:
(1)任何信号都可以分解为若干个IMF分量;
(2)各个IMF分量可以是线性的或非线性的,局部的零点数和极值点数相同,且上下包络关于时间轴局部对称;
(3)一个信号可包含若干个IMF分量。
每个IMF分量的计算步骤为:
首先,计算原信号x(t) 的极值点,然后用三次样条函数拟合出极大(小)值包络线e+(t)( e-(t))。原信号的均值包络m1(t) 是上下包络线的平均值:
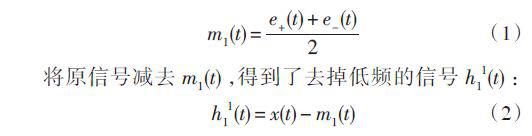
若h11(t) 不满足IMF 定义的条件,则它不是平稳信号,重复进行上述过程k 次( k 一般小于10),直到找到满足IMF的定义的h1k (t) ,则x(t) 的一阶IMF分量为:
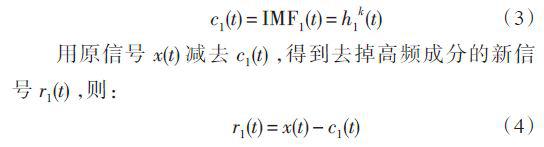
将r1(t) 作为原始数据,再得到第2个IMF分量c2 (t) ,依此类推,得到n 个IMF 分量,直到rn (t) 是单调函数或常量时,EMD分解过程停止。
最后,x(t) 经EMD分解后得到:
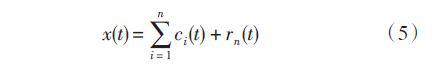
式中rn (t) 为趋势项,代表信号的平均趋势或均值。
2 改善端点效应的几种方法
本文在Matlab下实现了5种常用的改善EMD 端点效应的方法,并用于比较测试,它们分别为:
(1)端点镜像方法。以信号两端的边界为对称,把信号向外映射,得到原信号的镜像,形成一个闭合的曲线,从而得到完整的包络曲线。
(2)极值延拓法。以端点的一个特征波为依据,在两端各延拓两个极大值和极小值。
(3)多项式拟合法。对原信号的极值点序列,利用端点处3 个极值点进行多项式拟合计算出的值作为端点处极值点的近似取值,以确定边界极值点的位置。
(4)平行延拓法。利用端点附近的两个相邻极值点(一个极大值,一个极小值)处斜率相等这一特性,人为在两端定义出两个极值点。
(5)边界局部特征尺度延拓法。把调幅趋势和端点处局部极值点的时间间隔相结合,在信号两端分别添加一对极大值点和极小值点。
3 端点效应评价指标
本文采用3个指标来评价多种端点效应处理方法的效果:
(1)计算EMD 分解后各分量信号与对应的原信号之间的相似系数ρ 信号的包络发生形状畸变,引起端点效应,从而使各个分量的分解不准确。可以比较EMD分解后的各IMF分量和原信号分量之间的相似度,来评价各抑制端点效应算法的抑制效果。
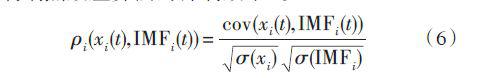
式中:cov-( ) 表示协方差;σ-( ) 表示方差;IMFi 表示信号经过EMD分解后的第i 个模态分量;xi 为相对应的原信号组成分量。ρ 值越大,说明端点效应的抑制越好。
(2)计算EMD 分解后得到的各IMF 分量和原信号相应的分量之间的平均相对误差[9].
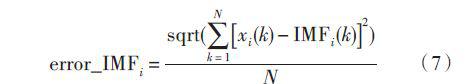
式中:N 表示信号的总个数;xi(k) 表示原信号第i 个分量;IMFi(k) 表示EMD 分解后得到的相应分量。
error_IMFi 越小,说明端点效应的抑制越好。
(3)运算时间。保证算法抑制端点效应效果的前提下,算法不能过于复杂,以满足实时性。
4 实验结果分析
假定测试信号是一个调频调幅非线性仿真信号,其表达式为:
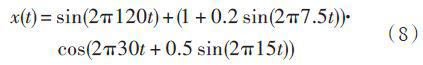
式中采样频率1 000 Hz,采样点数250 点,时域波形如图1所示。
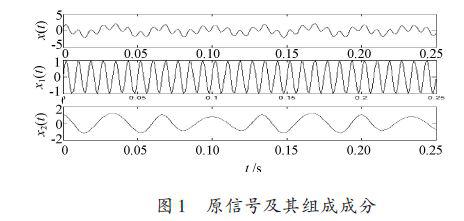
为了比较延拓后的分解结果,将原信号的组成分量一并给出,图2是没有进行端点处理的信号EMD分解结果,从图中可以看到,在两端点处有比较大的失真,并且会“ 向内污染”.图2~图7 中虚线为原分量;实线为EMD的分解结果。
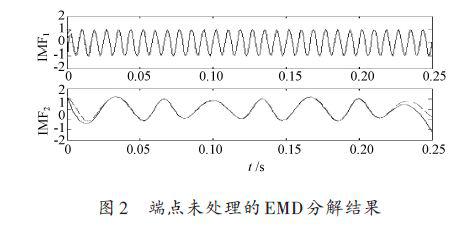
图3~图7分别是用端点镜像方法、多项式拟合法、极值延拓法、平行延拓法和边界局部特征尺度延拓法延拓后得到的EMD分解结果。
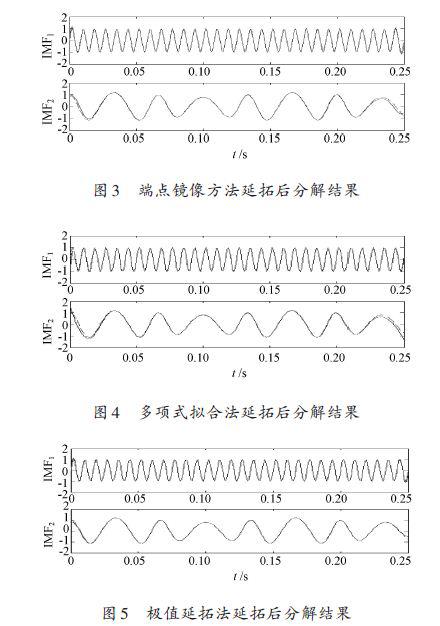
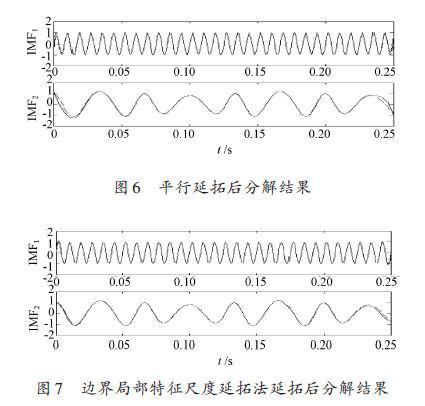
由图可知,这几种方法都有效改善了EMD 的端点效应,其中极值延拓法对于端点效应的改善比较明显,其他方法得到的结果,在两端仍有发散现象。表1给出了文中所述5种端点抑制方法对所给信号处理后的性能评价结果。
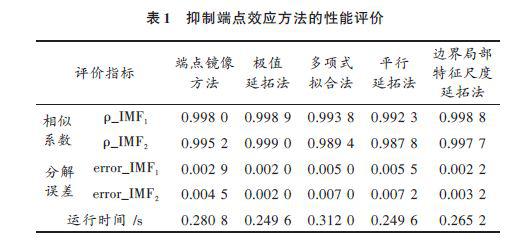
由表1给出参数可看出,对于给定准周期的测试信号,极值延拓法分解得到相似系数最大,分解误差最小,分解精度最高;平行延拓法得到的相似系数最小,分解误差最大,分解精度较低。比较运行时间,极值延拓法和平行延拓法计算速度最快,多项式拟合法耗时较长。
5 结语
在EMD 分解过程中,由于多次对局部极大值和局部极小值运用3次样条插值,从而产生了引起失真的端点效应。对于本文给出的准周期的测试信号,端点镜像方法、多项式拟合法、极值延拓法、平行延拓法和边界局部特征尺度延拓法5种方法都能改善EMD分解的端点效应问题。其中,极值延拓法是5种方法中分解效果最好的、运算速度最快的延拓方法,在工程技术应用中处理类似的信号,可以将其作为端点效应处理的主要方法。当然,工程应用中的信号千差万别,对于不同形式的信号,各种改善EMD 端点效应的延拓方法性能各异。在实际应用中,最好根据所处理信号的特点选择合适的延拓方法。本文所用评价方法,只对实际工程选用合适的延拓方法提供一个参考。
-
Python轴承故障诊断之经验模态分解EMD原理介绍2023-12-12 3619
-
基于EMD和自相关分析的轮胎音频信号处理2011-03-08 2456
-
emd算法实现2016-07-26 2734
-
请问能否在LabVIEW平台下编写改进后的EMD算法,采集到信号后直接进行分析?2019-10-09 2387
-
基于EMD的非平稳信号低通滤波技术的研究2009-09-03 720
-
空间矢量PWM逆变器死区效应分析与补偿方法2010-02-22 792
-
一种改进的语音端点检测方法研究2012-03-20 1145
-
基于EMD的语音功率谱分析2012-03-22 1194
-
改进EEMD电能质量检测方法(EMD分解信号)2017-10-28 1801
-
基于SSA的EMD去噪方法2017-11-21 4582
-
基于语音增强方法的语音端点检测2017-11-23 982
-
自适应局部均值的EMD方法2018-03-29 988
-
EMD信号处理方法如何在LabVIEW和MATLAB中的实现2019-10-17 2331
-
使用大数据进行社交网络中的从众效应和权威效应影响分析2019-10-30 1345
-
闲谈五种常用的数据分析方法2021-01-03 3388
全部0条评论

快来发表一下你的评论吧 !

