时序违例的修正与时序优化的思考方向

时序逻辑电路示意图如下。前后两级寄存器之间有一个组合逻辑运算电路。

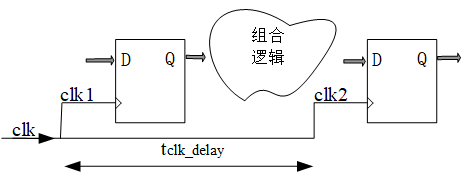
假设寄存器的建立时间要求为tsetup, 保持时间要求为thold, 输出延时为tcq（这些参数只要工艺库或者器件确定了，就是确定的）；组合逻辑电路的运算延时为tlogic; 两级寄存器之间的clk线路延时为tclk_delay；clk的随机抖动为tjitter；tcycle为时钟周期。故电路必须满足如下建立时间，保持时间要求：

tsetup_slack = tcycle-(tcq+tlogic) - tsetup+tclk_delay-tjitter>0

thold_slack = tcq+tlogic-thold-tclk_delay-tjitter>0

当tsetup_slack要求不满足时，我们可以选择增大tcycle。当然这就使得电路的整体时钟频率下降，从而速度下降。

从另一个角度考虑，我们可以通过减少tlogic来使得电路的建立时间裕量满足要求。  达到这个目的，只有两个办法：

第一是优化，简化组合逻辑电路，使得电路的延时下降。如果是ASIC设计，我们可以结合卡诺图，布尔逻辑等式代换，狄摩根定律等去对逻辑电路尽量做到优化。如果是FPGA设计，我们可以结合FPGA器件的底层单元（例如查找表（LUT））的基本逻辑功能去做逻辑优化。

例如，在做ASIC的时候，要实现如下逻辑功能：

输入	输出
A	C	D	B
0	0	0	0
0	0	1	1
0	1	0	0
0	1	1	1
1	0	0	0
1	0	1	1
1	1	0	1
1	1	1	0

 

经过卡诺图化简得到布尔表达式如下：

B=C’D+A’D+ACD’

还可以进一步化简

B=C’D+A’D+ACD’=(A’+C’)D+ACD’=(AC)’D+ACD’=(AC)^D

最后发现只要一个与门，后面跟一个异或门就可以实现这个逻辑。

（1）所以我们在写verilog的时候如果用门级电路去描述这个逻辑电路时：

assign B = (A&D)^D;

或者用结构化的方式去描述时：

and(AC,A,C);

xor(B,AC,D);

其综合对应出来的电路便可能是最简单的，当然这跟综合库有关。

（2）但是如果我们用行为级的方式去描述这个逻辑时，例如如下。

always @( * )

if( {A,C,D} == 3b001 ||  {A,C,D} == 3b011 || {A,C,D}==101 ||  {A,C,D} == 3b110)

B = 1b1;

else

B = 0;

那么其综合得到的电路就是不可控的了，虽然EDA工具会对其做优化。因此这样综合出来的电路如果不是最简的，那么其延时就大。

所以在描述电路的时候，如果时序要求很高，最好要考虑逻辑化简和器件适应。

第二种方式便是利用流水线技术，使得两级寄存器之间组合逻辑电路的运算量减少，从而使得tlogic减少。

例如对于一个组合逻辑电路，其功能是实现8bit数的全加器。我们可以将其划分成两个4bit数的全加器。如下图，原本是要实现两个8bit数A[7:0],B[7:0]，外加一个进位位c_in相加的，如下。

assign  {c_out,sum[7:0]} = A[7:0] + B[7:0] +c_in ;

现在变成了前面一个全加器实现

assign {c_out1,sum1[3:0]} = A[3:0] + B[3:0] + c_in ;

后面一个全加器实现

assign {c_out,sum2[3:0]} = A[7:4] + B[7:4] + c_out1 ;

最后再将sum1，sum2合并得到sum，如下。

assign  sum = {sum2,sum1};

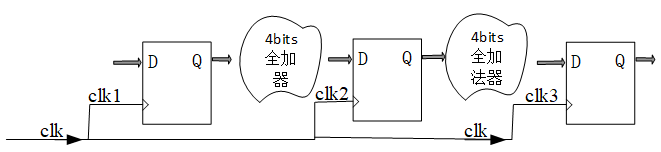
第一个全加器算出 {c_out1,sum1[3:0]} = A[3:0] + B[3:0] + c_in  之后，在时钟有效沿到来时，将c_out1,sum1[3:0],A[7:4],B[7:4] 送到中间一级寄存器暂存；然后第二个电路做  {c_out,sum2[3:0]} = A[7:4] + B[7:4] + c_out1 运算，并将结果sum1，sum2合并得到sum。这样一来每两级寄存器之间的全加器变成了4bit的全加器，电路延时肯定得到降低了。从而tlogic降低。

当然还可以进一步优化，使得流水级数更多。一般来说保持时间不会出现违例情况，因为寄存器的输出延时tcq,一般要大于thold。如果出现违例，从式子 

thold_slack = tcq+tlogic-thold-tclk_delay-tjitter>0

我们可以考虑适当增加tlogic，或者后端布局布线时去减少tclk_delay。