深度学习背后的线性代数问题

深度学习从入门到放弃？一定是哪里出了问题。

这篇文章想来和你探讨下：深度学习背后的线性代数问题。

先做个简单的名词解释

深度学习：作为机器学习的一个子域，关注用于模仿大脑功能和结构的算法：人工神经网络。

线性代数：连续的而不是离散的数学形式，许多计算机科学家不太了解它。对于理解和使

用许多机器学习算法，特别是深度学习算法，理解线性代数是非常重要的。

为什么需要数学？

线性代数，概率和微积分是机器学习用于表述的「语言」。学习这些主题将有助于深入理解底层算法机制，便于开发新算法。

当限定在更小的层次时，深度学习背后的基础都是数学。所以在开始深度学习和编程之前，理解基本的线性代数是至关重要的。

深度学习背后的核心数据结构是标量，向量，矩阵和张量。让我们以编程方式用这些解决所有基本的线性代数问题。

标量

标量是单个数字，是一个 0 阶张量的例子。符号 x∈ℝ 表示 x 是一个标量，属于一组实数值 ℝ。

深度学习有不同的有趣的数字集合。ℕ 表示正整数集合（1,2,3，...）。ℤ 表示实数，包括正值，负值和 0。ℚ 表示有理数的集合，有理数可以表示为两个整数组成的分数。

Python 中内置一些标量类型 int，float，complex，bytes 和 Unicode。在 NumPy 这个 python 库中，有 24 种新的基本数据类型来描述不同类型的标量。有关数据类型的信息，请参阅此处的文档

（https://docs.scipy.org/doc/numpy-1.14.0/reference/arrays.scalars.html）

在 Python 中定义标量和一些操作：

下面的代码片段解释了对标量的几个算术运算。

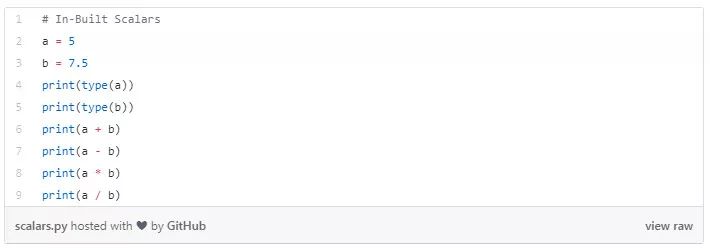
以下代码片段检查给定变量是否是标量。

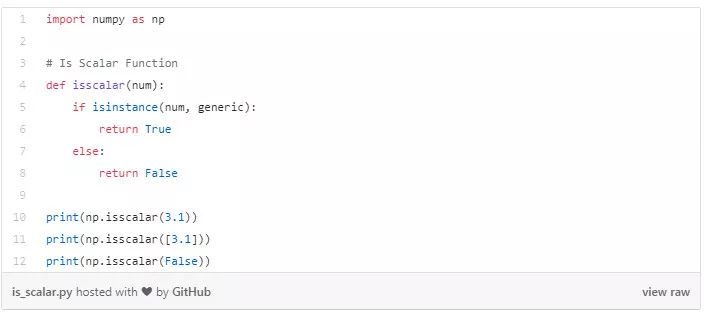
向量

向量是一维有序数组，是一阶张量的例子。向量被称为向量空间的对象的片段。向量空间可以被认为是特定长度（或维度）的所有可能向量的全部集合。三维实值向量空间（用 ℝ^3 表示）通常用于从数学角度表示我们对三维空间的现实世界概念。

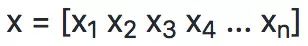
为了明确识别向量的必要成分，向量的第 i 个标量元素被写为 x [i]。

在深度学习中，向量通常表示特征向量，其原始组成部分定义特定特征的相关性。这些元素中可能包括二维图像中像素集强度的相关重要性或者金融工具的横截面的历史价格值。

Python 中定义向量和一些操作：

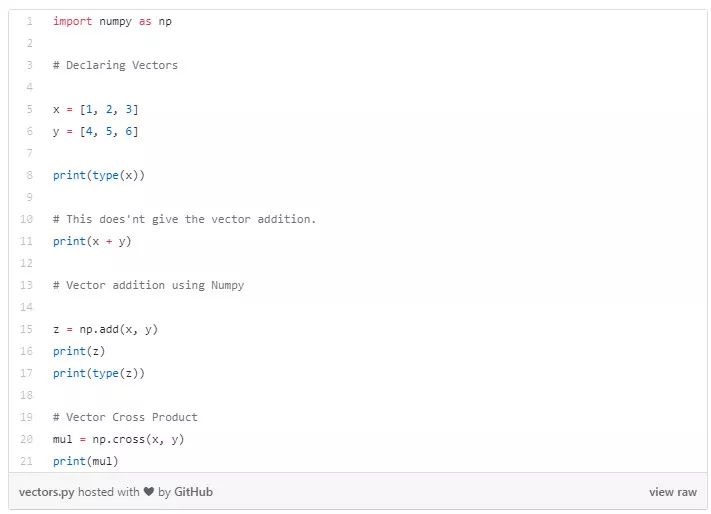
矩阵

矩阵是由数字组成的矩形阵列，是二阶张量的一个例子。如果 m 和 n 均为正整数，即 m, n ∈ ℕ，则矩阵包含 m 行 n 列，共 m*n 个数字。

完整的矩阵可写为：

将所有矩阵的元素缩写为以下形式通常很有用。

在 Python 语言中，我们使用 numpy 库来帮助我们创建 n 维数组。这些数组基本上都是矩阵，我们使用矩阵方法通过列表，来定义一个矩阵。

$python

在 Python 中定义矩阵的操作：

矩阵加法

矩阵可以与标量、向量和其他的矩阵相加。这些运算都有严格的定义。这些技巧在机器学习和深度学习中会经常用到，所以值得熟练运用这些技巧。

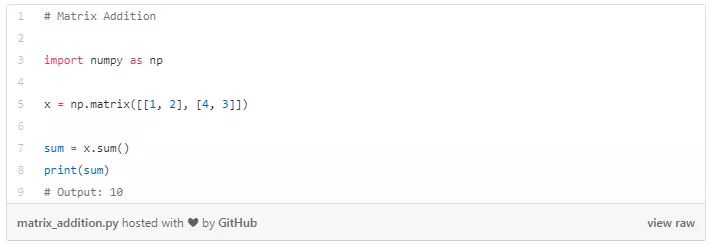
矩阵-矩阵加法

C=A+B（矩阵 A 和 B 应该有相同的形状）

这类方法返回矩阵的形状，并将两个参数相加后返回这些矩阵的总和。如果这些矩阵的形状不相同，则程序会报错，无法相加。

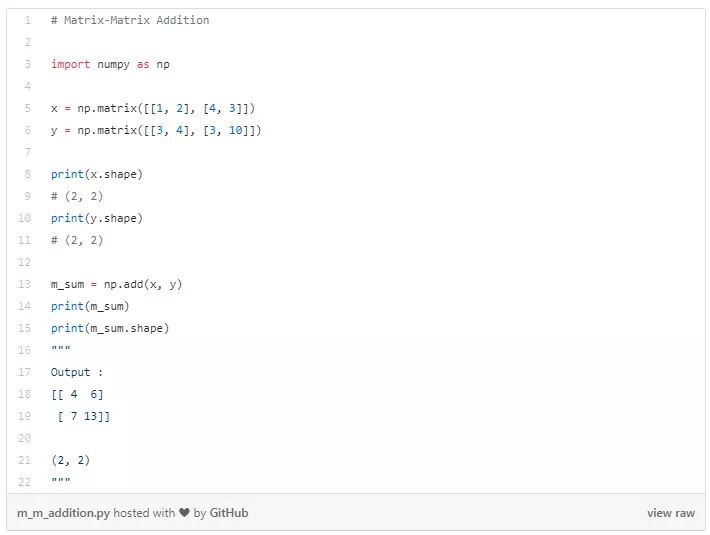
矩阵-标量相加

将给定的标量加到给定矩阵的所有元素。

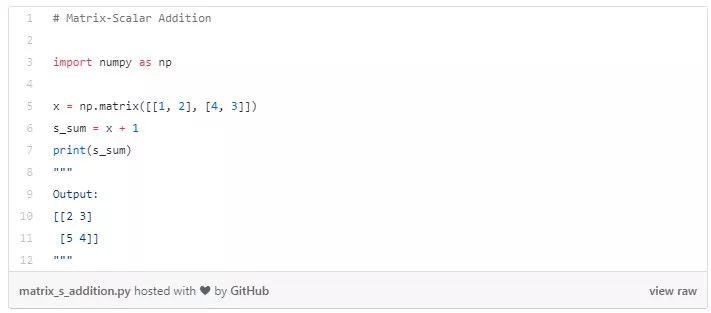
矩阵-标量相乘

用给定的标量乘以给定矩阵的所有元素。

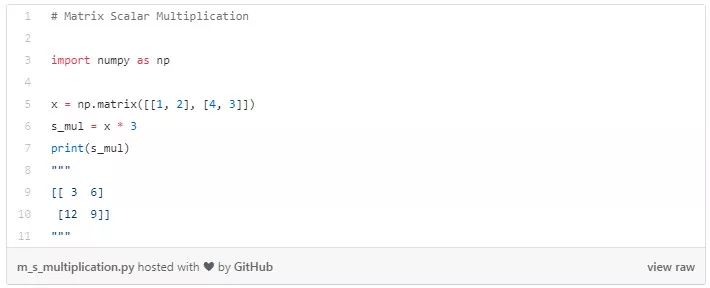
矩阵乘法

矩阵 A 与矩阵 B 相乘得到矩阵 C。

矩阵转置

通过矩阵转置，你可以将行向量转换为列向量，反之亦然。

A=[aij]mxn

AT=[aji]n×m

张量

张量的更一般的实体封装了标量、向量和矩阵。在物理学科和机器学习中有时需要用到高于二阶的张量。

我们使用像 tensorflow 或 Pytorch 这样的 Python 库来声明张量，而不是用嵌套矩阵。

在 Pytorch 中定义一个简单的张量:

Python 中张量的几点算术运算