关于LSTM和GRU的详细图解指南

机器学习工程师 Michael Nguyen 在其博文中发布了关于 LSTM 和 GRU 的详细图解指南。博文中，他先介绍了 LSTM 和 GRU 的本质， 然后解释了让 LSTM 和 GRU 有良好表现的内部机制。 当然，如果你还想了解这两种网络背后发生了什么，那么这篇文章就是为你准备的。

▌短时记忆

RNN 会受到短时记忆的影响。如果一条序列足够长，那它们将很难将信息从较早的时间步传送到后面的时间步。 因此，如果你正在尝试处理一段文本进行预测，RNN 可能从一开始就会遗漏重要信息。

在反向传播期间，RNN 会面临梯度消失的问题。 梯度是用于更新神经网络的权重值，消失的梯度问题是当梯度随着时间的推移传播时梯度下降，如果梯度值变得非常小，就不会继续学习。

梯度更新规则

因此，在递归神经网络中，获得小梯度更新的层会停止学习—— 那些通常是较早的层。 由于这些层不学习，RNN 可以忘记它在较长序列中看到的内容，因此具有短时记忆。

▌作为解决方案的 LSTM 和 GRU

LSTM 和 GRU 是解决短时记忆问题的解决方案，它们具有称为“门”的内部机制，可以调节信息流。

这些“门”可以知道序列中哪些重要的数据是需要保留，而哪些是要删除的。 随后，它可以沿着长链序列传递相关信息以进行预测，几乎所有基于递归神经网络的技术成果都是通过这两个网络实现的。

LSTM 和 GRU 可以在语音识别、语音合成和文本生成中找到，你甚至可以用它们为视频生成字幕。对 LSTM 和 GRU 擅长处理长序列的原因，到这篇文章结束时你应该会有充分了解。 

下面我将通过直观解释和插图进行阐述，并避免尽可能多的数学运算。

本质

让我们从一个有趣的小实验开始吧。当你想在网上购买生活用品时，一般都会查看一下此前已购买该商品用户的评价。

当你浏览评论时，你的大脑下意识地只会记住重要的关键词，比如“amazing”和“awsome”这样的词汇，而不太会关心“this”、“give”、“all”、“should”等字样。如果朋友第二天问你用户评价都说了什么，那你可能不会一字不漏地记住它，而是会说出但大脑里记得的主要观点，比如“下次肯定还会来买”，那其他一些无关紧要的内容自然会从记忆中逐渐消失。

而这基本上就像是 LSTM 或 GRU 所做的那样，它们可以学习只保留相关信息来进行预测，并忘记不相关的数据。

▌RNN 述评

为了了解 LSTM 或 GRU 如何实现这一点，让我们回顾一下递归神经网络。 RNN 的工作原理如下；第一个词被转换成了机器可读的向量，然后 RNN 逐个处理向量序列。

逐一处理矢量序列

处理时，RNN 将先前隐藏状态传递给序列的下一步。 而隐藏状态充当了神经网络记忆，它包含相关网络之前所见过的数据的信息。

将隐藏状态传递给下一个时间步

让我们看看 RNN 的一个细胞，了解一下它如何计算隐藏状态。 首先，将输入和先前隐藏状态组合成向量， 该向量包含当前输入和先前输入的信息。 向量经过激活函数 tanh之后，输出的是新的隐藏状态或网络记忆。

RNN 细胞

激活函数 Tanh

激活函数 Tanh 用于帮助调节流经网络的值。 tanh 函数将数值始终限制在 -1 和 1 之间。

当向量流经神经网络时，由于有各种数学运算的缘故，它经历了许多变换。 因此想象让一个值继续乘以 3，你可以想到一些值是如何变成天文数字的，这让其他值看起来微不足道。

没有 tanh 函数的向量转换

tanh 函数确保值保持在 -1~1 之间，从而调节了神经网络的输出。 你可以看到上面的相同值是如何保持在 tanh 函数所允许的边界之间的。

有 tanh 函数的向量转换

这是一个 RNN。 它内部的操作很少，但在适当的情形下（如短序列）运作的很好。 RNN 使用的计算资源比它的演化变体 LSTM 和 GRU 要少得多。

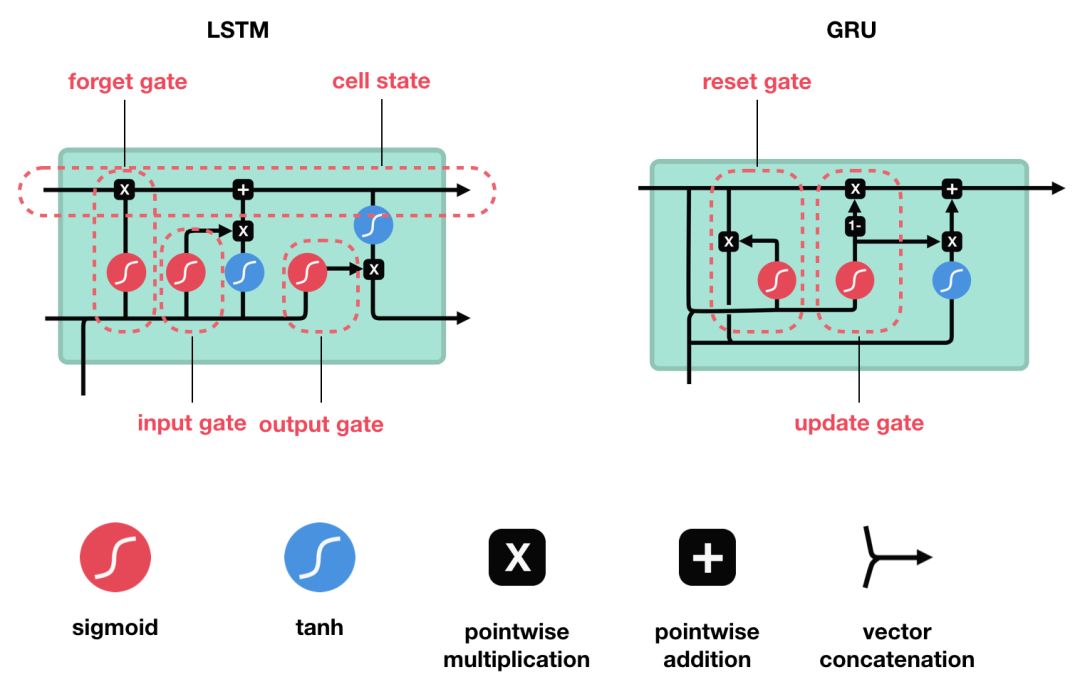
▌LSTM

LSTM 的控制流程与 RNN 相似，它们都是在前向传播的过程中处理流经细胞的数据，不同之处在于 LSTM 中细胞的结构和运算有所变化。

LSTM 的细胞结构和运算

这一系列运算操作使得 LSTM具有能选择保存信息或遗忘信息的功能。咋一看这些运算操作时可能有点复杂，但没关系下面将带你一步步了解这些运算操作。

核心概念

LSTM 的核心概念在于细胞状态以及“门”结构。细胞状态相当于信息传输的路径，让信息能在序列连中传递下去。你可以将其看作网络的“记忆”。理论上讲，细胞状态能够将序列处理过程中的相关信息一直传递下去。

因此，即使是较早时间步长的信息也能携带到较后时间步长的细胞中来，这克服了短时记忆的影响。信息的添加和移除我们通过“门”结构来实现，“门”结构在训练过程中会去学习该保存或遗忘哪些信息。

Sigmoid

门结构中包含着 sigmoid 激活函数。Sigmoid 激活函数与 tanh 函数类似，不同之处在于 sigmoid 是把值压缩到 0~1 之间而不是 -1~1 之间。这样的设置有助于更新或忘记信息，因为任何数乘以 0 都得 0，这部分信息就会剔除掉。同样的，任何数乘以 1 都得到它本身，这部分信息就会完美地保存下来。这样网络就能了解哪些数据是需要遗忘，哪些数据是需要保存。

Sigmoid 将值压缩到 0~1 之间

接下来了解一下门结构的功能。LSTM 有三种类型的门结构：遗忘门、输入门和输出门。

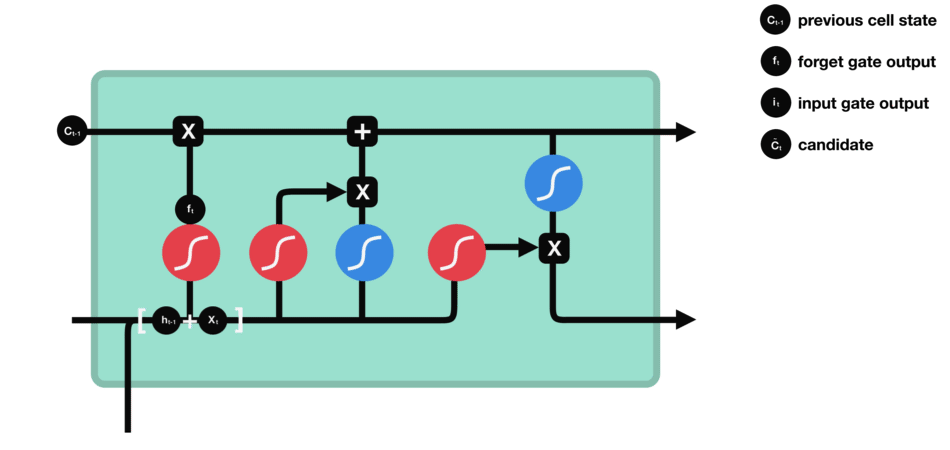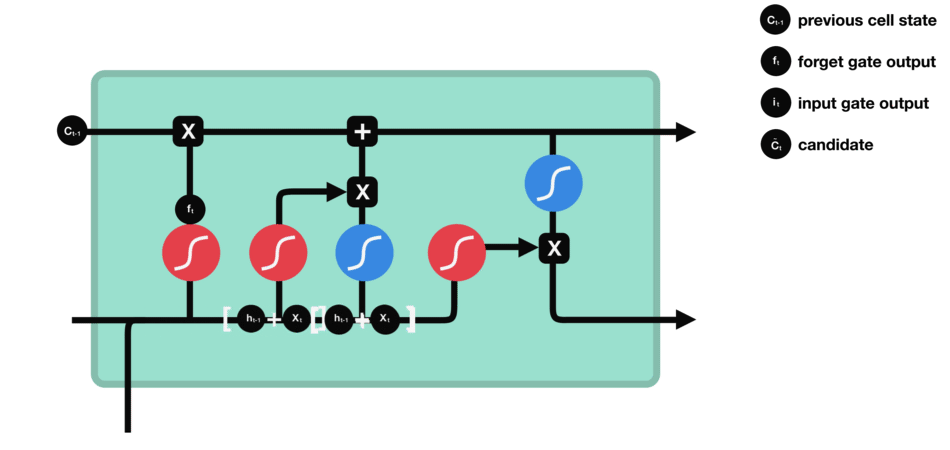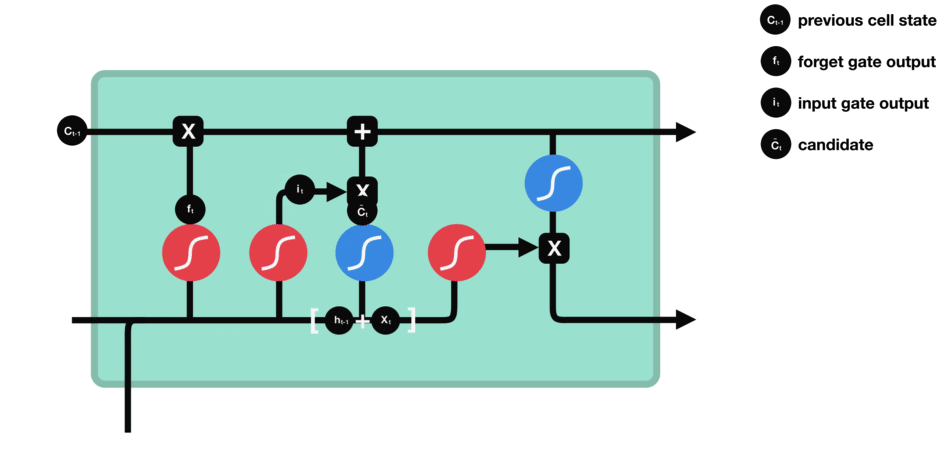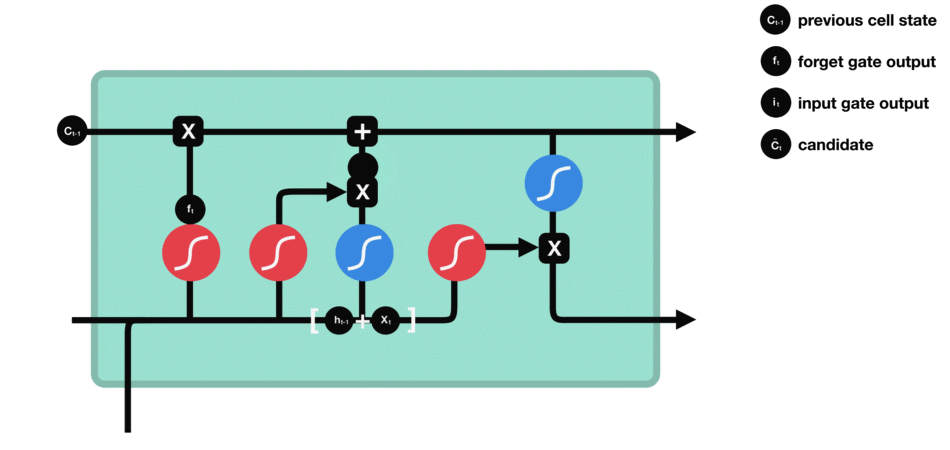
遗忘门

遗忘门的功能是决定应丢弃或保留哪些信息。来自前一个隐藏状态的信息和当前输入的信息同时传递到 sigmoid 函数中去，输出值介于 0 和 1 之间，越接近 0 意味着越应该丢弃，越接近 1 意味着越应该保留。

遗忘门的运算过程

输入门

输入门用于更新细胞状态。首先将前一层隐藏状态的信息和当前输入的信息传递到 sigmoid 函数中去。将值调整到 0~1 之间来决定要更新哪些信息。0 表示不重要，1 表示重要。

其次还要将前一层隐藏状态的信息和当前输入的信息传递到 tanh 函数中去，创造一个新的侯选值向量。最后将 sigmoid 的输出值与 tanh 的输出值相乘，sigmoid 的输出值将决定 tanh 的输出值中哪些信息是重要且需要保留下来的。

输入门的运算过程

细胞状态

下一步，就是计算细胞状态。首先前一层的细胞状态与遗忘向量逐点相乘。如果它乘以接近 0 的值，意味着在新的细胞状态中，这些信息是需要丢弃掉的。然后再将该值与输入门的输出值逐点相加，将神经网络发现的新信息更新到细胞状态中去。至此，就得到了更新后的细胞状态。

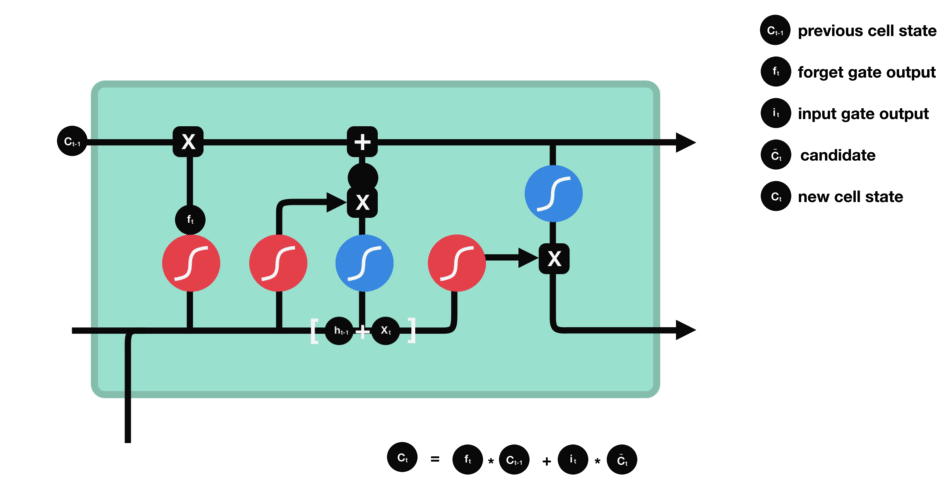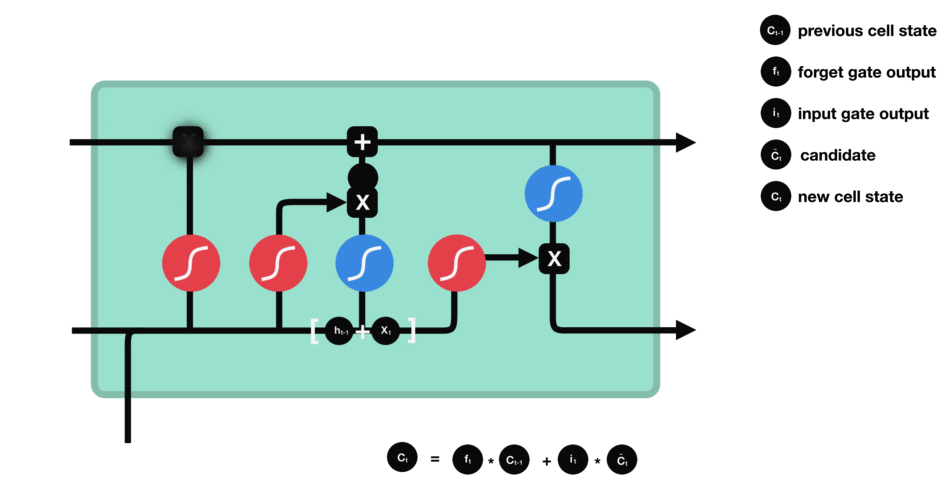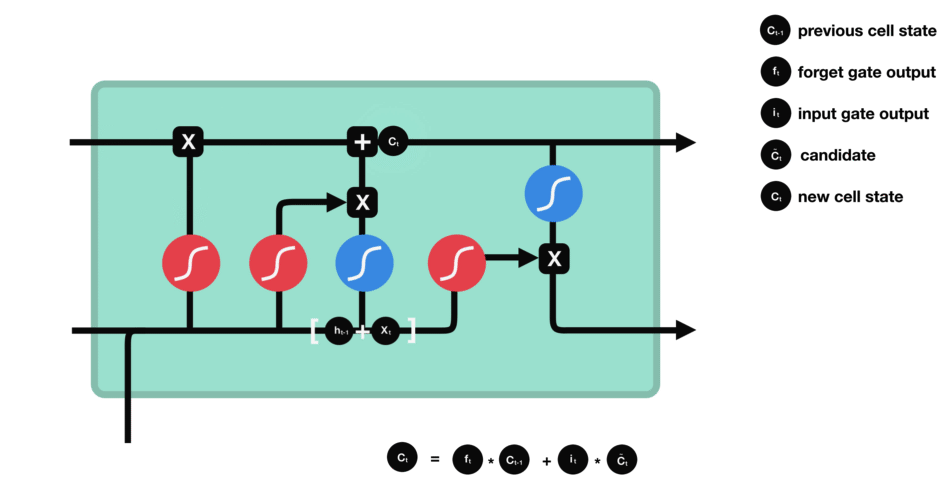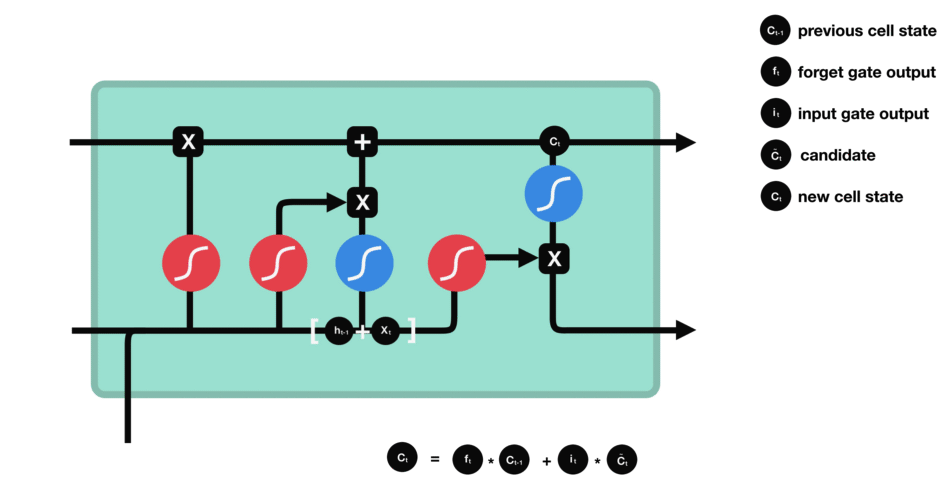
细胞状态的计算

输出门

输出门用来确定下一个隐藏状态的值，隐藏状态包含了先前输入的信息。首先，我们将前一个隐藏状态和当前输入传递到 sigmoid 函数中，然后将新得到的细胞状态传递给 tanh 函数。

最后将 tanh 的输出与 sigmoid 的输出相乘，以确定隐藏状态应携带的信息。再将隐藏状态作为当前细胞的输出，把新的细胞状态和新的隐藏状态传递到下一个时间步长中去。

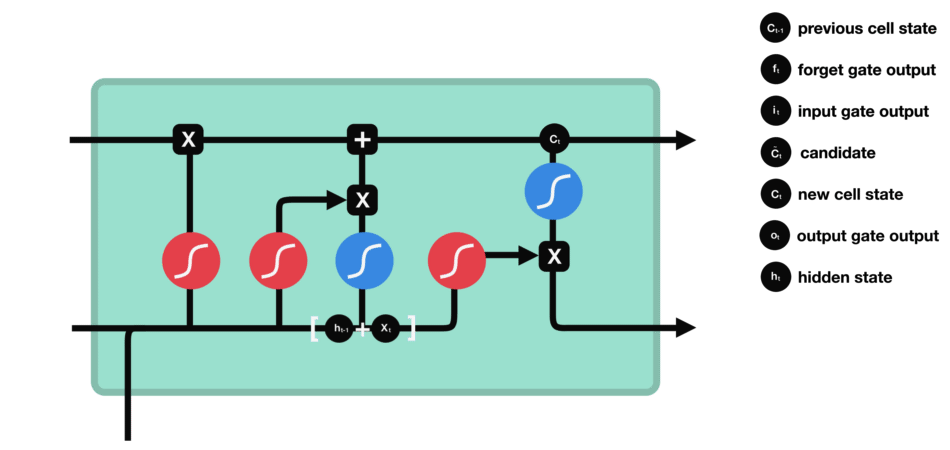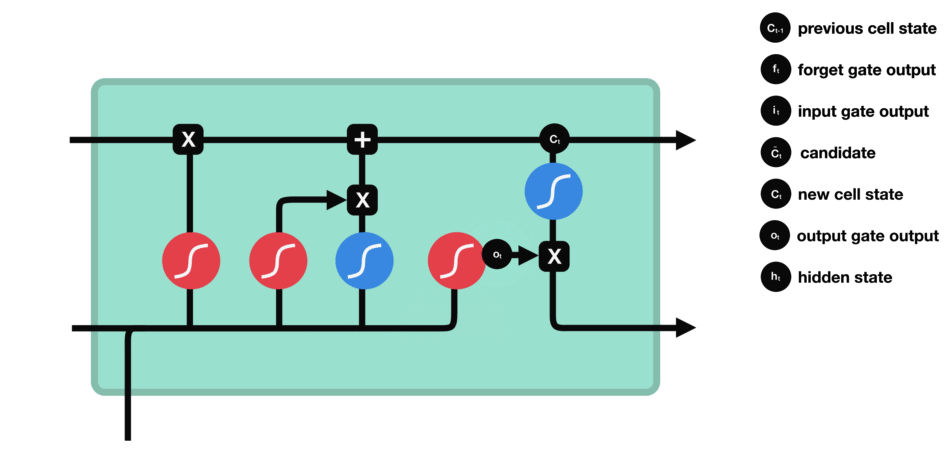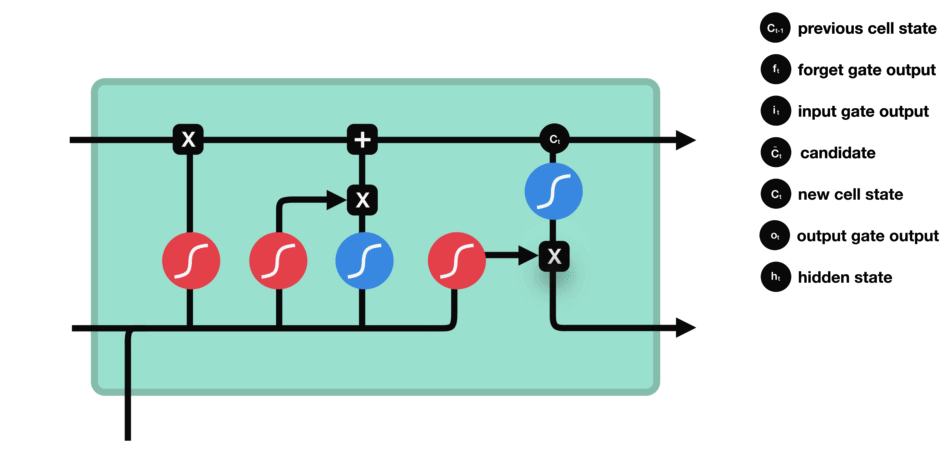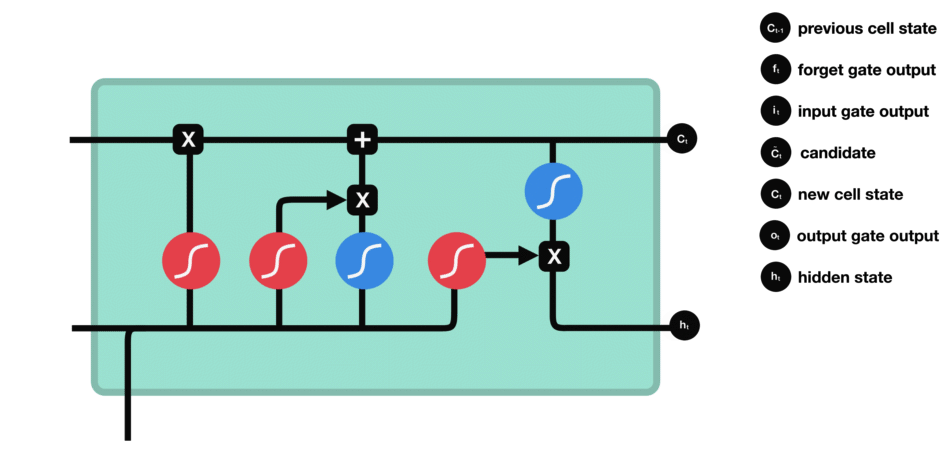
 输出门的运算过程

让我们再梳理一下。遗忘门确定前一个步长中哪些相关的信息需要被保留；输入门确定当前输入中哪些信息是重要的，需要被添加的；输出门确定下一个隐藏状态应该是什么。

代码示例

对于那些懒得看文字的人来说，代码也许更好理解，下面给出一个用 python 写的示例。

python 写的伪代码

1.首先，我们将先前的隐藏状态和当前的输入连接起来，这里将它称为 combine；

2.其次将 combine 丢到遗忘层中，用于删除不相关的数据；

3.再用 combine 创建一个候选层，候选层中包含着可能要添加到细胞状态中的值；

4.combine 同样要丢到输入层中，该层决定了候选层中哪些数据需要添加到新的细胞状态中；

5.接下来细胞状态再根据遗忘层、候选层、输入层以及先前细胞状态的向量来计算；

6.再计算当前细胞的输出；

7.最后将输出与新的细胞状态逐点相乘以得到新的隐藏状态。

是的，LSTM 网络的控制流程就是几个张量和一个 for 循环。你还可以使用隐藏状态进行预测。结合这些机制，LSTM 能够在序列处理中确定哪些信息需要记忆，哪些信息需要遗忘。

▌GRU

知道了 LSTM 的工作原理之后，来了解一下 GRU。GRU 是新一代的循环神经网络，与 LSTM 非常相似。与 LSTM 相比，GRU 去除掉了细胞状态，使用隐藏状态来进行信息的传递。它只包含两个门：更新门和重置门。

GRU 的细胞结构和门结构

更新门

更新门的作用类似于 LSTM 中的遗忘门和输入门。它决定了要忘记哪些信息以及哪些新信息需要被添加。

重置门

重置门用于决定遗忘先前信息的程度。

这就是 GRU。GRU 的张量运算较少，因此它比 LSTM 的训练更快一下。很难去判定这两者到底谁更好，研究人员通常会两者都试一下，然后选择最合适的。

▌结语

总而言之，RNN 适用于处理序列数据用于预测，但却受到短时记忆的制约。LSTM 和 GRU 采用门结构来克服短时记忆的影响。门结构可以调节流经序列链的信息流。LSTM 和 GRU 被广泛地应用到语音识别、语音合成和自然语言处理等。