基于隐马尔可夫模型( HMM )开发了一个驾驶行为预测模型

摘要-先进的驾驶员辅助系统( ADAS )的开发在预测驾驶行为的研究中起着重要作用。我们开发了一种基于隐马尔可夫模型( HMM )的预测人类驾驶行为的方法。包括左/右车道变换和车道保持在内的三种不同的驾驶动作被建模为HMM的隐藏状态。基于观察(训练)，HMM方法能够使用观察到的序列来计算最可能的驾驶行为。此外，在建模过程中，观察到的序列也用于HMM的训练。为了提高模型的预测性能，我们提出了一种预滤波器将采集的信号量化为具有特定特征的观测序列。

在本论文中，将讨论并最终优化合适预过滤器的定义。这里最优性被定义为将车辆环境映射到量化状态的预滤波器的最优段。结合基于HMM的精度、检测和虚警率方面的相关结果，可以确定预滤波器的最佳参数集。利用真实人类驾驶行为的实验数据(取自驾驶模拟器)，可以得出结论，预过滤器的最佳定义可以提高检测率和准确性，同时降低误报率。驾驶行为预测的有效性已经通过与其他方法的比较得到了成功的证明

I介绍

驾驶员辅助系统是为了帮助人类驾驶员更好、更安全驾驶而开发的系统。典型的辅助驾驶系统侧重于探测危险场景并发出警告从而避免交通事故。这类辅助系统的预测是基于诸如距离和车速等物理变量来计算的。这些物理变量描述了车辆状态和行驶环境。虽然车辆状态和驾驶环境与当前的驾驶安全评估相关，但最常见的事故原因与人类行为有关。因此，辅助驾驶系统应该帮助驾驶员检测可能的不当行为。然而，遵循一般驾驶规则，司机通常会根据自己的驾驶经验和习惯选择最合适的操作。司机的驾驶行为被认为是个人的。因此，驾驶辅助系统应该基于对个体驾驶行为的分析进行调整，以提高交通安全并实现智能驾驶。个人驾驶行为受许多因素影响，包括当前环境条件、个人驾驶特征等。因此，驾驶员的意图和下一次驾驶动作不能通过物理变量来简单而直接地测量。

为了建立驾驶行为模型，一些方法已经被提出。例如，神经网络( NN )模型已经被用于预测[ 1 ]高速公路上车辆跟驰的加速度分布。在[ 2 ]动态贝叶斯网络( DBN )被用于估计和预测四向交叉路口的车辆跟踪和变道的加速度以及转弯率。在[ 3 ]中，通过使用特征函数来评估情境情境，预测交通参与者的下一个状态，提出了一个完全概率模型。《[ 4 ]》的作者使用了一个模糊逻辑( FL )模型，该模型是由驾驶员根据经验观察到的高速信号交叉口的行为建立的。

在我们的研究中，使用了隐马尔科夫模型( HMM )方法预测驾驶行为，该方法用于估计不可观察状态，不可观测状态可以通过基于期望最大化( EM )和最大似然估计( MLE )的观测状态来推断，这是分别估计HMM参数和最可能隐藏状态的标准方法[ 5 ] [ 6 ]。为了改进性能建模，必须定义观察状态的适当部分。实验结果显示，使用那些合适的观察段范围，可以提高驾驶行为预测模型的质量。

Ⅱ基于隐马尔可夫模型的驾驶行为预测

隐马尔可夫模型（HMM）已经被成功应用于语音识别和合成[7]、生物学中的DNA轮廓识别[8]以及视频[9]中的人类行为识别等领域。如今，HMM的应用已经扩展到越来越多的研究领域，例如驾驶行为识别和预测。在[10]中，作者提出使用HMM来确定各种车辆操纵的驾驶员意图。此外，HMM通常与其他算法一起使用。在[11]中，作者提出了一种混合状态系统（HSS）-HMM框架，用于估计交叉口的驾驶员行为。驾驶员行为和车辆动力学被建模为HSS， HSS提供系统架构，HMM定义系统组件之间的关系，HMM和相关基本算法的详细定义在[5]中描述。

HMM描述了两个随机过程之间的关系：一个由一组未观察到的(隐藏的)状态S = {S1，S2，...SN}，其中N为无法直接测量的隐藏状态的数量。另一个随机过程由一组M个可观察符号V ={V1，V2，...VM}。隐藏状态和观察符号位于，时间t分别被定义为Qt和Ot。因此，隐藏状态序列是Q= {Q1，Q2，...QT}，观察序列是O = {O1，O2，...OT}，其中T是序列的长度。使用HMM参数的序列可以通过分析观察序列来确定未观察到的状态。

在我们的研究中，驾驶行为主要考虑车道变换。执行的驾驶操纵是隐藏状态。它们包括左/右车道变换和正常车道保持，因此N = 3.驾驶行为预测模型可视为标准HMM，如图1所示

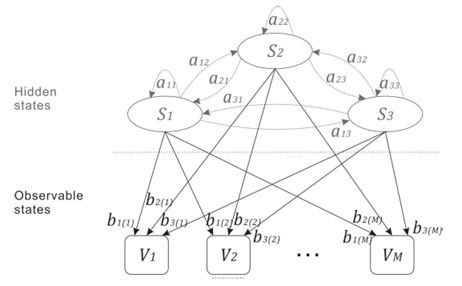
图1.具有3种状态的HMM模型

驱动行为表示为Si，观察值Vk表示为下标k。该模型可以定义为一种系统，其中驾驶行为以状态转移概率ai j = P（Qt = S j | Qt-1 = Si），i，j [1，N]切换到另一个，这意味着从状态Si移动到状态S j的概率。所有转移概率ai j可以构成状态转移概率矩阵

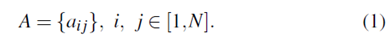
观察概率b j ( k )定义了在时间t从状态S j产生观察Vk的概率，这意味着b j ( k ) = P ( Ot = Vk | Qt = S j )。相应的观测概率分布矩阵表示为

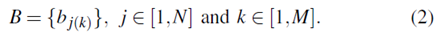
为了描述HMM，有必要使用初始概率分布，其指示在状态Si中开始的概率，其中

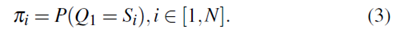
使用以上定义，完整的HMM可以定义为λ= ( A，B，π)。

为了实现基于HMM的驾驶行为预测，该过程必须分为两部分：第一部分是模型的训练，第二部分是估计最可能的隐藏状态序列。为了训练HMM，Baum - Welch算法（也称为期望最大化）将被用来估计最大似然模型参数λ= ( A，B，π)。在给定的观察序列O及其对应的隐藏状态序列Q中，HMM λ的参数被计算和调整以最佳地拟合这两个序列。基于保存的HMM λ，使用Viterbi算法计算具有最高概率的驾驶行为的最可能序列。

如前所述，隐藏状态序列将由观察序列确定。因此，选择描述组成观察状态的当前状况的参数是非常重要的。这些参数必须考虑到数据收集的可行性，并具备达到模型识别目的的能力。当司机在高速公路上行驶时，ego车辆和其他周围车辆之间的关系是影响司机决策的主要因素。在我们的研究者中，与前方车辆的相对速度、ego车辆和周围车辆之间的距离被选择作为观察变量，即时间t的观察向量被定义为

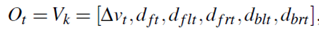
其中k∈[ 1，M ]，M是观察选择的数量。表I给出了参数的细节。在我们的研究中，驾驶模拟器用于收集每个参数的数据。在现实世界中，这些参数将取自不同的传感器，如照相机、雷达、激光雷达和超声波。[12]

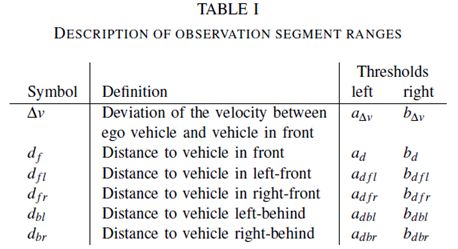
在驾驶过程中，所有观察参数都被认为是可测量的。信号是动态的，随时间变化。每个参数的改变将导致观察向量的改变。这里假设通过预滤波实现的量化信号，这在汽车领域中是典型的，使用精度有限的相关电子设备。在预滤波器的输出端，导出了以特征向量为特征的量化信号。通过使用特征向量，应该区分不同的驾驶情况。基于预滤波器，每个观测参数的信号数据将被分成多个段。每个片段代表一个相应的观察结果。因此，线段的范围很重要，将被定义来描述观察结果。使用这些分段范围，可以处理和组合信号以形成HMM预测过程的特征。为了简化建模过程，在这个贡献中定义了一个预滤波器，它只使用两个不同的范围值，并将每个观测参数分成三个部分。表I中显示了每个观测参数的左阈值和右阈值(即两个范围值)。显然，观测段范围的值非常重要，因为它们隐含地定义了HMM训练的观测序列，并最终影响了精度。

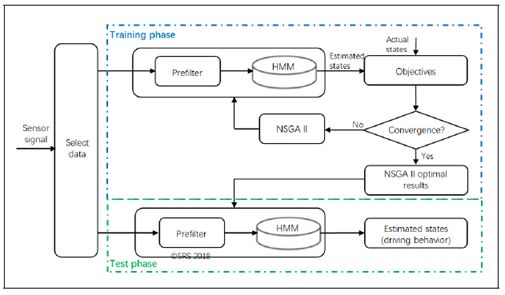
图2.最佳预过滤器定义说明

一个简单的方法是根据一般驾驶规则选择一个通用预过滤器，例如在德国，50m是高速公路上两个导向柱之间的相应距离。因此，距离的分段范围值可以定义为50m和100 m，速度计上的间隔可以用来表示相对速度的范围值，例如10公里/小时和20公里/小时。

预测过程的核心是通过HMM来实现的。使用给定的隐藏状态序列及其相应的观察序列，可以训练HMM。因此，输入到HMM的特征向量可以通过使用通用预滤波器来提取，这有助于确定最佳HMM并提高预测性能。出于这个原因，对于每个驱动器，可以生成具有个性化最佳预滤波器的HMM。

在图2中，示出了产生最佳预过滤器的过程。为了定义最佳预过滤参数，使用非支配排序遗传算法II ( NSGA - II )。NSGA - II源自NSGA，用于解决多目标优化问题( MOPs ) [ 16 ]。通过使用NSGA - II，使用不同的范围值重复训练HMM。考虑所有可能的范围值，每个范围从该参数的最小值变为最大值。确定每个观测参数的最佳阈值(最佳预滤波器)以最小化目标函数。

准确度( ACC )、检测率( DR )和虚警率( FAR )被广泛用于评估分类器[ 13 ] [ 14 ]。

它们是基于真阳性( TP )、假阳性( FP )、真阴性( TN )以及假阴性( FN )数来计算的。为了解释，举例说明了一个混淆矩阵(图3 )来描述向右改变车道的参数。真阳性( TP )表示

图3.混淆矩阵的说明[车道改为右]

它们的计算基于真阳性（TP），误报（FP），真阴性（TN）以及假阴性（FN）数。为了解释，示出了混淆矩阵（图3）作为示例来描述用于向右改变车道的参数。真阳性（TP）表示当估计的机动是正的时（向右改变车道）并且实际的也是正的事件的数量，对比度假阳性（FP）表示当估计的机动是正的时的事件的数量和实际值不相同，对于真假阴性（TN / FN）。 ACC，DR和FAR由[14]定义

如前所述，每个观察参数（预滤波器）的左/右阈值是确定HMM训练的观察序列的临界值，因此影响估计的状态。 TP，FP，TN和FN的值将由估计的状态定义，并最终影响ACC，DR和FAR值。在研究中，将针对前述ACC，DR和FAR参数的改进来选择最佳预滤波器。因此，目标函数定义为

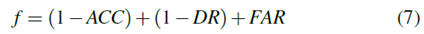
三种驾驶行为。

III.实验结果

本节介绍了基于HMM的变道机动预测的实验装置和获得的结果。使用所提出的模型，基于测量的变化和速度，预测了驾驶员的车道变换行为。为了提高预测性能，必须定义最佳预滤波器(特征参数)。

A.实验设计

应用如图4所示的专业驾驶模拟器SCANeRTMstudio来收集驾驶数据，该驾驶数据用于训练和测试所提出的方法。该模拟器配备五个监视器，180度视野，基座固定驾驶员座椅，方向盘和踏板。三个后视镜是决定改变车道所必需的，它们显示在显示器的相应位置上，驾驶模拟器的数据获取频率为20Hz。

图4.驾驶模拟器，椅子动力学和控制，U DuE

驾驶场景基于高速公路驾驶场景，具有四个车道的两个方向和模拟的交通环境。在驾驶期间，当前车缓慢行驶时，参与者可以执行超车操纵。超车后，参与者也可以回到最初的车道。从左到右改变车道的时间点由参与者决定。遵循德国的交通规则，只允许从左车道超车。共招募了9名年龄介乎25至38岁的参与者。他们都持有有效的驾驶执照。每位参与者进行了约25分钟的驾驶。

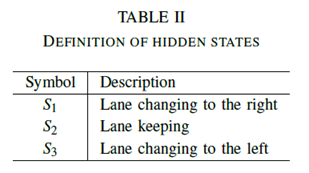
1）数据处理阶段：为了将数据标记为隐藏状态序列以及观察序列，需要对信号数据进行分类和处理。此贡献中的隐藏状态仅考虑更改车道。在驾驶模拟中，可以通过车辆中心点的位置确定当前车道i。因此，通过在不同时间比较车道i的值，可以确定车辆的车道变换。当当前车道的值与最后时刻it-1相同时，定义车道保持。当该值增加时定义向左变换的车道，并且当减小车道时向右变换车道。在实验中，驾驶员决定改变车道（转向灯）的时间已经在车道变换之前的2到3秒之间，平均值为2.5秒。因此，将考虑在行动之前2.5秒发生作为驾驶行为的车道变化。然而，如果自我车辆通过驾驶与白线重叠，则可能产生一些车道变换数据，并且这些数据不反映驾驶员的真实行为。因此，有必要去除这些干扰数据以获得准确的实验数据。表II给出了每种隐藏状态的符号及其具体描述。

观察载体可以通过预滤器分类并处理成序列。如第II部分所述，将使用最大ACC，最大DR以及最小FAR确定最佳预滤波器。因此，它应该用于改善驾驶行为预测的性能。为了证明这一点，使用两个不同的预滤器对观察向量进行分类。一个预过滤器正在使用这些最佳段。另一种是使用一组通用分段范围进行比较，通过比较实验数据给出，例如平均值，最小安全距离等。

2）训练阶段：在本实验中，每个实验数据集分为10个子集，这10个子集中的7个被认为是训练数据集，其他被认为是测试数据集。每个训练数据集的位置是不同的，并且不重复，例如，第一训练数据集从第一至第七子集中选择，第二训练数据集从第二至第八子集中选择，依此类推。每个训练和测试数据集必须包含不同的换道操作。训练数据集可用于估计HMM参数。利用该HMM参数，可以计算隐藏状态。在下一步骤中，将比较来自训练数据的隐藏状态序列和由HMM模型计算的隐藏状态序列，以检查对应关系并计算ACC，DR和FAR。然后，计算目标函数（7）。然后，通过关于上述目标函数的优化来定义预滤波器值。该预滤器及其相应的HMM模型将用于测试阶段。

3） 测试阶段：每个特定于驱动程序的测试数据集必须与在训练阶段使用的数据相关。 因此，已经在训练阶段计算了每个测试数据集的最佳预滤波器和相应的HMM模型。最可能的驾驶行为将通过使用相应的HMM来确定。通过计算和实际驾驶行为之间的比较，可以评估准确性。

B评估

为了评估所提出的方法，将通过使用相同的训练数据集和不同的预滤波器来学习HMM。在选择最佳预滤器之后，使用通用预滤器与最佳预滤器比较该方法。将比较计算的和实际的驾驶行为以评估相似性。数据集＃5的测试阶段的结果如图5所示。这里隐藏状态（驾驶行为）作为模拟时间的函数给出。隐藏状态的符号如表II所示。绿色，蓝色和红色线分别表示使用一般预滤波器的原始状态，计算的隐藏状态，以及使用最佳预滤波器计算的隐藏状态。结果表明，优化的基于预过滤器的HMM预测的状态最适合原始状态。蓝线错误计算隐藏状态的数量多于红色。

图5. HMM验证结果[测试数据集＃5]

通过选择数据集＃5的一般和最佳预滤波器的ACC，DR和FAR的百分比示于表III中。从得到的结果可以清楚地看出，使用最佳预滤器，总体ACC分别从73.4％（训练）和68.8％（测试）增加到91.9％和87.5％。类似地，使用最佳预滤器，DR高于使用通用预滤器。

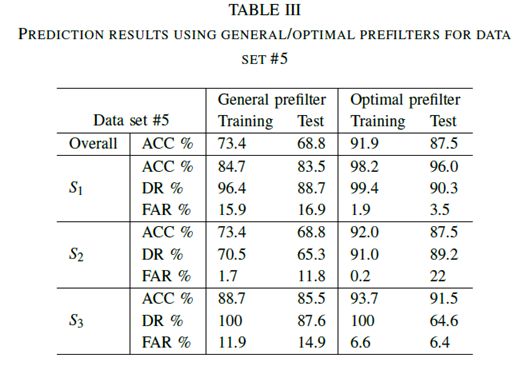
在三种不同演习的FAR中，右侧车道变换的训练和测试阶段的FAR分别为15.9％和16.9％，优化后，FAR降至1.9％和3.5％。FAR的值可以由等式（6）定义。可以看出，较高的FAR值是由图3中定义的较高的分子FP值（假阳性）产生的。对于向右变化的机动车道，FP是真实状态时的事件数，估计的状态是右边的车道变换。这些结果也可以从图5中检测到。这里S1定义了向右的车道变换。可以观察到，在若干情况下，估计的状态被错误地计算为S1。上述描述性问题更常出现在蓝线（使用一般预滤波器）而不是红线（使用最佳预滤波器）。可以得出结论，使用合适的预滤器可以改善预测结果。即使通过，在实验期间仍然可以找到一些例外，例如，车道保持（测试）的优化FAR值比预设值（大约高10％）更差。然而，考虑到所有情况的总体结果由于预滤器的优化而得到改善。

图6. 9个测试数据集的平均ACC、DR和FAR由不同模型实现

为了验证模型在驾驶行为预测方面的有效性，使用其他算法进行比较。人工神经网络（ANN）和支持向量机（SVM）等典型算法用于建立驾驶行为模型。在[17]中，作者建立了三个模型，包括ANN，SVM，组合ANN和SVM（ANN-SVM）来估计公路车道下降时的车道变换行为。这两种算法的优点是它们不需要数据处理。为了评估这些方法，将实际驾驶行为与所有数据集的估计驾驶行为进行比较。然后，计算每个驾驶行为的ACC，DR和FAR。每组的相应速率如图6所示。从结果（图6）可以说，在预滤波器的最佳选择之后，所有ACC，DR以及（1-FAR）值都较大超过80％。尽管仍然可以找到一些例外，例如ANN-SVM（保守）的一些ACC高于最佳HMM，但是DR的值减小。为了进一步评估驾驶行为预测的性能，接收器操作特性（ROC）图如图7所示。从结果可以看出，使用最优HMM，DR最高，FAR最低。方法。因此，最佳HMM在所有模型中都具有最佳性能。

图7.不同模型的ROC图

IV.总结和结论

在该研究中，基于隐马尔可夫模型( HMM )开发了一个驾驶行为预测模型。包括左/右车道变换和车道保持在内的三种不同的驾驶动作被建模为HMM的隐藏状态，并使用驾驶模拟器在高速公路场景中进行模拟。基于HMM，可以通过观察状态推断出不可观察的状态。所考虑的方法基于这样的假设，即相关的物理变量被离散成若干段，以考虑典型的传感器特性。通过寻找最佳预滤波器，而不是优化HMM模型，考虑并改进了HMM的预测性能。在该方法中，基于从9个不同测试驱动程序获得的数据，验证了该方法。每次都选择不同位置的子集进行训练和测试。在相同的实验数据集上，使用观察段范围的一般(预先设置的)值和最终(优化的)值来比较HMM模型。

最终获得的结果显示HMM识别驾驶员行为的能力显著提高。结果表明，除了分类器（这里：HMM ）之外，组合的预设和适应策略对该方法的统计特性有显著影响。使用最佳参数的HMM模型提高了检测率和准确性，同时降低了误报率。通过选择最佳预过滤参数，预测性能可以得到改善，这一点已在该研究中得到成功证明。