

详细介绍概率模型SLAM方法中的卡尔曼滤波
描述
在智能服务机器人逐渐成为行业风口浪尖的今天,移动机器人的身影越来越多地出现在人们身边。相信随着传感技术、智能技术和计算技术等的不断提高,智能移动机器人一定能够在生产和生活中融入人类生活中。上一期小编大致介绍了基于概率模型的SLAM方法的基本原理,本期,小编给大家详细介绍下概率模型SLAM方法中一个比较重要的家族:卡尔曼滤波。
什么是卡尔曼滤波
卡尔曼滤波(Kalman filtering),又称线性二次型估计(Linear quadratic estimation),是Swerling(1958)和Kalman(1960)作为线性高斯系统中的预测和滤波技术而提出的。
最早由Stanley Schmidt首次实现,后被Kalman发掘并应用于NASA的阿波罗计划。提到阿波罗计划,大家可能会有种小编是在帮卡尔曼滤波蹭“人类登月”热度的感觉,其实不然,在工程领域里,卡尔曼滤波一样也很“高大上”。
作为线性高斯系统预测方法中最优、最高效的工具,卡尔曼滤波器及其变种已经被广泛应用在诸如机器人导航,传感器数据融合,导弹追踪,人脸识别等多种领域近半个世纪。
卡尔曼滤波解决的问题是“线性高斯系统的预测和滤波”,那么什么是线性高斯系统呢?高斯分布想必大家应该都有所耳闻,或者换个说法,正态分布,这个高中经常被数学老师拿来让我们估算人群身高分布的“大杀器”。它的长相是下图这个样子的:
正态分布很简单,只需要两个参数就可以表示了,即期望μ和方差σ。一个多元正态分布的表达式为:
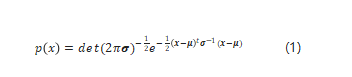
呃,上面的公式看看就好,其实只需要知道正态分布的期望μ就是它的对称轴,方差σ就是它的“胖瘦”情况,上面的图中给出了几个不同μ和σ的正态分布的样子。一个所谓的“高斯线性系统”需要满足三个条件:
1)状态转移概率p(xt|ut,xt-1)是带有随机高斯噪声的线性函数;
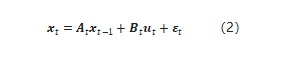
xt是t时刻的状态向量,它是上一时刻的状态xt-1和当前时刻的控制量ut的线性组合,εt表示一个随机的高斯噪声,它是由状态转移引入的不确定性。需要注意的是,式2表达的不是一个确定的解,而是一个分布,它由期望Atxt-1+Btut和方差rt确定。
2)测量概率p(zt|xt)也与带有高斯噪声的状态量呈线性关系;
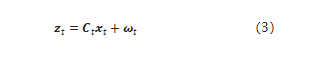
zt是t时刻的测量向量,ωt是测量时的高斯噪声。同样,式3也是一个分布,期望是Ctxt,方差是qt。
3) 初始置信度bel(x0)也是正态分布的,它期望是μ0方差是σ0。
如果一个系统能满足上述三个条件,则它的后验估计也满足高斯分布,其期望为μt方差为σt。换句话说,一个最优估计的问题,它的先验概率分布是高斯分布,同时它的测量概率分布也是高斯分布,那么它的后验概率也满足高斯分布,并可求它的期望和方差。
下面拿擎朗智能第三代系列机器人——peanut举个例子,一辆做匀速运动的peanut,它的初始位置为s0,速度为v,求它在t时刻的位置,大家一定立马就能给出答案:st=s0+vt。
没错,理论上t时刻的位置就应该是这个值。但在实际工程应用中,位置s和速度v并不会是理想值,它会有一定的不确定性,我们假设这个不确定性是满足高斯分布的。
如果没有后验的话,这个不确定性会不断地叠加,就如上图(a)所示,随着peanut的不断前行,位置s概率分布的方差会越来越大,peanut对自己位置的估计也就越来越不准确。
为了确保位姿估计的准确性,加入了一个观测值去修正计算得到的速度,例如用里程计去测量每次走过的距离st’,如上图(b)所示,
蓝色表示peanut当前时刻的先验估计,它由上一时刻的估计值st-1通过运动方程求得;
绿色表示从里程计获得的观测值得概率分布,它与先验估计有一定的偏差;
紫色表示通过卡尔曼滤波后,修正的概率分布。
从滤波的结果来看,后验估计也是高斯分布,它的分布综合了先验和观测的期望,且缩小了方差。
卡尔曼滤波的一般步骤
通过上面的介绍,相信大家对卡尔曼滤波能干啥应该有个大致的了解了,那么它是如何使用的呢?废话不多说,先上公式,
卡尔曼滤波的经典五步:
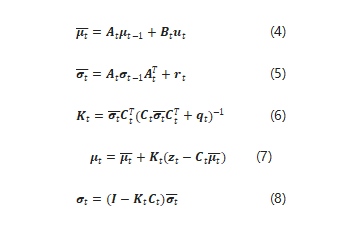
好吧,看到上面的公式大家可能会有点懵,下面小编尽量用比较通俗的语句解释下,
这五步具体做了什么:
1) 计算状态转移的期望,μt-1表示上一状态的期望值,其实就是上一次后验分布的期望,ut是控制量,这样就求出了先验概率分布的期望值;
2) 光有期望值还不够,还需要计算方差才能得到一个完整的正态分布,公式5就是计算先验概率方差的过程,其中σt-1表示上一次后验的方差,rt是状态转移引入高斯噪声的方差。
3) 得到先验概率分布后,就需要通过贝叶斯估计求解后验概率分布。公式6是求解卡尔曼增益K,它通过观测概率分布的方差qt和先验概率分布的方差求得。
4) 卡尔曼增益K主要用来衡量“预测值”和“观测值”的比重,即是更相信预测的结果还是更相信观测的结果;具体表现在公式7,后验的期望是先验的期望加上卡尔曼增益乘以估计和观测期望的偏差。
5) 后验的期望得到后,再通过公式8更新后验的方差,就得到了后验估计得概率分布。
通过上述五步就精确地求解了一个“线性高斯系统”的后验估计,算法里运算量最大的矩阵求逆运算和矩阵乘法运算时间复杂的分别可近似为O(k2.4)和O(k2),k是矩阵维度。相对其他算法,卡尔曼滤波算法是相当高效的。
卡尔曼滤波的变种
卡尔曼滤波虽然高效且精确,但是他有个致命的缺陷,即要求系统是高斯线性的,而实际应用中,绝大多数系统不是高斯线性的。
于是就有了所谓的扩展卡尔曼滤波EKF(Extended Kalman Filter)和无迹卡尔曼滤波UKF(Unscented Kalmen Filter )的变种。
EKF和UKF都是将实际状态转移模型局部线性化,只不过前者采用的是泰勒展开进行线性化,而后者采用的是通过加权统计线性回归过程实现随机线性化。
通俗的讲,EKF是计算非线性函数的切线来进行线性化的,因此EKF需要知道状态转移方程的雅可比矩阵(Jacobian Matrix),UKF则是通过提取所谓的δ点,用这些δ点拟合的直线作为局部线性化的参考,δ的取值与分布的协方差有关。
EKF和UKF的算法复杂度近似,一般情况下EKF会稍微快一点,而估计的结果一般情况下UKF要优于EKF。
卡尔曼滤波作为经典的估计算法,被广泛应用在各个领域之中,在机器人领域里,卡尔曼滤波主要应用在多传感器融合,SLAM的最优估计等问题中。
以上就是本期关于卡尔曼滤波的内容,下期小编将给大家介绍粒子滤波的相关内容。
-
卡尔曼滤波器介绍2008-07-14 13520
-
项目应用中的卡尔曼滤波2019-05-22 1162
-
请问有加速度计的卡尔曼滤波C代码吗2019-07-09 2744
-
新手平衡小车的卡尔曼滤波算法总结2022-05-11 659
-
动态定位中的卡尔曼滤波研究2017-05-24 1116
-
基于多维影响因子的卡尔曼滤波算法2017-12-29 1082
-
使用51单片机实现MPU6050的卡尔曼滤波算法代码免费下载2019-08-20 1900
-
卡尔曼滤波器及其工程应用的详细资料说明2019-07-25 1450
-
几种最优估计和卡尔曼滤波原理的学习课件免费下载2020-05-09 1025
-
多旋翼飞行器设计与控制的卡尔曼滤波器2021-09-14 975
-
扩展卡尔曼滤波的原理2022-08-12 7061
-
卡尔曼滤波(KF)与扩展卡尔曼(EKF)2023-05-10 831
-
浅析卡尔曼滤波2023-06-14 2900
-
卡尔曼滤波的数学基础2023-08-30 1540
-
卡尔曼滤波家族2024-01-14 2019
全部0条评论

快来发表一下你的评论吧 !

