

AI智能体学习如何跑步、躲避跨越障碍物
电子说
描述
AI智能体学习如何跑步、躲避跨越障碍物
近年来,深度学习受到全球关注。成就最为突出的便是深度强化学习,例如Alpha Go等。本文作者Artem Oppermann基于此,对深度强化学习训练AI智能体所需要的数学背景知识——马尔科夫链做了深入浅出的介绍。
近年来,世界各地的研究员和媒体对深度学习极其关注。而深度学习方面成就最为突出的就是深度强化学习——从谷歌Alpha Go击败世界顶级棋手,到DeepMind的AI智能体自学走路、跑步以及躲避障碍物,如下图所示:
图2:AI智能体学习如何跑步、躲避跨越障碍物
图3:AI智能体学习如何跑步、躲避跨越障碍物
还有一些AI智能体打破了自2014年以来人类玩家在雅达利游戏中的最高纪录。
图4:AI智能体学习如何玩儿雅达利游戏
而这一切最令人惊奇的是这些AI智能体中,没有一个是由人类明确编程或者指导他们如何完成这些任务的。他们仅仅是通过深度学习和强化学习的力量在自学!
本文作者Artem Oppermann在Medium中开设了《自学AI智能体》的“连载”课程,本文是其第一篇文章,详细介绍了AI智能体自学完成任务这一过程背后需要了解的数学知识——马尔可夫链。
Nutshell中的深度强化学习
深度强化学习可以概括为构建一种算法(或AI智能体),直接从与环境的交互中学习。
图5:深度强化学习示意图
环境可以是真实世界,电脑游戏,模拟,甚至棋盘游戏,比如围棋或象棋。就像人类一样,人工智能代理人从其行为的结果中学习,而不是从明确的教导中学习。
在深度强化学习中,智能体是由神经网络表示的。神经网络直接与环境相互作用。它观察环境的当前状态,并根据当前状态和过去的经验决定采取何种行动(例如向左、向右移动等)。根据采取的行动,AI智能体收到一个奖励(Reward)。奖励的数量决定了在解决给定问题时采取的行动的质量(例如学习如何走路)。智能体的目标是学习在任何特定的情况下采取行动,使累积的奖励随时间最大化。
马尔可夫决策过程
马尔可夫决策过程(MDP)是一个离散时间随机控制过程。
MDP是迄今为止我们对AI智能体的复杂环境建模的最佳方法。智能体要解决的每个问题都可以看作是S1、S2、S3、……Sn(状态可以是围棋/象棋的棋局配置)的序列。智能体采取行动并从一个状态移动到另一个状态。
马尔可夫过程
马尔可夫过程是一个描述可能状态序列的随机模型,其中当前状态仅依赖于以前的状态。这也被称为马尔科夫性质(公式1)。对于强化学习,这意味着AI智能体的下一个状态只依赖于最后一个状态,而不是之前的所有状态。

公式1:马尔可夫性质
马尔可夫过程是一个随机过程。这意味着从当前状态s到下一个状态s'的转变“只能在一定概率下发生”(公式2)。在马尔科夫过程中,一个被告知向左移动的智能体只会在一定概率下向左移动,例如0.998。在概率很小的情况下,由环境决定智能体的最终位置。

公式2:从状态s到状态s'的转变概率
Pss '可以看作是状态转移矩阵P中的一个条目,它定义了从所有状态s到所有后续状态s'的转移概率(公式3)。

公式3:转移概率矩阵
马尔可夫奖励(Reward)过程
马尔可夫奖励过程是一个元组

公式4:在状态s中期望获得奖励
总奖励Gt(公式5),它是智能体在所有状态序列中所获得的预期累积奖励。每个奖励都由所谓的折扣因子γ∈[0,1]加权。

公式5:所有状态的奖励总额
价值函数(Value Function)
另一个重要的概念是价值函数v(s)中的一个。价值函数将一个值映射到每个状态s。状态s的值被定义为AI智能体在状态s中开始其进程时将得到的预期总奖励(公式6)。

公式6:价值函数,从状态s开始的期望返回值
价值函数可以分解为两个部分:
处于状态s时,智能体收到的即使奖励(immediate reward)R(t+1);
在状态s之后的下一个状态的折现值(discounted value)v(s(t+1));

公式7:价值函数的分解
贝尔曼方程
马尔可夫奖励过程的贝尔曼方程
分解后的值函数(公式8)也称为马尔可夫奖励过程的贝尔曼方程。
该函数可以在节点图中可视化(图6),从状态s开始,得到值v(s)。在状态s中,我们有特定的概率Pss '到下一个状态s'中结束。在这种特殊情况下,我们有两个可能的下一个状态为了获得值v(s),我们必须总结由概率Pss'加权的可能的下一个状态的值v(s'),并从状态s中添加直接奖励。 这就产生了公式9,如果我们在等式中执行期望算子E,那么这只不是公式8。

公式8:价值函数分解

图6:从s到s'的随机转变

公式9:执行期望算子E后的贝尔曼方程
马尔可夫决策过程——定义
马尔可夫决策过程是一个有决策的马尔可夫奖励过程。
马尔可夫决策过程是马尔可夫奖励过程的决策。 马尔可夫决策过程由一组元组

公式10:期望奖励取决于状态s中的行为
策略
在这一点上,我们将讨论智能体如何决定在特定状态下必须采取哪些行动。 这由所谓的策略π(公式11)决定。 从数学角度讲,策略是对给定状态的所有行动的分配。 策略确定从状态s到智能体必须采取的操作a的映射。

公式11:策略作为从s到a的一个映射
该策略导致状态价值函数v(s)的新定义(公式12),我们现在将其定义为从状态s开始的预期返回,然后遵循策略π。

公式12:状态值函数
动作价值函数
除状态值函数之外的另一个重要功能是所谓的动作值函数q(s,a)(公式13)。 动作值函数是我们通过从状态s开始,采取行动a然后遵循策略π获得的预期回报。 请注意,对于状态s,q(s,a)可以采用多个值,因为智能体可以在状态s中执行多个操作。 Q(s,a)的计算是通过神经网络实现的。 给定状态作为输入,网络计算该状态下每个可能动作的质量作为标量(图7)。 更高的质量意味着在给定目标方面采取更好的行动。

图7:动作价值函数说明
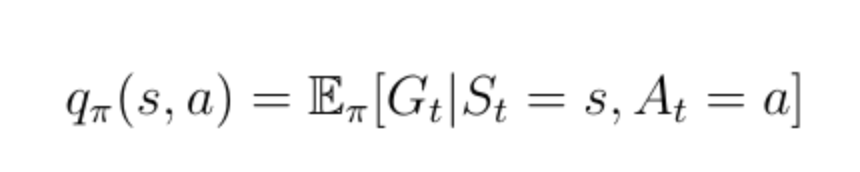
公式13:动作价值函数
状态值函数v(s)可以分解为以下形式:

公式14:状态价值函数分解
同样的分解也适用于动作价值函数:

公式15:动作价值函数分解
在这一点上,我们讨论v(s)和q(s,a)如何相互关联。 这些函数之间的关系可以在图中再次可视化:

图8:v(s)和q(s,a)之间关系的可视化
在这个例子中,处于状态s允许我们采取两种可能的行动a,根据定义,在特定状态下采取特定的行动给了我们动作值q(s,a)。价值函数v(s)是概率q(s,a)的和,由在状态s中采取行动a的概率来赋予权重。

公式16:状态值函数是动作值的加权和
现在让我们考虑图9中的相反情况。二叉树的根现在是一个我们选择采取特定动作的状态。 请记住,马尔可夫过程是随机的。 采取行动并不意味着你将以100%的确定性结束你想要的目标。 严格地说,你必须考虑在采取行动后最终进入其他状态的概率。 在采取行动后的这种特殊情况下,你可以最终处于两个不同的下一个状态s':

图9:v(s)与q(s,a)关系的可视化
为了获得动作值,你必须用概率加权的折现状态值来最终得到所有可能的状态(在本例中仅为2),并加上即时奖励:
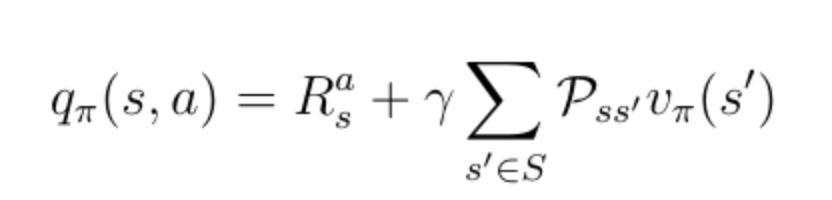
公式17:q(s,a)和v(s)之间的关系
既然我们知道了这些函数之间的关系,我们就可以将公式16中的v(s)插入公式17中的q(s,a)中。我们得到公式18,可以看出当前的q(s,a)和下一个动作值q(s,a)之间存在递归关系。

公式18:动作值函数的递归性质
这种递归关系可以再次在二叉树中可视化(图10)。
图10:q(s,a)递归行为的可视化
-
遇到障碍物自动返回?2011-09-10 0
-
强悍版智能小车2012-03-09 0
-
设计完PCB后走线不能躲避障碍物时什么情况2012-12-20 0
-
求教 障碍物感应类开关2013-03-07 0
-
越障小车电机、轮胎选择2013-04-03 0
-
智能壁障车2013-10-26 0
-
基于AT89S52芯片的简易智能小车的设计2014-10-31 0
-
遇障碍物时 语音提示 前方危险,请注意。2017-02-24 0
-
基于labview机器视觉的障碍物时别2017-03-14 0
-
新人求教AD中Pullback(障碍物)到底是一个什么概念或作用?2017-11-04 0
-
ANYmal机器人具有腿和脚,可跨越障碍物2021-08-30 0
-
障碍物检测实验2009-03-23 2861
-
障碍物方位检测实验2009-03-23 2005
-
猎豹机器人配备新的算法_没有摄像头也可以躲避障碍物?2018-07-08 3241
-
嵌入式AI新技术助力无人机躲避移动障碍2019-06-13 1003
全部0条评论

快来发表一下你的评论吧 !

