

捷联惯导系统中Allan方差的使用要点
今日头条
描述
1. Allan方差分析主要用于分析陀螺量化噪声、角度随机游走噪声(角速率白噪声)、零偏不稳定性、角速率随机游走(角加速度白噪声)和速率斜坡(角速率常值趋势项),等五种典型误差。有些文献也提到可用于分析周期项和一阶马尔可夫误差,但这不是Allan方差分析的强项,周期项更适合用功率谱分析,马尔可夫更适合于用相关分析(时间序列分析),不要试图以己之短攻人所长!
以上文章摘自严老师博客

2. Allan方差分析的是静态误差,陀螺必须在静基座下进行采集数据,否则要是动基座下采集的陀螺数据,分析的结果到底是陀螺误差呢还是基座运动特性?!
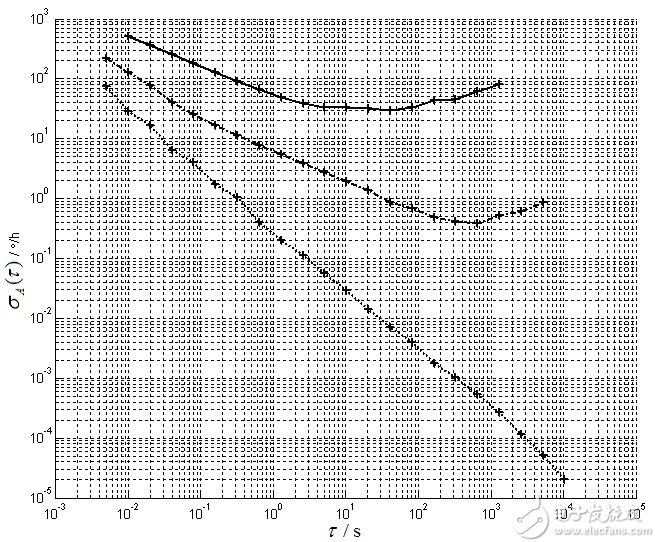
3. Allan方差计算中采用了“差分”计算操作,因此Allan方差无法分析获得陀螺随机常值漂移参数。若是将几个陀螺的Allan方差曲线同时绘制在同一个双对数图上,曲线在左下角的对应的陀螺性能一般较好些,而右上角的差些。如下图从下到上分别为激光陀螺、光纤陀螺和MEMS陀螺,其中激光陀螺性能最好。如果是同一类型的陀螺,也是左下角的曲线性能稍好些。
4. Allan方差可用于分析五种典型误差,但是某个陀螺中并不一定五种误差都有同时表现出来,不画Allan方差图/不肉眼看图,而盲目的采用最小二乘回归方法强行地就想求解五个系数的人是典型的教条主义者,往往得不到好的结果。比如如下Allan方差图中y曲线所示,采用“三段论”大概读图计算角度随机游走系数、零偏不稳定性和角速率随机游走(或速率斜坡)即可,完全可满足实际应用。过细分析想得出精确系数的人都是有洁癖的。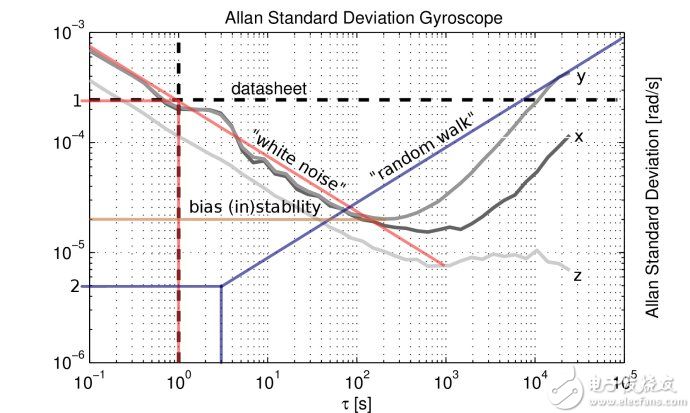
5. 如下图红圈中的Allan方差并不是什么马尔可夫过程噪声的,往往是由于陀螺经过低通滤波器后造成的,这时Allan方差反映的是滤波器的特性,而不是实际陀螺的特性。因此要得到陀螺的本质特性,应该对陀螺作高频采样,并且不能对原始数据做任何处理,直接用Allan方差分析才行。

6. Allan方差分析的一个用途是分析陀螺的性能或对比不同陀螺的性能,如前3所述,相比于其它分析法Allan法还是很好用的,比较全面。另一个用途是获得噪声参数,用于组合导航的Kalman滤波噪声参数设置。不是所有的Allan方差噪声系数都有用,主要有用的是角度随机游走系数(用于设置Q阵)和零偏不稳定性系数(用于设置一阶马氏过程的方差),其实这两个系数量级大小差不多就行了,太精细也没用。毕竟Allan方差分析的只是一个样本,你再采一个样本试试,肯定会有差异的;此外采集的是陀螺的静态性能数据,鬼知道实际动态应用的时候陀螺误差会变化多大,存在数量级差别都很有可能。这里需要的是理论指导下的工程和经验,而不是教条主义。
7. 老外给MEMS陀螺指标喜欢用Allan方差,也就是Allan方差图的最低点,比如下图stim202,说该陀螺精度是0.5deg/h。其实国内喜欢用10s平滑结果,从图中直接读10s对应的大概是4deg/h。数值“0.5deg/h”表面看着挺振奋的,实际不要被它迷惑,它对应的时间横坐标是3000s多,谁用陀螺也不会静止这么长时间!而且该误差是一次启动稳定性,而不是逐次启动重复性,也许该陀螺逐次重复性有可能几十甚至上百deg/h。使用该陀螺在静态下是不能找北的,不要被“0.5deg/h”迷惑。当然在目前MEMS陀螺世界中,stim202性能还是相对很优秀的。

8. 如果画出的Allan方差图形不像典型的U型或V型图,极端如下,不要感觉到诧异,也不要再试图用Allan方差去分析它(又是教条主义),没意义!此时Allan分析失效,应试图对原始数据作分析和解释。
仿真Matlab程序:
y = randn(100000,1) + 0.00001*[1:100000]';
y(20000:50000)=sin(0.01*[20000:50000]);
y(70000:90000)=y(70000:90000)-0.00002*[70000:90000]';
[sigma, tau, Err] = avar(filter(ones(5,1), 1, y), 0.1);
9. Allan方差分析理论可参见《惯性仪器测试与数据分析》第八章,程序可见psins工具箱中的avar函数,用不着太复杂的计算方法。
- 相关推荐
- 热点推荐
-
LABVIEW 怎么实现Allan方差分析?2025-09-03 5609
-
如何采用渐消卡尔曼滤波器防止捷联惯导系统滤波发散2009-05-30 1054
-
高精度游移方位捷联惯导系统的数字仿真2009-06-21 962
-
捷联惯导系统中微机械陀螺测试参数的分析与标定2016-12-17 919
-
MEMS传感器的捷联惯导系统设计中的应用2017-11-29 1470
-
捷联惯导系统中Allan方差的使用要点 分析2018-10-30 2611
-
基于TMS320C5410和ADuC834微处理器实现压电捷联惯导系统的设计2020-04-22 1861
-
基于触摸屏和RS-232串口实现捷联惯导显控系统的设计2021-03-29 4285
-
MEMS陀螺捷联惯导系统标定方法综述2021-08-05 1602
-
陀螺捷联惯导系统标定2022-07-04 561
-
Allan 方差理论及测量方法2024-06-07 3828
全部0条评论

快来发表一下你的评论吧 !

