

数据科学家需要知道的5个基本统计概念,如何才能最有效地应用它们
电子说
描述
对于数据科学的艺术,统计学可以说是一个强大的工具。从高层次的角度来看,统计是利用数学对数据进行技术分析。一个基本的可视化,如条形图,可以给你提供一些高级的信息,但是通过统计学,我们可以以一种更加以信息驱动和更有针对性的方式来操作数据。所用到的数学方法能帮助我们对数据形成具体的结论,而不是去靠猜测。
通过使用统计学,我们可以更深入、更细致地了解我们的数据到底是如何构造的,并基于这种结构,我们如何最佳地应用其他数据科学技术来获取更多的信息。现在,我们来看看数据科学家们需要知道的5个基本统计概念,以及如何才能最有效地应用它们!
统计特征
统计特征可能是数据科学中最常用的统计概念。这通常是你在研究数据集时应用的第一种统计技术,包括偏差、方差、平均值、中位数、百分位数等。这一切都相当容易理解并在代码中实现!看看下面的图表。
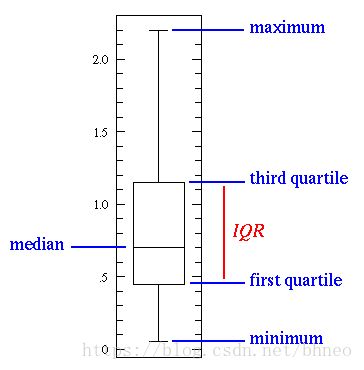
一个简单的箱型图
中间的那条线是数据的中位数。由于中位数对离群值的鲁棒性更强,因此中位数比平均值用得更多。第一个四分位数本质上是第25百分位数,表示数据中25%的点低于这个值。第三个四分位数是第75百分位数,表示数据中75%的点都低于这个值。最小值和最大值表示数据范围的上、下端。
一个箱型图完美地阐述了我们能用基本统计特征做什么:
当框图很短时,它意味着许多数据点是相似的,因为在小范围内有许多值
当框图很长时,它意味着许多数据点是完全不同的,因为这些值分布在一个较广的范围内
如果中值更接近底部,那么我们知道大多数数据的值更低。如果中值更接近顶部,那么我们知道大多数数据都有更高的值。基本上,如果中值线不在方框中间,那么它就表示数据有偏斜。
是否有长尾?这意味着你的数据有很高的标准差和方差,说明这些值是分散的,高度不同。如果你在盒子的一边有长尾而在另一边没有,那么你的数据可能只在一个方向上有很大的变化。
所有这些信息都来自一些简单的统计特征,并且很容易计算!当你需要对数据进行快速而有效的查看时,请尝试这些方法。
概率分布
我们可以将概率定义为某个事件发生的概率百分比。在数据科学中,通常在0到1之间进行量化,0表示我们确信不会发生,1表示我们确信它会发生。概率分布是一个函数,表示实验中所有可能值的概率。请看下面的图表。
均匀分布是我们在这里展示的3个分布中最基本的。它只有一个值,这个值只出现在某个范围内,而超出这个范围的任何值都是0。这在很大程度上是一种“开关”分布。我们也可以把它看作是一个有两个类别的分类变量:0或其他值。你的分类变量可能有多个非0的值,但我们仍然可以把它想象成多个均匀分布的分段函数。
正态分布,通常被称为高斯分布,由均值和标准差定义。均值在空间上平移分布,标准差控制分散程度。与其他分布的重要区别(比如泊松分布)是,其所有方向上的标准差都是一样的。因此,对于高斯分布,我们知道数据集的平均值以及数据的发散程度(例如,它是广泛分布的还是高度集中在少数几个值)。
泊松分布与正态分布相似,但增加了偏斜因子。在偏态值较低的情况下,泊松分布会像正态分布一样向各个方向均匀发散。但当偏度值较大时,我们的数据在不同方向的发散会不同;在一个方向,它将非常分散,在另一个方向,它将高度集中。
虽然有很多的分布可以深入研究,但这3个已经给我们带来了很多价值。我们可以用均匀分布快速地看到和解释分类变量。如果我们看到一个高斯分布便知道有很多算法在默认情况下都能很好地处理高斯分布,所以我们应该这样做。有了泊松分布,我们会发现必须特别小心选择一种对空间发散的变化具有鲁棒性的算法。
降维
降维这个术语很容易理解。我们有一个数据集,希望减少它的维数。在数据科学中,它是特征变量的数量。请看下面的图表。
降维
立方体代表我们的数据集,它有三个维度,总共有1000个点。虽然1000个点的计算在今天很容易处理,但是对于更大的范围我们仍然会遇到问题。然而,仅仅从二维的角度来看我们的数据,例如从立方体的一边,我们可以看到,从这个角度划分所有的颜色是很容易的。通过降维,我们可以将三维数据投射到二维平面上。这有效地将我们需要计算的点数减少了100,大大节省了计算量!
另一种降维方法是特征剪枝。有了特征剪枝,我们可以删除对分析不重要的任何特征。例如,在研究数据集之后,我们可能会发现,在10个特性中,有7个特性与输出的相关性很高,而其他3个特性的相关性很低。那么,这3个低相关特性可能不值得计算,不过我们只能根据分析在不影响输出的情况下将它们删除。
当前用于降维的最常见的技术是PCA,它本质上是创建了特征的向量表示,显示它们对输出有多重要,比如他们的相关性。PCA可以用于上面讨论的两种降维方式。在此教程中可以了解到更多信息。
过采样与欠采样
过采样和欠采样是用于分类问题的技术。有时,我们的分类数据集可能会严重倾斜到一边。例如,类1有2000个样本,但类2只有200个。这将对很多我们常用于建模并预测的机器学习技术带来影响!但过采样和欠采样可以与之对抗。请看下面的图表。
欠采样与过采样
在上图的左边和右边,我们的蓝色类比橙色类拥有更多的样本。在这种情况下,有两个预处理选项可以帮助我们的机器学习模型的训练。
欠采样意味着我们将只从多数类中选择一部分数据,只使用与少数类样本数相同的数量。这个方案应当保证采样后类别的概率分布与之前相同。操作很容易,我们只是通过取更少的样本来平衡数据集!
过采样意味着我们将创建少数类的副本,以便拥有与多数类相同的样本。创建副本时应当保证少数类的分布不变。这个方案中,我们只是把我们的数据集变得更均衡,并没有得到更多的数据!
贝叶斯统计
为了充分理解为什么我们要使用贝叶斯统计,需要首先了解频率统计不足的地方。频率统计是大多数人听到“概率”这个词时会想到的统计方法。它应用数学来分析某些事件发生的概率,具体来说,我们使用的数据都是先验的。
我们看一个例子。假设给你一个骰子然后问你掷出6的概率是多少,大多数人会说1 / 6。确实,如果我们做频率分析,会通过一些数据比如某人掷骰子10000次,然后计算每个数字出现的频率;大概是1 / 6!
但如果有人告诉你,给你的那个骰子是被改造过的并且落地后总会是6的那面朝上呢?频率分析只考虑了先验的数据,并没有考虑骰子被改造过这个因素。
贝叶斯统计确实考虑到了这个问题,可以用贝叶定理来说明这一点:
贝叶斯定律
方程中的概率P(H)基本上就是频率分析;表示根据之前的先验数据,事件发生的概率是多少。方程中的P(E|H)被称为似然,本质上是根据频率分析得到的信息的条件下,我们得到的结论是正确的概率。例如,滚动骰子10000次,而前1000次全部得到6,你会开始肯定,骰子是被改造过的!P(E)是实际结论成立的概率。如果我告诉你,骰子是改造过的,你能相信我并说它是真的吗?
如果我们的频率分析很好那么就会有一定的权重说明:是的,我们对6的猜测是正确的。与此同时,我们考虑了改造骰子的事实,它是否为真,同时基于它自己的先验和频率分析。从方程的布局可以看出,贝叶斯统计考虑了所有的因素。当你觉得之前的数据不能很好地代表未来的数据和结果时,就使用它。
-
TI科学家谈浮点DSP未来发展2009-11-03 9445
-
科学家研制可在黑暗中使用的细菌发电生物电池2013-12-03 3328
-
美科学家建新设备将光束变固体 可用于研制量子计算机2014-09-28 3735
-
美科学家推出多种波动描记传感器2018-10-24 2339
-
如何有效地盘活闲置的频谱资源?2019-08-02 1671
-
AI人才炙手可热 数据科学家和机器学习工程师出现大缺口2018-03-03 1168
-
通往数据科学家的崎岖道路2018-07-26 3123
-
哪些才是对数据科学家最迫切的技能呢?2018-11-19 3532
-
什么是数据科学家?需要认证吗?2019-02-14 7288
-
数据科学家与机器学习工程师怎么区分2019-05-18 3906
-
数据科学家常犯的10个编程错误2019-05-24 3113
-
采访资深数据科学家:成为数据科学家应具有的品质2020-06-30 2851
-
什么是数据科学家的最佳编程语言?2020-07-05 3007
-
深入研究数据科学家使用的常见统计和分析技术2021-01-14 2422
-
面向工程师和科学家的大数据2022-10-06 1151
全部0条评论

快来发表一下你的评论吧 !

