GBM算法的历史和原理

编者按：DM Labs创始人、DIGINETICA首席数据官Alexey Natekin讲解了梯度提升算法的原理。

大家好！目前为止，我们已经介绍了从探索性分析到时序分析在内的9个主题。今天我们将介绍最流行、最实用的机器学习算法之一：梯度提升。

概览

导言和梯度提升的历史

GBM算法

损失函数

相关资源

导言和梯度提升的历史

在机器学习领域，梯度提升属于人尽皆知的技术。许多数据科学家的工具箱中收录了这一技术，因为它在任何给定的（未知）问题上都能得到很好的结果。

此外，XGBoost是ML竞赛冠军的常用配方。它是如此流行，以至于堆叠XGBoost的想法都成了meme。而且，梯度提升也是许多推荐系统的重要组成部分；有时它甚至成为了品牌。让我们看下梯度提升的历史和发展。

梯度提升源于这样一个问题：能从大量相对弱小、简单的模型得到一个强力模型吗？这里“弱小模型”指的不是决策树这样简单基本的模型，而是精确度表现糟糕的模型，糟糕到比随机猜测好一点的程度。

研究发现，在数学上而言，这一问题的答案是肯定的，但开发实际可用的算法（例如，AdaBoost）花了好几年。这些算法采用了贪婪的做法：首先，通过重新加权输入数据创建简单模型（基本算法）的线性组合；接着，基于之前错误预测的对象（给予更大权重）创建模型（通常是决策树）。

很多机器学习课程讨论了AdaBoost——GBM的祖先。然而，现在看来，AdaBoost不过是GBM的一个特定变体。

这一算法本身定义权重的直觉很清晰，通过可视化的方法很好解读。让我们查看下面的玩具分类问题，我们将在AdaBoost的每次迭代中在深度为1的树间分割数据。

数据点的大小对应其权重，为不正确的预测分配。在每次迭代中，我们看到因为未能正确分类权重增加了。然而，如果我们进行加权投票，就能得到正确的分类：

下面是一个更详细的AdaBoost的例子，我们看到，随着迭代的进行，权重增加了，特别是在分类的边界处。

AdaBoost效果不错，但为何这一算法如此成功却缺乏解释，这正是一些疑惑产生的源头。有些人认为AdaBoost是一个超级算法，一枚银弹，但另一些人顾虑重重，相信AdaBoost只不过是过拟合。

过拟合问题确实存在，特别是当数据具有强离群值时。因此，AdaBoost在这类问题上的表现不稳定。幸运的是，一些斯坦福统计学教授开始研究这一算法（这些教授发明了Lasso、Elastic Net、随机森林）。1999年，Jerome Friedman推广了提升算法——梯度提升（机器），简称GBM。Friedman的这项工作为采用提升优化这个一般方法的许多算法提供了统计学基础。

CART，bootstrap在内的许多算法源自斯坦福统计学部门。这些算法的提出，为他们在未来的教科书中留下了位置。这些算法非常实用，而一些最近的工作尚未广泛普及。例如，glinternet。

网上没有太多Friedman的视频，不过，有一个非常有趣的访谈，关于如何提出CART，以及CART如何解决统计学问题（很像今天的数据分析和数据科学）：https://youtu.be/8hupHmBVvb0 另外推荐Hastie的讲座：https://youtu.be/zBk3PK3g-Fc，我们今天日常使用的很多方法的创造者对数据分析的回顾。

GBM的历史

GBM从提出到成为数据科学工具箱的必备组件花了十多年。GBM的扩展用于不同统计学问题：GBM模型加强版GLMboost、GAMboost，用于存活曲线的CoxBoost，用于排序的RankBoost和LambdaMART。

GBM的许多实现以不同的名字出现在不同的平台上：随机GBM，GBDT（梯度提升决策树），GBRT（梯度提升回归树），MART（多重累加回归树）…… 此外，由于ML社区各自为营，很难追踪梯度提升变得多么普及。

同时，梯度提升大量用于搜索排序。搜索排序问题可以基于惩罚输出顺序误差的损失函数重新表述，从而便于直接插入GBM。AltaVista是第一个在搜索排序中引入梯度提升的公司之一。很快，Yahoo、Yandex、Bing等也采用了这一想法。自此之后，梯度提升不再仅仅用于研究之中，同时成为业界的核心技术之一。

ML竞赛，特别是Kaggle，在梯度提升的流行中起到了主要作用。Kaggle为研究人员提供了一个可以和世纪各地大量参与者一起竞争数学科学问题的公共平台。在Kaggle上，可以在真实数据上测试新算法，这就给了算法“闪耀”的机会。Kaggle提供了模型在不同竞赛数据集上的表现的完整信息。这正是梯度提升用于Kaggle竞赛后所发生的事（自2011年以来，Kaggle冠军的访谈中大多提到自己使用了梯度提升）。XGBoost库出现后迅速流行开来。XGBoost并不是一个新颖独特的算法；它只是经典GBM的一个极其高效的实现（加上了一些启发式算法）。

GBM的经历也是今天许多ML算法的经历：初次出现之后，从数学问题和算法工艺到成功的实践应用和大规模使用花了许多年。

GBM算法

我们将求解一个一般的监督学习设定下的函数逼近问题。特征集记为X，目标变量记为y，我们需要重建y = f(x)这一依赖。我们通过逼近f(x)重建这一依赖，基于损失函数L(y, f)判断哪个逼近较好：

在此阶段，我们对f(x)的种类、逼近模型、目标变量的分布不做任何假定。我们只期望L(y, f)是可微的。最小化数据损失（基于具体数据集的总体均值）的表达式为：

不幸的是，这样的函数不仅数目很多，而且函数空间有着无穷维。因此，需要限制搜索空间至某些函数家族。这大大简化了目标，因为我们现在只需解决参数值的优化问题。

查找最佳参数经常不存在简单的解析解，我们通常迭代地逼近参数。我们在一开始写下经验损失函数，让我们可以基于数据演算参数，并写下M次迭代后的参数逼近之和：

接着，我们只需找到一个合适的最小化上式的迭代算法。梯度下降是最简单、最常用的选项。我们定义损失函数在当前逼近上的梯度，然后在迭代演算中减去梯度。最终我们只需初始化第一次逼近，并选择迭代次数M。

函数梯度下降

让我们想象一下，我们可以在函数空间中进行优化，迭代搜索函数逼近本身。我们将逼近表述为增量改进之和，每个改进都是一个函数。

目前为止没有实际发生什么事；我们只是决定并不以具有大量参数的巨大模型（例如，神经网络）的方式搜索逼近，而是以函数之和的方式搜索逼近，假想我们在函数空间中移动。

为了完成这一任务，我们需要限制搜索空间至某个函数家族：

在迭代的每一步，我们需要选择最优参数ρ ∈ ℝ。第t步需要求解的问题如下：

这是关键之处。我们以一般形式定义了所有的目标，假装我们可以为任意种类的损失函数L(y, f(x, θ))定义任意种类的模型h(x, θ)。在实践中，这极为困难。幸运的是，有一种简单方法可以解决这一任务。

一旦我们知道了损失函数的梯度表达式，我们就可以在数据上计算相应的值。这样，我们可以训练模型，使其预测和梯度（取反）更相关。换句话说，我们将基于预测和这些残差的最小平方差纠正预测。因此，第t步最终转化为以下问题：

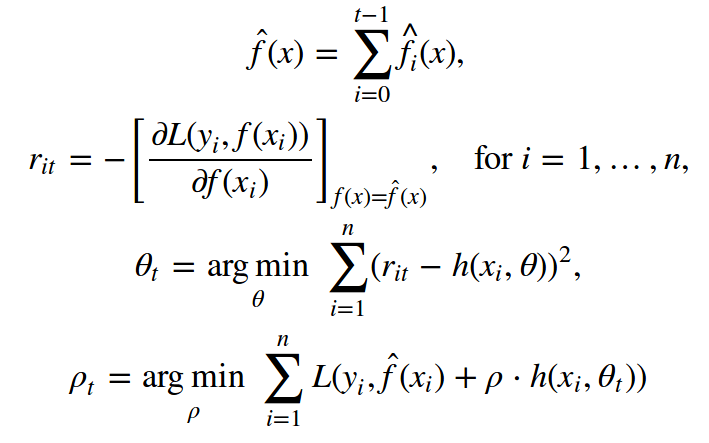
Friedman的经典GBM算法

下面我们讲下Jerome Friedman在1999年提出的经典GBM算法。它是一个具备以下要素的监督算法：

数据集{(xi, yi)}i=1,…,n

迭代数M

梯度定义良好的损失函数L(y, f)

基础算法对应的函数家族h(x, θ)及其训练过程

h(x, θ)的其他超参数（例如，决策树的深度）

还剩下初次逼近f0(x)没讲。出于简单性，初次逼近使用一个常数γ。这个常数值γ和最优参数ρ，均通过二元搜索或其他基于初始损失函数（非梯度）的线搜索算法得出。

GBM算法过程如下：

使用常数值初始化GBM：

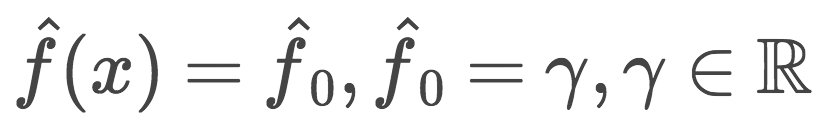
每次迭代t = 1, …, M，重复以上逼近过程；

在i = 1, …, n上计算伪残差rt：

以伪残差{(xi, rit)}i=1,…,n上的回归作为基础算法ht(x)

据ht(x)的初始损失函数找出最优参数ρt：

保存

更新当前逼近：

组成最终GBM模型：

征服Kaggle和全世界

GBM如何工作

让我们通过一个例子演示下GBM是如何工作的。在这个玩具示例中，我们需要重建以下函数：

这是一个实数值的回归问题，所以我们将选择均方误差损失函数。我们将生成300对观测，然后通过深度为2的决策树逼近它们。罗列下使用GBM所需的要素：

玩具数据 {(xi, yi)}i=1,…,300 ✓

迭代数 M = 3 ✓

均方误差损失函数 L(y,f) = (y-f)2 ✓

L(y,f)（L2损失）的梯度不过是残差r = (y-f) ✓

基础算法h(x)为决策树 ✓

决策树的超参数：树深等于2 ✓

就均方误差而言，γ和ρt的初始化很简单。我们初始化GBM时将所有参数ρt设为1，γ据下式确定：

我们运行GBM然后绘制两种图形：当前逼近（蓝色）和在伪残差上构建的每棵树（绿色）。

从上图我们可以看到，我们的决策树在第二次迭代时恢复了函数的基本形式。然而，第一次迭代时算法只创建了函数的“最左部分”（x ∈ [-5, -4]）。这是因为我们的决策树不具备足够的深度一下子创建对称分支，所以它首先关注误差较大的最左部分。

剩下的过程不出我们的意料——每一步的伪残差下降了，随着迭代的进行，GBM越来越好地逼近原函数。然而，决策树的构造决定了它无法逼近一个连续函数，这意味着在这个例子中GBM的效果不是很理想。如果你想以可视化的方式试验GBM函数逼近，可以使用Brilliantly wrong提供的工具：http://arogozhnikov.github.io/2016/06/24/gradient_boosting_explained.html

损失函数

如果我们想要求解一个分类问题，而不是回归问题，那需要做什么变动？只需选择一个合适的损失函数L(y,f)。正是这一最重要的高层的契机，决定了我们将如何优化，以及我们期望最终的模型将具有哪些特性。

我们并不需要自行发明这些——研究人员已经替我们做了。现在我们将探索用于最常见的两种目标的损失函数：回归和二元分类。

回归损失函数

最常用的选项为：

L(y,f) = (y-f)2，即L2损失或高斯损失。这一经典的条件平均数是最简单也是最常见的情形。如果我们不具备额外信息，也不要求模型的鲁棒性，那么可以使用高斯损失。

L(y,f) = |y-f|，即L1损失或拉普拉斯损失。事实上它定义了条件中位数。如我们所知，中位数对离群值的鲁棒性更好，所以这一损失函数在某些情形下表现更好。对大偏差的惩罚不像L2那么大。

Lq损失或分位数损失：

其中α ∈ (0,1). Lq使用分位数而不是中位数，例如，α = 0.75. 如下图所示，这一函数是不对称的，对定义的分位数右侧的观测惩罚力度更大。

让我们试验下Lq的效果。目标是恢复余弦的条件75%分位数。列出GBM所需要素：

玩具数据 {(xi, yi)}i=1,…,300 ✓

迭代数 M = 3 ✓

损失函数 L0.75(y,f) ✓

L0.75(y,f)的梯度 ✓

基础算法h(x)为决策树 ✓

决策树的超参数：树深等于2 ✓

初次逼近将使用所需的y的分位，但我们并不知道最佳参数该取什么值，所以我们将使用标准的线搜索。

结果等价于L2损失加上约0.135的偏置。但是如果我们使用的是90%分位数的话，那我们就不会有足够的数据了（失衡分类）。当我们处理非标准问题时，需要记住这一点。

人们为回归任务开发了许多损失函数。例如，Huber损失函数，离群值较少时，和L2类似，但超出定义的阈值后，转变为L1，从而降低离群值的影响。

下面是一个例子，数据生成自函数y = sin(x) / x，加上噪声（正态分布和伯努利分布的混合分布）。

在这个例子中，我们使用样条作为基础算法。你看，梯度提升并不总是需要使用决策树的。

上图很清楚地显示了L2、L1、Huber损失的区别。如果我们为Huber损失选择最优的参数，可以得到最佳的逼近。

不幸的是，流行的库/软件包中，只有很少支持Huber损失；h2o支持，XGBoost不支持。Huber损失和条件expectiles有关——相对而言更奇异，但仍然值得了解的知识。

分类损失函数

现在让我们看下二元分类问题。技术上说，我们有可能基于L2回归解决这一问题，但这不是正规做法。

目标变量的分布（y ∈ {−1,1}）需要我们使用对数似然，所以我们需要不同的损失函数。最常见的选择为：

L(y,f) = log(1 + exp(−2yf))，即逻辑损失或伯努利损失。这个损失函数有一个有趣的性质，它甚至会惩罚正确预测的分类——不仅优化损失，同时使分类分得更开。

L(y,f) = exp(-yf)，即AdaBoost损失。使用该损失函数的AdaBoost等价于GBM。从概念上讲，这个函数和逻辑损失很相似，但对错误预测有更重的指数惩罚。

让我们生成新的分类问题的玩具数据。我们将使用前面提到的加噪余弦作为基础，并使用符号函数得到目标变量的分类。我们的玩具数据如下图所示（加入了抖动噪声）：

我们将使用逻辑损失。让我们再一次罗列GBM的要素：

玩具数据 {(xi, yi)}i=1,…,300, y ∈ {−1,1} ✓

迭代数 M = 3 ✓

损失函数为逻辑损失，梯度计算方法见下 ✓

基础算法h(x)为决策树 ✓

决策树的超参数：树深等于2 ✓

逻辑损失梯度计算

这次，算法的初始化要困难一点。首先，我们的分类并不均衡（63%对37%）。其次，损失函数的初始化没有已知的解析公式，所以我们需要通过搜索解决：

我们的最优初始逼近在-0.273左右。你可能猜想过它应该是负值，因为预测所有项为最流行的分类是最有利的，但没有求出精确值的公式。现在我们终于可以开始GBM过程了：

算法成功恢复了分类的分隔。你可以看到“低部”是如何分开的，因为决策树对负分类（-1）的正确预测更有信心，也可以看到模型如何拟合混合分类。很明显，我们得到了大量正确分类的观测，一些误差较大的观测则是数据中的噪声所致。

权重

有时候，我们会碰到想要使用更特定的损失函数的情形。例如，在财经时序数据上，我们可能需要给时序中的大变动更大的权重；在离网率预测问题中，预测高LTV（客户未来会带来多少利润）的客户的离网率更有用。

统计学战士可能想要自己发明损失函数，写下它的梯度（包括海森矩阵），并仔细检查这一函数是否满足需要具备的性质。然而，有很大的几率会在某处犯下错误，导致计算困难，花费过量时间排错。

有鉴于此，人们提出了一种非常简单的做法（实践中很少有人记得）：使用权重分配函数加权观测。最简单的一个例子是为了平衡分类加上的权重。一般来说，如果我们知道数据的某个子集（输入变量和目标变量）对我们的模型更重要，那么我们可以直接给它们分配较大的权重w(x, y)。

权重需满足以下条件：

权重能够显著降低花在为当前任务调整损失函数上的时间，并鼓励你试验目标模型的性质。权重分配可以充分发挥你的创造性。比如，简单地加上标量权重：

对任意权重而言，我们未必知道模型的统计学性质。将权重与y值相联系经常会变得太复杂。例如，使用正比于|y|的权重在L1损失和L2损失中是不等价的（梯度不考虑预测值本身）。

现在，为我们的玩具数据创建一些非常奇异的权重。我们将定义一个强力的非对称加权函数：

基于这样的权重，我们期望得到两个属性：X的负值细节更少，形成类似初始余弦的函数。我们采用了上一个例子中的GBM，加以调整，最终得到：

我们取得了意料之中的结果。首先，我们可以看到，第一次迭代上的伪残差有着很大的差距，看起来几乎是原本的余弦函数。其次，函数左半部分的图形常常被忽略，函数更偏向具有更大权重的有半部分。第三，第3次迭代得到的函数看起来和原本的余弦函数类似（同时开始稍微有点过拟合了）。

权重是一个高风险的强力工具，可用于控制模型的性质。如果你打算优化损失函数，值得首先尝试下给观测加上权重这一更简单的问题。

结语

今天，我们学习了梯度提升背后的理论。GBM不是一个特定的算法，而是创建模型集成的一种常见方法。这一方法具有足够的灵活性和扩展性——可以训练大量模型，使用不同的损失函数和加权函数。

实际项目和ML竞赛表明，在标准问题上（图像、音频、非常稀疏的数据除外），GBM经常是最有效的算法（更别说在堆叠和高层集成中，GBM几乎总是其中的一部分）。同时，强化学习中GBM也用得不少（Minecraft, ICML 2016）。顺便提下，计算机视觉领域，现在还使用基于AdaBoost的维奥拉-琼斯算法。

在这篇文章中，我们有意省略了关于GBM的正则化、随机性、超参数的问题。我们一直使用很小的迭代数M = 3并非出于偶然。如果我们使用30棵树训练GBM的话，结果的预测性不会那么好：

良好的拟合

过拟合

图片来源： arogozhnikov.github.io