基于由神经网络架构建立的Gram矩阵的特定结构

深度学习的网络训练损失问题一直是学术界关注的热点。过去，利用梯度下降法找到的一般都是局部最优解。近日，CMU、MIT和北京大学的研究人员分别对深度全连接前馈神经网络、ResNet和卷积ResNet进行了分析，并表明利用梯度下降可以找到全局最小值，在多项式时间内实现零训练损失。

在目标函数非凸的情况下，梯度下降在训练深度神经网络中也能够找到全局最小值。本文证明，对于具有残差连接的超参数化的深度神经网络（ResNet），采用梯度下降可以在多项式时间内实现零训练损失。

本文的分析基于由神经网络架构建立的Gram矩阵的特定结构。该结构显示在整个训练过程中，Gram矩阵是稳定的，并且这种稳定性意味着梯度下降算法的全局最优性。使用ResNet可以获得相对于全连接的前馈网络架构的优势。

对于前馈神经网络，边界要求每层网络中的神经元数量随网络深度的增加呈指数级增长。对于ResNet，只要求每层的神经元数量随着网络深度的实现多项式缩放。我们进一步将此类分析扩展到深度残余卷积神经网络上，并获得了类似的收敛结果。

找到梯度下降全局最优解，实现训练零损失

深度学习中的一个难题是随机初始化的一阶方法，即使目标函数是非凸的，梯度下降也会实现零训练损失。一般认为过参数化是这种现象的主要原因，因为只有当神经网络具有足够大的容量时，该神经网络才有可能适合所有训练数据。在实践中，许多神经网络架构呈现高度的过参数化。

训练深度神经网络的第二个神秘现象是“越深层的网络越难训练”。为了解决这个问题，采用提出了深度残差网络（ResNet）架构，该架构使得随机初始化的一阶方法能够训练具有更多层数的数量级的神经网络。

从理论上讲，线性网络中的残余链路可以防止大的零邻域中的梯度消失，但对于具有非线性激活的神经网络，使用残差连接的优势还不是很清楚。

本文揭开了这两个现象的神秘面纱。我们考虑设置n个数据点，神经网络有H层，宽度为m。然后考虑最小二乘损失，假设激活函数是Lipschitz和平滑的。这个假设适用于许多激活函数，包括soft-plus。

论文链接： 

https://arxiv.org/pdf/1811.03804.pdf

首先考虑全连接前馈神经网络，在神经元数量m=Ω（poly（n）2O（H））的情况下，随机初始化的梯度下降会以线性速度收敛至零训练损失。

接下来考虑ResNet架构。只要神经元数量m =Ω（poly（n，H）），那么随机初始化的梯度下降会以线性速率收敛到零训练损失。与第一个结果相比，ResNet对网络层数的依赖性呈指数级上升。这证明了使用残差连接的优势。

最后，用相同的技术来分析卷积ResNet。结果表明，如果m = poly（n，p，H），其中p是patch数量，则随机初始化的梯度下降也可以实现零训练损失。

本文的研究证据建立在先前关于两层神经网络梯度下降的研究理念之上。首先，作者分析了预测的动力学情况，其收敛性由神经网络结构引出的Gram矩阵的最小特征值确定，为了降低其最小特征值的下限，从初始化阶段限制每个权重矩阵的距离就可以了。

其次，作者使用Li和Liang[2018]的观察结果，如果神经网络是过参数化的，那么每个权重矩阵都接近其初始化状态。本文在分析深度神经网络时，需要构建更多深度神经网络的架构属性和新技术。

本文附录中给出了详细的数学证明过程

接下来，论文分别给出了全连接前馈神经网络、ResNet和卷积ResNet的分析过程，并在长达20余页的附录部分（本文含附录共计45页）给出了详细的数学证明过程，对自己的数学功底有自信的读者可以自行参看论文。这里仅就ResNet分析过程中，Gram矩阵的构建和研究假设做简要说明。

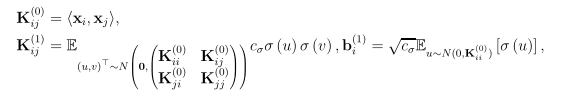
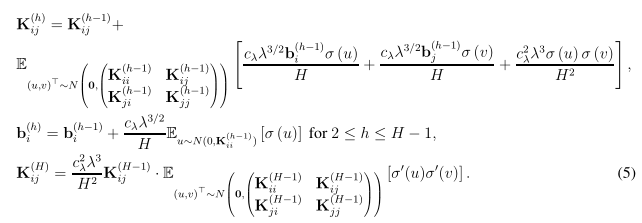
Gram矩阵的构建

以上是网络宽度m趋于无限时的渐进Gram矩阵。我们特做出如下假设，该假设条件决定了收敛速度和过参数化数量。

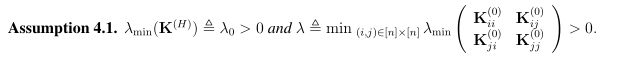
注意，这里的λ和全连接前馈神经网络中的不同，因为这里的λ只由K（0）决定，一般来说，除非两个数据点是平行的，否则λ总是正数。

研究结论和局限：目前还不是随机梯度下降

在本文中，我们表明深度过度参数化网络上的梯度下降可以获得零训练损失。其中关键是证明了Gram矩阵在过参数化条件下会越来越稳定，因此梯度下降的每一步都以几何速率减少损失。

最后列出未来的一些潜在研究方向：

1.本文主要关注训练损失，但没有解决测试损失的问题。如何找到梯度下降的低测试损失的解决方案将是一个重要问题。尤其是现有的成果只表明梯度下降在与kernel方法和随机特征方法相同的情况下才起作用。

2.网络层的宽度m是ResNet架构的所有参数的多项式，但仍然非常大。而在现实网络中，数量较大的是参数的数量，而不是网络层的宽度，数据点数量n是个很大的常量。如何改进分析过程，使其涵盖常用的网络，是一个重要的、有待解决的问题。

3、目前的分析只是梯度下降，不是随机梯度下降。我们认为这一分析可以扩展到随机梯度下降，同时仍然保持线性收敛速度。