

加密货币背后的密码学解析
区块链
描述
你能猜出照片中的这些女人在做什么吗?没错,很难猜。自从1912年发现这份15世纪的手稿以来,一直试图分析破解它。即使是专业的密码专家和历史学家也无法破译它。尽管如此,还是有人提出了一些建议——但所有这些建议都被证明是错误的或毫无根据的。最有根据的猜测要么是基于对其他中世纪手稿中熟悉模式的识别,要么是基于计算最频繁的字母顺序。
后一种方法称为频率分析,它是一种强力搜索,用于解码替代密码(如Caesar密码),这是一种对称加密,通过改变原始消息中的字母位置来形成代码。
如果照片中的两个女人——我们叫她们艾格尼丝和伊莎贝尔——想在别人听不见的情况下彼此分享一个秘密呢?
字母在textIt中的相对频率是一个单字母替换密码,可以简单地用任意预设的字母数量将每个字母沿字母表向下移动。因为它改变了相同字母表的字母,所以通过计算每个字母并找到最常见的一个字母,字母序列是可以破译的。在英语中,很可能是“e”。这是一个典型的英语字母分布。
知道字母“e”在代码中变成了什么,我们可以很容易地计算出其他字母的位置。
一种稍微复杂一点的基于替换的加密方法是多字母密码,它使用混合字母来代替字母。例如,它的一个特殊案例——Vigenere密码——三百年来都无法破译。它使用一个关键字和一个表(tabula recta)对单词进行加密和解密。
一个关键字,也称为移位字,与我们要加密的文本并列。假设阿格尼丝和伊莎贝尔选择了“彩虹”作为转换词。艾格尼丝想告诉伊莎贝尔,她所有的钱都用胶带粘在她的马桶水箱后面。她把“彩虹”这个词抄了很多遍,因为她的文字很长:
现在,要用一个关键字加密这个句子,她需要把表格里的字母替换成原来的字母。行由关键字决定,列由她句子中的字母决定。例如,为了替换“a”,她在“a”列下查找“r”行。下一个字母是“l”,然后是“t”,以此类推。
然而,如果他们的一个朋友——伊娃——截获了一封含有“替换”字的信,这条信息就很容易破译。艾格尼丝和伊莎贝尔显然需要更可靠的东西。
在19世纪,一次性密码垫在加密技术上迈出了新的一步。一次性密码垫使用的原理与之前的密码相似,但使用的不是移位字,而是整个随机字母序列,长度与原始信息一样长。一次性密码垫是密码学上的一个突破,因为它们包含了信息理论之父克劳德•香农(Claude Shannon)所称的完全保密的伪随机性概念。
暴力攻击对一次性密码垫是无能为力的,因为对人类来说,这需要处理太多的选项。例如,对于一个371个字母的消息,有一个371个字母的键,每个字符可以取26个值。因此,可能的键的数量是26 ^ 371年或10 ^ 525。
上个世纪的战争推动了密码学的发展,不仅导致了著名的恩尼格玛计算机的诞生,也激发了新一代的数学加密技术,即非对称密码学。
首先是关于恩尼格玛机器。这些机器的设计是绝对的艺术发展,仍然是基于对称键的原则。但是操作中的人为因素是它们衰败的原因之一。
另一个重要的原因是,一个字母不能像它自己一样加密——它必须是另一个字母。
如今,破解对称加密的解决方案如此之多,以至于你可以在网上进行破解。因此,这些方法都不涉及到保护加密货币钱包。它们受到更强大的非对称加密系统的保护,该系统涉及一对用于加密和解密的公钥和私钥。
简单地说,如果一个神秘的女人想用不对称加密的方式向另一个女人发送消息,她会使用公钥来锁定信息。为了解码消息,她的朋友会使用与她收到的公钥相对应的私钥。然而,这要复杂一些。
Diffie-Hellman算法解决了Enigma机器的问题——现在密钥不需要以物理形式传输(例如在纸上的列表)。
为了在Diffie-Hellman的帮助下交换键,阿格尼丝和伊莎贝尔首先需要在一个基本模量和一个发电机上达成一致。他们同意是17和3。然后阿格尼丝选择她的私人号码,计算发电机(3)的15次方。她可以公开把结果寄给伊莎贝尔。当伊莎贝尔得到它时,她选择了自己随机的私人号码。她用模量17计算出发电机(3)的13次方,并将结果(12)公开发送给阿格尼丝。
这是狡猾的部分。艾格尼丝拿着她收到的结果,将其提升到她的私人号码的幂,以获得秘密信息(10号)。伊莎贝尔得到了阿格尼丝的公开结果,并将其提升到她的私人号码的幂,得到了同样的秘密信息,也就是10号。
他们以不同的顺序对指数进行了同样的计算(都计算了3的私人数字的幂)。如果你交换指数的位置,结果不会改变。
RSA使用公钥和私钥对,其中第一个用于加密,第二个用于解密。这就是为什么它被称为非对称算法。它使用一个活门函数,这是一个单向函数,很容易执行,但很难逆转。换句话说,它是一个数学锁,需要第二个单向函数(或称为陷阱门的特殊信息)来解密消息。
首先,艾格尼丝和伊莎贝尔在两个质数p和q上达成了一致。
然后,根据公式计算得到的通分,并选择指数: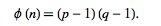
作为Diffie-Hellman算法,RSA使用模块化求幂运算。公钥使用用于加密的模数(n)和指数(e)生成。私钥由用于解密的模(n)和秘密私指数(d)生成。
在计算中使用的整数是素数,这使得解密成为一项费时费力的任务,因为对大素数进行因式分解很困难——这就是所谓的因式分解问题。
这些是密码算法的基本技巧。当然,艾格尼丝和伊莎贝尔l需要成为使用非对称算法的计算机,因为解决质数分解问题需要很高的计算能力。尽管看起来15世纪的神秘女性能够很好地隐藏她们的秘密,以至于今天的密码专家仍在试图破解她们的秘密,但对她们来说,不对称加密技术同样是一种可靠的解决方案。这就是加密货币钱包选择这种方法来保证你资金安全的原因。
-
密码学原理的应用2023-08-02 627
-
基础密码学的概念介绍2022-08-10 2078
-
物联网安全机制密码学基础2021-07-22 2311
-
密码学货币钱包的发展方向分析2020-02-22 1211
-
椭圆曲线密码学详细解析2020-01-06 8160
-
比特币的密码学基础详细解析2019-12-15 9963
-
如何理解区块链密码学中的非对称加密2019-11-29 2651
-
未来密码学货币将呈现出三个方面的走势2019-06-03 1004
-
应用密码学的资料概述2019-04-04 1313
-
加密货币与法币并不是竞争而是共存的关系2018-11-30 1523
-
区块链的底层技术是密码学2018-11-22 2339
-
加密货币怎么赚钱2018-01-15 5660
-
现代密码学2013-05-10 1838
-
密码学中的加密技术2009-06-16 836
全部0条评论

快来发表一下你的评论吧 !

