支持向量机的分类思想

前言

支持向量机是一种经典的机器学习算法，在小样本数据集的情况下有非常广的应用，我觉得，不懂支持向量机不算是入门机器学习。本篇循序渐进的讲解了支持向量机的分类思想，希望对您有帮助。

目录

1.  函数间隔和几何间隔

2.  支持向量机的分类思想

3.  总结

1. 函数间隔和几何间隔

为了能够更好的阐述支持向量机的分类思想，需要理解函数间隔和几何间隔的定义。

1. 点到超平面的距离

假设超平面方程：

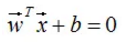
点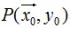到平面的距离：

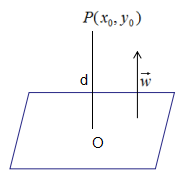
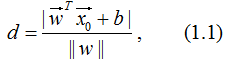
由上式可得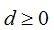：没有分类信息，而函数间隔和几何间隔不仅包含了距离信息，还包含了分类信息。

2. 函数间隔和几何间隔

对于给定的训练数据集T，正样本和负样本分别为+1和-1，我们对式（1.1）稍微进行了修改：

(1).  点到平面的距离不作规范化处理，得：

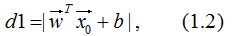
(2).  去掉绝对值符号，并乘以标记结果y0，得：

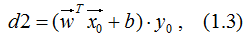
d2表达式就是函数间隔的定义，有两层含义：大小表示点P0到超平面的距离，正负表示点P0是否正确分类，若d<0，分类错误；反之，则分类正确。

因此，我们定义点到超平面的函数间隔为：

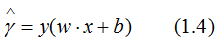
接着定义训练数据集T的函数间隔是所有样本点(xi,yi)的函数间隔的最小值，即：

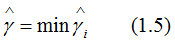
其中，

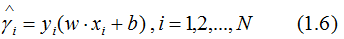
但是，若成比例的增加超平面参数w和b，超平面没有改变，但是函数间隔却成比例的增加了，这是不符合理论的，因此，需要对函数间隔进行规范化，得：

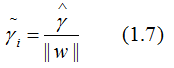
(1.7)式就是几何间隔的定义，几何间隔的值是确定的。

2.  支持向量机的分类思想

1.  感知机和logistic回归的分类思想

感知机的损失函数为所有误分类点到超平面的距离之和：

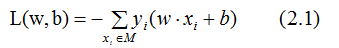
无误分类点时，损失函数为0，满足模型分类条件的超平面有无数个，如下图：

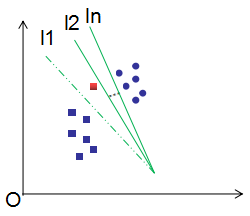
初始超平面为l1，误分类点为红色框，最小化式（2.1）有无穷多个满足损失函数为0的超平面，如上图的l2~ln，然而，最佳分类超平面只有一个，即支持向量机所对应的超平面。

假设logistic回归的模型是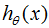，logistic回归的损失函数：

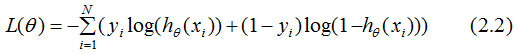
简单分析（2.2）式的分类思想：

(1).  当yi=1时，损失函数简化为：

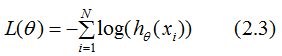
若要使损失函数越小越好，则xi的值越大越好，如下图：

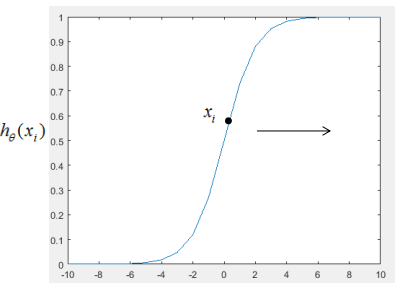
图2.1

当往箭头方向移动时，损失函数逐渐变小。

(2).  当yi=0时，损失函数简化为：

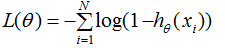
若要使损失函数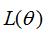越小越好，则xi的值越小越好，如下图：

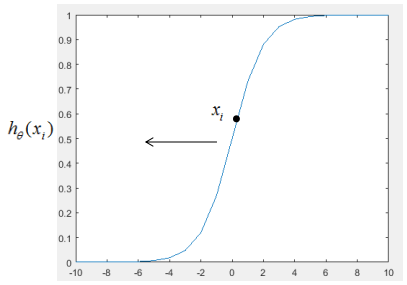
当往箭头方向移动时，损失函数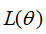逐渐变小。

2. 支持向量机的分类思想

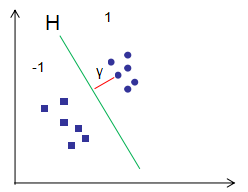
支持向量机结合了感知机和logistic回归分类思想，假设训练样本点(xi,yi)到超平面H的几何间隔为γ(γ>0)，由上节定义可知，几何间隔是点到超平面最短的距离，如下图的红色直线：

用logisitic回归模型分析几何间隔：

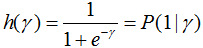
因此，当γ越大时，损失函数越小，结果为正样本的概率也越大。

因此，感知机的分类思想是最大化点到超平面的几何间隔，这个问题可以表示为下面的约束最优化问题：

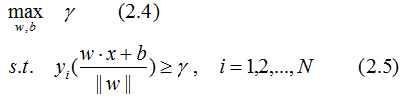
根据几何间隔和函数间隔的关系，得几何间隔的约束最优化问题：

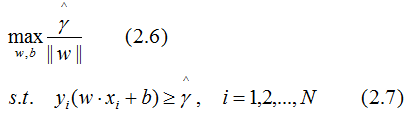
函数间隔是样本点到超平面的最短距离，因此，令函数间隔为常数1，那么其他样本点到超平面的距离都大于1，且最大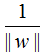化和最小化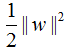是等价的。于是就得到下面的最优化问题：

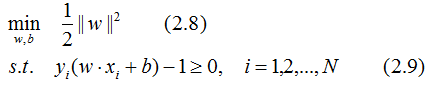
由(2.8)式和(2.9)式，解得最优解w*,b*，易知最优超平面到正负样本的几何间隔相等（请理解几何间隔的含义，然后仔细回想整个分类过程，就会得到这个结论）。

3. 总结

本文结合了感知机和logistic回归的分类思想来推导支持向量机的最优化问题，即最大间隔分离超平面。