

连续时间信号的重建分析概述
描述
今天,来看一看连续时间信号的重建(或者称为信号的恢复)。首先呢,来唠一唠,“重建”或者称为“恢复”是何意?不知道大家如何想的,反正我在当学生学这部分内容时,我的感觉是,好不容易采样了,为啥又去恢复?这不吃饱了撑的吗?
其实呢,我们可以从两方面来理解信号重建的意义:一方面,从理论分析的层面来说,我们可以通过信号的重建,来证明抽取后的离散样值,确实能代表原来连续时间信号的全部信息。第二个,在实际应用的层面,如下图所示,是一般的数字信号处理系统框图,中间的“通用/专用计算机”来完成对数字信号的处理。它的前面(红色框框),需要把模拟信号转换成数字信号,它的后面(黄色框框),又需要把处理后的数字信号,转换为模拟信号。可以说,我们信号与系统中所学的“时域抽样”,对应AD转换的理想模型;而“信号的重建(恢复)”对应DA转换的理想模型。
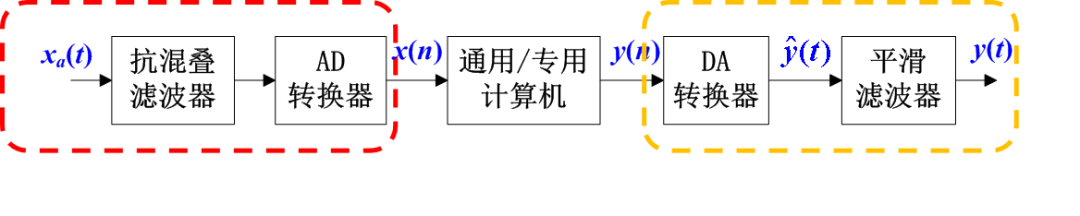
图0
本文不涉及实际数字信号处理中的ADC和DAC,关于这部分内容,感兴趣的同学可以参考本公众号以前发过的文章,链接如下:
数字信号处理中的采样与信号重建
本文主要讨论三种时域采样模型对应的连续时间信号的重建问题。
总体思路:如前文所述,不管哪种模型,采样后信号的频谱,都是原来连续时间信号频谱的周期延拓,在满足采样定理要求的前提下,频域的周期延拓就不会混叠,这样,只要通过合适的低通滤波器,把周期延拓后其他的频谱都滤除,只保留w=0附近的这部分频谱,并且要使得这部分频谱与原来的连续时间信号的频谱完全相同,就可以恢复原始的连续时间信号了。
第一种,理想冲激串采样
连续时间信号的频谱和经过理想冲激串采样后信号的频谱如下图所示。因此,只要把抽样信号通过理想低通滤波器,理想低通滤波器通带的增益为常数T(正好抵消抽样信号频谱周期延拓时的系数1/T),并且理想低通滤波器的截止频率wc正好位于wm和ws-wm之间,也就是使得w=0附近的这部分频谱完全通过,而其他的频谱完全滤除掉,就可以了。
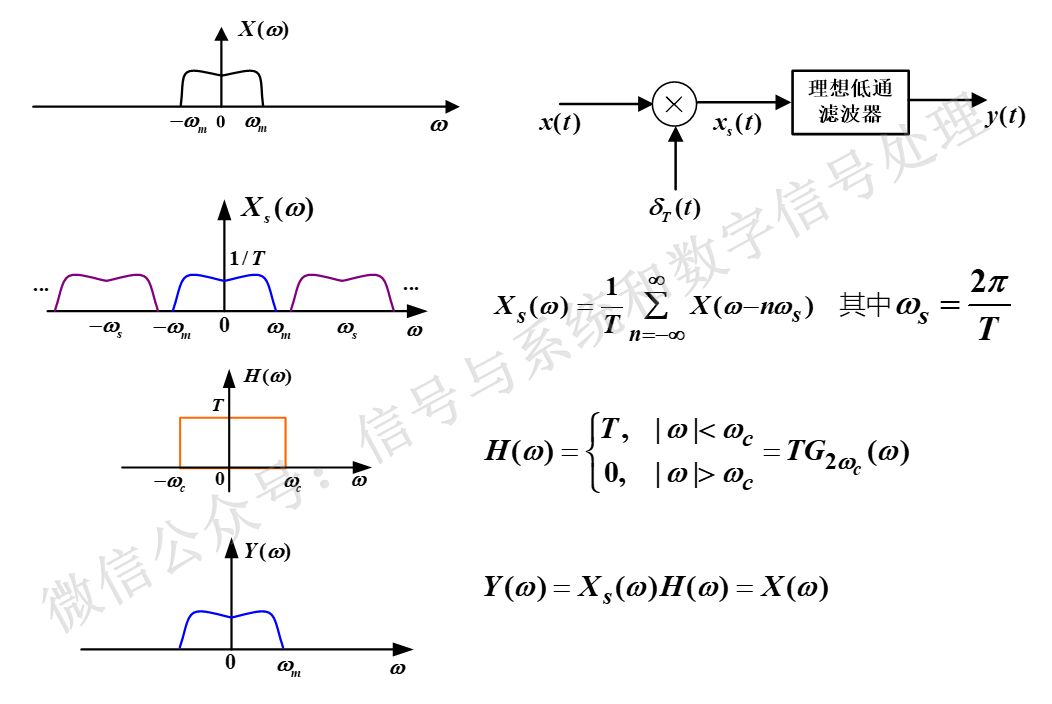
图1
第二种,脉冲串采样(曲顶采样)
如图2所示,看抽样信号的频谱Xs(jw)这个公式,看似复杂,其实不然你,把这个求和形式展开写,发现每个周期延拓的频谱前面乘的这个系数,看上去像个sinc函数,但实际上,仅仅是sinc函数在延拓的这个位置处的取值(是个常数)而已。w=0位置处的这个系数,是τ/T,所以理想低通滤波器的通带增益,只要把这个系数τ/T抵消掉,也就是T/τ,就可以了。这样就很容易得到用于信号重建的理想低通滤波器的频率响应H(jw)的表达式。与图1相比,仅仅是T变成了T/τ而已。
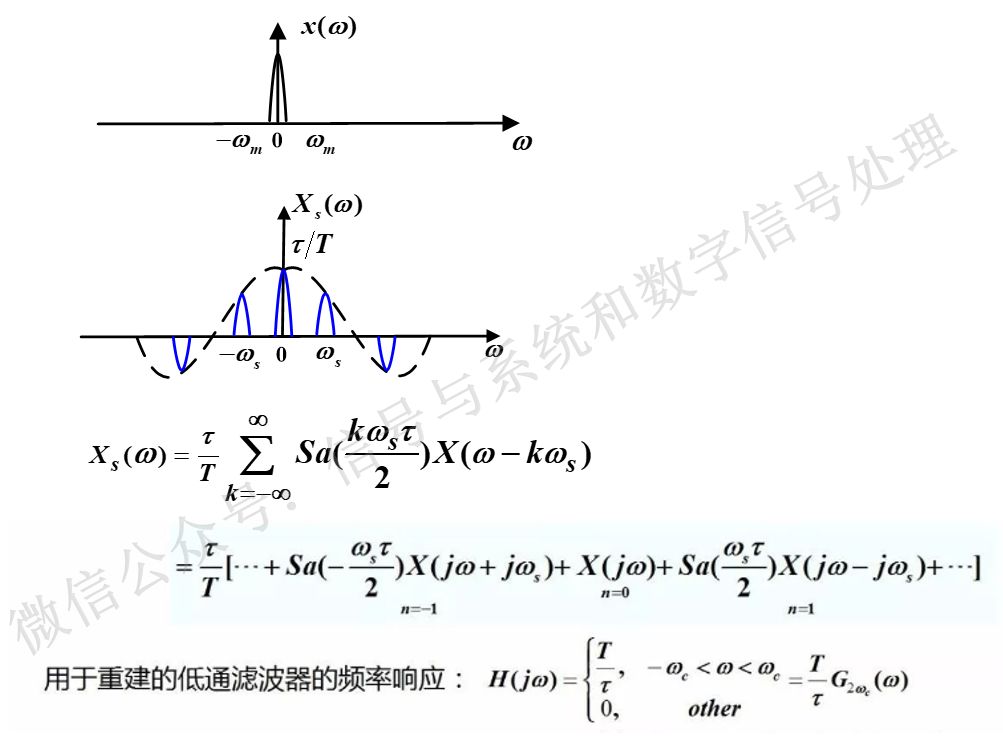
图2
第三种,脉冲串采样(平顶采样)
平顶抽样的情况稍显复杂,用于重建的滤波器,依然是低通滤波器,但它的频率响应函数,就不能再是一个常数,而是要把周期延拓时所乘的sinc函数抵消掉,所以,重建的低通滤波器的通带增益是把sinc函数放在分母上,如图3中的公式所示。
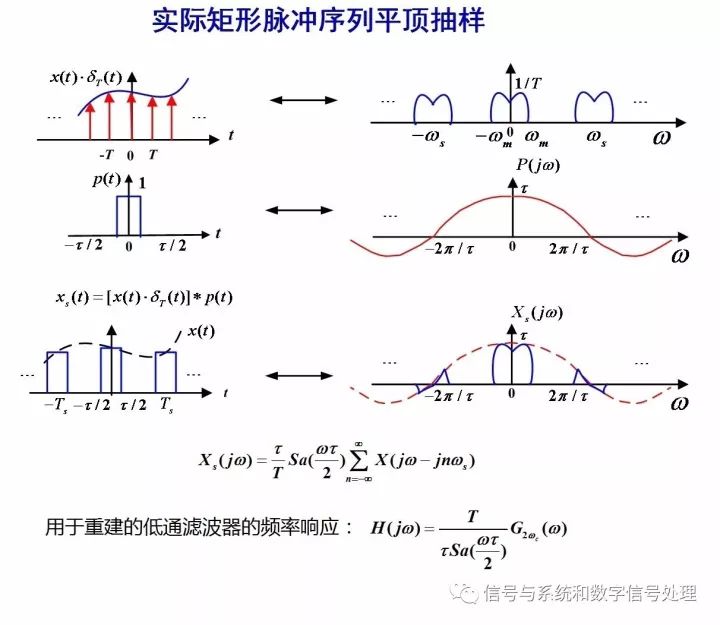
-
连续时间信号的傅里叶分析2023-11-18 423
-
连续时间系统时域分析的MATLAB实现2020-11-10 1236
-
信号与系统教程之连续时间系统的时域分析2018-10-29 1184
-
系统与信号教程之信号的时域分析的资料概述2018-10-17 1447
-
连续信号与系统的时域分析 信号与系统第二章电子课件免费下载2018-08-23 1297
-
连续时间信号频域周期信号傅里叶级数和非周期信号傅里叶变换的分析2018-05-19 59784
-
连续信号频谱分析工具使用及原理2017-10-23 11750
-
连续时间信号的Matlab表示与计算实验2016-12-17 741
-
§2连续时间系统的时域分析2016-05-09 693
-
从抽样信号恢复连续时间信号2010-05-27 851
-
连续时间系统的时域分析2009-10-04 1063
-
连续时间LTI系统的频域分析2009-09-16 1078
-
连续时间信号与系统的傅立叶分析2009-08-26 870
-
离散时间信号分析和处理2008-10-02 2387
全部0条评论

快来发表一下你的评论吧 !

