如何在Python中划分训练/测试集并进行交叉验证

编者按：训练集/测试集划分和交叉验证一直是数据科学和数据分析中的两个相当重要的概念，它们也是防止模型过拟合的常用工具。为了更好地掌握它们，在这篇文章中，我们会以统计模型为例，先从理论角度简要介绍相关术语，然后给出一个Python实现的案例。

什么是模型过拟合/欠拟合

在统计学和机器学习中，通常我们会把数据分成两个子集：训练数据和测试数据（有时也分为训练、验证、测试三个），然后用训练集训练模型，用测试集检验模型的学习效果。但当我们这么做时，模型可能会出现以下两种情况：一是模型过度拟合数据，二是模型不能很好地拟合数据。常言道过犹不及，这两种情况都是我们要极力规避的，因为它们会影响模型的预测性能——预测准确率较低，或是泛化性太差，没法把学到的经验推广到其他数据上（也就是没法预测其他数据）。

过拟合

模型过拟合意味着我们把模型“训练得太好了”，通过一遍又一遍的训练，它已经把训练数据的特征都“死记硬背”了下来。这在模型过于复杂（和观察样本数相比，模型设置的特征/变量太多）时往往更容易发生。过拟合的缺点是模型只对训练数据非常准确，但在未经训练的数据或全新数据上非常不准确，因为它不是泛化的，没法推广结果，对其他数据作出任何推断。

更确切地说，过拟合的模型学习到的只是训练数据中的“噪声”，而不是数据中变量之间的实际关系。显然，这些“噪声”是训练数据独有的，这也决定了它不能准确预测任何新数据集。

欠拟合

和过拟合相比，欠拟合是另一个极端，它意味着模型连拟合训练数据都做不到，没能真正把握数据的趋势。毫无疑问，一个欠拟合的模型也是不能被推广到新数据的，它和过拟合恰恰相反，是模型过于简单（没有足够的预测变量/自变量）的结果。例如，当我们用线性模型（比如线性回归）拟合非线性数据时，模型就很可能会欠拟合。

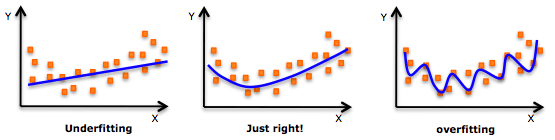
欠拟合、恰到好处和过拟合

值得注意的是，在实践中，欠拟合远不像过拟合那么普遍。但我们还是要做到在数据分析中同时警惕这两个问题，找到它们的中间地带。而解决问题的首选方案就是划分训练/测试数据和交叉验证。

划分训练/测试数据

正如之前提到的，我们使用的数据通常会被划分为训练集和测试集。其中训练集包含输入的对应已知输出，通过在上面进行训练，模型可以把学到的特征关系推广到其他数据上，而测试集就是模型性能的试金石。

那么在Python中，我们能怎么执行这个操作呢？这里我们介绍一种用Scikit-Learn库，特别是traintestsplit的方法。让我们先从导入库开始：

import pandas as pd

from sklearn import datasets, linear_model

from sklearn.model_selection import train_test_split

from matplotlib import pyplot as plt

在上述代码中：

第一行作用是把数据导入到pandas数据框架中，然后再进行分析；

第二行表示既然已经导入了数据集模块，所以我们可以加载一个样本数据集和linear_model来做线性回归；

第三行表示已经导入了traintestsplit，所以可以把数据集分成训练集和测试集；

第四行意味着导入pyplot以绘制数据图。

下面我们以糖尿病数据集为例，从实践中看看怎么把它导入数据框架，并定义各列的名称。

数据集地址：scikit-learn.org/stable/modules/generated/sklearn.datasets.load_diabetes.html

# Load the Diabetes Housing dataset

columns =“age sex bmi map tc ldl hdl tch ltg glu”.split()# Declare the columns names

diabetes = datasets.load_diabetes()# Call the diabetes dataset from sklearn

df = pd.DataFrame(diabetes.data, columns=columns)# load the dataset as a pandas data frame

y = diabetes.target # define the target variable (dependent variable) as y

现在我们可以用traintestsplit函数划分数据集。test_size = 0.2表示测试数据在数据集中的占比，一般情况下，训练集和测试集的比例应该是80/20或70/30。

# create training and testing vars

X_train, X_test, y_train, y_test = train_test_split(df, y, test_size=0.2)

print X_train.shape, y_train.shape

print X_test.shape, y_test.shape

(353,10)(353,)

(89,10)(89,)

将模型拟合到训练数据上：

# fit a model

lm = linear_model.LinearRegression()

model = lm.fit(X_train, y_train)

predictions = lm.predict(X_test)

把模型放到测试数据上：

predictions[0:5]

array([205.68012533,   64.58785513,175.12880278,169.95993301,

128.92035866])

注：预测后面那个[0:5]表示只显示前五个预测值，如果把它删掉，模型会输出所有预测值。

然后是绘制模型结果：

## The line / model

plt.scatter(y_test, predictions)

plt.xlabel(“TrueValues”)

plt.ylabel(“Predictions”)

最后输出模型准确度分数：

print“Score:”, model.score(X_test, y_test)

Score:0.485829586737

到这里，划分训练集/测试集就完成了，如果总结整个过程，它可以被概括为先加载数据，将其分成训练集和测试集，用回归模型拟合训练数据，基于训练数据进行预测并在测试集上预测测试数据的结果。一切都好像很完美吧？其实不然，划分数据集也有很多讲究——如果我们划分时没有做到严格意义上的随机呢？如果数据集本身存在明显偏差，其中大部分数据都来自某省、某个收入水平的员工、某个特定性别的员工或只有特定年龄的人，该怎么办？

即便我们一再避免，模型最后还是会过拟合，而这就是交叉验证可以发挥作用的地方。

交叉验证

为了避免因数据集偏差、划分数据集不当引起模型过拟合，我们可以使用交叉验证，它和划分训练集/测试集非常相似，但适用于数量上更多的子集。它的工作原理是先把数据分成k个子集，并从中挑选k-1个子集，在每个自己上训练模型，最后再用剩下的最后一个子集进行测试。

划分训练集/测试集和交叉验证

交叉验证的方法有很多，这里我们只讨论其中两个：第一个是k-折交叉验证，第二个是Leave One Out交叉验证（LOOCV）。

k-折交叉验证

在k-折交叉验证中，我们将数据分成k个不同的子集（分成k折），并在k-1个子集上分别训练单独模型，最后用第k个子集作为测试数据。

以下是k-折交叉验证的Sklearn文档中的一个简单示例：

from sklearn.model_selection importKFold# import KFold

X = np.array([[1,2],[3,4],[1,2],[3,4]])# create an array

y = np.array([1,2,3,4])# Create another array

kf =KFold(n_splits=2)# Define the split - into 2 folds

kf.get_n_splits(X)# returns the number of splitting iterations in the cross-validator

print(kf)

KFold(n_splits=2, random_state=None, shuffle=False)

它的结果是：

for train_index, test_index in kf.split(X):

print(“TRAIN:”, train_index,“TEST:”, test_index)

X_train, X_test = X[train_index], X[test_index]

y_train, y_test = y[train_index], y[test_index]

('TRAIN:', array([2,3]),'TEST:', array([0,1]))

('TRAIN:', array([0,1]),'TEST:', array([2,3]))

如你所见，这个函数将原始数据拆分为不同的数据子集。

LOOCV

LOOCV（留一验证）是本文要介绍的第二种交叉验证方法，它的思路和k-折交叉验证其实有相似之处，但不同的是，它只从原数据集中抽取一个样本作为测试数据，剩余的全是训练数据，整个过程一直持续到每个样本都被当做一次测试数据，最后再用平均值构建最终的模型。可以想见，这种方法势必会得到大量的训练集（等于样本数），所以它的计算量会很大，更适合被用于小型数据集。

让让我们看一下它在Sklearn里的例子：

from sklearn.model_selection importLeaveOneOut

X = np.array([[1,2],[3,4]])

y = np.array([1,2])

loo =LeaveOneOut()

loo.get_n_splits(X)

for train_index, test_index in loo.split(X):

print("TRAIN:", train_index,"TEST:", test_index)

X_train, X_test = X[train_index], X[test_index]

y_train, y_test = y[train_index], y[test_index]

print(X_train, X_test, y_train, y_test)

它的输出是：

('TRAIN:', array([1]),'TEST:', array([0]))

(array([[3,4]]), array([[1,2]]), array([2]), array([1]))

('TRAIN:', array([0]),'TEST:', array([1]))

(array([[1,2]]), array([[3,4]]), array([1]), array([2]))

那么对于这两种交叉验证方法，我们在实践中该怎么取舍呢？事实上，子集越小、子集数量越多，模型的准确率就越高，但相应的，它的计算量也越多，对内存的要求也越大。因此，如果是非常小的数据集，建议大家还是用LOOCV；如果数据集略大，可以采用k-折，比如k=3是一个比较常用的超参数，当然你也可以视情况选择5、10等。

split函数划分 VS 交叉验证

之前我们演示了用函数划分糖尿病数据集的结果，这里我们尝试对它做交叉验证，看看有什么不同。首先，我们可以用cross_val_predict函数返回测试子集中每个数据点的预测值。

# Necessary imports:

from sklearn.cross_validation import cross_val_score, cross_val_predict

from sklearn import metrics

既然我们已经把数据集分成了测试集和训练集，这里我们再在原有基础上进行交叉验证，看看准确率得分变化：

# Perform 6-fold cross validation

scores = cross_val_score(model, df, y, cv=6)

print“Cross-validated scores:”, scores

Cross-validated scores:[0.4554861   0.461385720.400940840.552207360.439427750.56923406]

得分从0.485提高到了0.569，虽然看起来不是很显著，但不要心急，我们来绘制交叉验证后的图像：

# Make cross validated predictions

predictions = cross_val_predict(model, df, y, cv=6)

plt.scatter(y, predictions)

很明显，这幅图里的数据点比之前的图密集多了，因为我们取cv=6。

从本质上来看，回归模型就是用模型拟合数据，这之中肯定存在误差，而衡量这个误差大小的标尺是拟合优度。在众多标准中，R2是度量拟合优度的一个常用统计量，这里我们计算一下模型的R2得分：

accuracy = metrics.r2_score(y, predictions)

print“Cross-PredictedAccuracy:”, accuracy

Cross-PredictedAccuracy:0.490806583864

以上就是文本想要介绍的全部内容，希望你能从中找到对自己有所帮助的东西！