

如何从这些品类繁多的器件中选择适合自己项目的器件?
电子说
描述
上篇文章我们讲述了ADC和DAC是连接模拟世界和数字世界的桥梁,但桥梁有多种 - 有宽窄之分、快慢之分。同样ADC和DAC也有很多公司提供不同种类的器件,如何从这些品类繁多的器件中选择适合自己项目的器件?由于ADC和DAC的差异性还是比较大的,因此我们今天的文章就针对ADC来看一下:
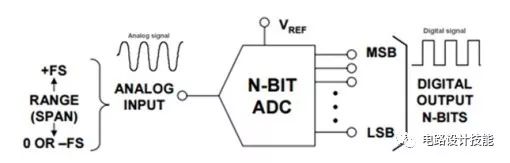
ADC - 将在时间上和幅度上都连续的模拟电信号在一定序列的时钟信号的上升沿或下降沿对其幅度进行量化,生成能够用数字表征的信号幅度值。如下图:

直观上理解,让数字化的信息能够尽可能不失真地表征原来的模拟信号信息,必须具备以下条件(先从静态的信号看):
对信号幅度的量化要足够的精细,也就是要达到一定的细致程度,比如你向一个姑娘介绍对象,说一个身高1.75米的小伙身高一米多、不到两米(只用了10进制中的一个数字),姑娘肯定不满意,即便你说1米7多、不到1米8(用了十进制中的2个数字),她还是不满意,一定要知道他究竟是1.75米还是1.78米。如果你告诉他1.756m,她一定会觉得你吃饱了撑的,因为最后一个数字她并不关心,她也不相信最后一个数字的准确性(1天24小时内会发生变化),因此描述小伙子身高的精度只需要3位数(十进制),少了无法满足系统的要求,多了在这种场景下失去了意义,本身也不准确。
ADC应用中比较直观的就是对声音和图像的量化,就拿图像来比方,如果你用一个bit表征一个像素点,那整个图像就量化后就是黑白的,如果你用4bits来量化每个像素点,可以得到16级灰度的图像,如果你对每个像素点分开三种颜色R、G、B分别以8位进行量化,则就可以得到普通肉眼分辨不出来细节的图像 - 在电脑上屏幕上你能看到一个让你想咬一口的苹果,如果你使用了R、G、B三色都为8位的ADC进行量化的话。
要不要再精细地量化?更精细意味着耗费更多的bit数 - ADC价格增加、存储空间也增加,未必给你的视觉效果带来任何改善,除非某些用户的眼睛对细节的辨别能力超级的强。当然现在的照相机对每个像素点进行采样的分辨率远高于8bit(14bit的ADC很常用),why?这在以后的文章中会讲到,主要是为了得到足够的动态范围,你可以在后期对图像进行亮度、对比度,乃至ISO等等进行调节,省去了ADC前面模拟电路的复杂设计。
结论 - 量化精度的选取,也就是ADC的位数- 分辨率是非常重要的一个指标,我们要根据实际要设计的系统的要求,综合考虑到系统的其它因素以及成本等选定一个合适的位数。记住更多的位数未必给你更精准的信息,因为量化的过程取决于很多因素,量化后产生的误差(error)可能让你后面的位数没有任何意义,比如一个人每天的身高从早上起床到晚上躺下其变化可能在1.75-1.76之间,任何1.75x中国的x都是由于采样时间不同导致的模糊性,也就相当于ADC的量化误差。
想一下 - 量化误差取决于哪些因素?
分辨率- 如果你用1位数,只能说1米多,而1米-2米之间的所有不同都被模糊掉了,如果你用2位,则可以分辨的是1.7或1.8,1.7-1.8之间的所有不同也被模糊掉了,因此由于分辨率不够就会导致量化的误差,看下面的正弦波被不同位数的ADC量化后的数字表征,16bit可以非常精准地描述原来的模拟波形,而3bit的采样则让我们看到像楼梯台阶一样的信号。当然这两个波形的采样时钟频率也不同。
线性度 - 你的量尺理论上应该是刻度均匀的,如果不均匀,用你的标尺测量出来的也就有了误差,这种不均匀就是非线性,我们用的所有ADC都是通过将输入电压同内部的基准电压进行比较来进行判决其所处的区间的,如果每个刻度比较的电路不一致,自然就会造成非线性误差,是电路就会有不一致性,因此非线性的误差一定是存在的,只是不同的工艺、不同的厂商的不同器件其线性度也不同,因此非线性误差也就不同,一般器件会用积分非线性(INL)和差分非线性(DNL)两个指标来进行表征;比如ADI公司的8位ADC器件AD9283在其数据手册中给出的DNL和INL的数据 - 由于非线性导致的误差相当于最小分辨精度(LSB)的值。

供电噪声任何被用来做基准的东西都应该是稳定不变的,比如ADC和DAC中使用的参考电压(内部转换成参考电流),只要是电源供电的电压,就无法100%保证其没有波动(噪声),无论是ADC的模拟电路供电电压,还是参考基准源的电压,都需要尽可能保持干净,其上面的噪声一定会导致量化误差。
时钟边沿抖动(Jitter)- 就如你测量一个人的身高一样,如果被测的人非常规律,你在他每天早上7点起床的时候进行测量,则每次得到的结果都应该是一致的,但如果你有时候6点半测量,有时候是7点半测量,结果会一致么?一定会发生与本该得到的结果有偏差的现象。ADC用周期性时钟进行采样的时候理想状态下每个时钟的时钟沿之间的间隔是固定的,但实际的情况 -由于时钟产生电路的电源噪声、传输途中遭遇的阻抗失配、电磁谐振等,都会导致时钟的相位噪声,也就是时钟的沿发生抖动(学名Jitter),实际的采样点和理论上的采样点发生了偏移,得到的数据自然也就不是本该出现的位置的信息,这种由于时钟相位噪声导致的误差在某种情况下会严重到你使用更高的精度失去了意义,可以想像,越是变化快,变化幅度大的模拟信号由于时钟抖动带来的影响越大,低频信号受到的影响较低,直流信号不受影响。如下表,可以这样解读 - 如果你对10MHz的模拟信号使用10位的ADC进行模数转换,其时钟的边沿抖动不能超过31.1ps;也可以这么讲,如果你采用的时钟信号由于种种原因,只能保证到30ps以内的边沿抖动,你选用超过10位的ADC对模拟带宽为10MHz的信号进行采样是没有意义的,只会浪费钱。


基于以上种种可能导致的误差, 归根结底是你要选用多少位数精度的ADC,很多ADC器件数据手册都会给出ENOB这个指标,也就是该器件在实际的使用中能够保证到的有效的位数(Effective number of bits),

以上是静态信号的量化,但我们处理的信号多数都是幅度随时间发生变化的,根据傅立叶分析,任何一个信号都可以分解为多个不同频率的周期性信号的叠加,这就如同一群人散步,不同的身高,每个人不同的速度(假设每个人的速度是匀速的)。我们将这些不同的频率所处的范围称之为信号占用的频带。要对这些信号进行量化,根据奈奎斯特定律(不知道的自己去查资料进行补习),只要我们的采样频率高于这个模拟信号所占带宽的两倍以上就可以准确表征模拟信号所携带的信息,这就是为什么我们会看到对音频采样有个44.1KHz这么一个奇怪的频率,原因呢?人能听到的音频信号的最高频为20KHz,2倍多一点 - 选择了44.1KHz或48KHz。
这点会让很多人感到费解 - 一个周期的正弦波只用2个以上的点就可以表征?即便是3个点怎么画也感觉出来的波形怪怪的,常规上对一个1MHz的模拟信号采样,怎么也要10Msps吧?用10个点描出一个周期的波形才觉得踏实啊。看下面的图,由于采样频率不够导致采样后的结果跟原来的信号相差十万八千里。
其实在满足了奈奎斯特采样定律之后采集的数据可以在数字域通过各种内插算法恢复出非常漂亮的波形,补齐因每个周期采样点不多导致的波形失真。
针对不同信号采用不同采样频率还有一些概念比如Dithering、Oversampling等技术以提升ENOB,由于篇幅限制在此不专门做介绍,有兴趣的朋友可以自行搜索一些相关的文章来理解一下。
选型的时候在性能方面除了我们要对ADC的采样精度(bits)、最高能支持的转换率(sps)格外关注外,也要看其数据手册中具体使用场景下给出的一些性能参数,比如INL、DNL、ENOB等等。
另外模拟信号的接口方式、数据的接口方式、供电电压、是否内置参考电压源、功耗、价格等都是我们在具体的项目中要综合考虑的要素。
-
初学者如何从这众多的PCB设计工具中选择一款适合自己的2012-08-30 3439
-
EMC器件如何选择2019-05-31 1769
-
怎么选择FPGA器件到我的项目?2020-03-13 1526
-
在KEIL中选择创建HEX文件Crystal Frequency2021-08-04 1161
-
EMC器件选择及电路设计2011-03-29 2232
-
基于inDrop系统的个性化开发,为未来研究中合理选择检测平台提供了数据支持2018-11-26 6756
-
如何选择8位、16位、32位MCU中合适的器件2019-08-23 3687
-
电路过压保护器件有哪些?在选型方面有什么要求2019-07-24 6677
-
如何选择适合自己的开源RTOS2020-03-12 3488
-
电子元器件选择的原则是什么2021-02-12 6256
-
面对种类繁多的UV胶水如何选择2021-11-10 3375
-
如何选择适合自己的连接器2021-04-07 2245
-
如何挑选适合自己项目的工业显示器2023-08-15 1075
-
怎样选择适合自己的点焊机2024-10-15 1964
-
如何选择适合自己项目的通信协议评估工具?2025-08-27 484
全部0条评论

快来发表一下你的评论吧 !

