如何在声音频谱嵌入中加入记忆机制

编者按：Kanda机器学习工程师Daniel Rothmann撰写的机器听觉系列第四篇，讲解如何在声音频谱嵌入中加入记忆机制。

欢迎回来！这一系列文章将详细介绍奥胡斯大学和智能扬声器生产商Dynaudio A/S合作开发的实时音频信号处理框架。

如果你错过了之前的文章，可以点击下面的链接查看：

AI在音频处理上的潜力

基于频谱图和CNN处理音频有何问题？

基于自编码器学习声音嵌入表示

在上一篇文章中，我们介绍了人类是如何体验声音的，在耳蜗形成频谱印象，接着由脑干核团“编码”，并借鉴其思路，基于自编码器学习声音频谱嵌入。在这篇文章中，我们将探索如何构建用来理解声音的人工神经网络，并在频谱声音嵌入生成中集成记忆。

余音记忆

声音事件的含义，很大程度上源于频谱特征间的时域相互关系。

有一个事实可以作为例证，取决于语音的时域上下文的不同，人类听觉系统会以不同方式编码同样的音位1。这意味着，取决于之前的语音，音位/e/在神经方面可能意味着完全不同的东西。

进行声音分析时，记忆很关键。因为只有在某处实际存储了之前的印象，才可能将之前的印象与“此刻”的印象相比较。

人类的短期记忆组件既包括感官记忆也包括工作记忆2。人类对声音的感知依靠听觉感官记忆（有时称为余音记忆）。C. Alain等将听觉感官记忆描述为“听觉感知的关键初始阶段，使听者可以整合传入的听觉信息和存储的之前的听觉事件的表示”2。

从计算的角度出发，我们可以将余音记忆视作即刻听觉印象的短期缓冲区。

余音记忆的持续时间有所争议。D. Massaro基于纯音和语音元音掩码的研究主张持续时间约为250毫秒，而A. Treisman则根据双耳分听试验主张持续时间约为4秒3。从在神经网络中借鉴余音记忆思路的角度出发，我们不必纠结感官存储的余音记忆的固定时长。我们可以在神经网络上测试几秒钟范围内的记忆的效果。

进入循环

在数字化频谱表示中可以相当直截了当地实现感官记忆。我们可以简单地分配一个环形缓冲区用来储存之前时步的频谱，储存频谱的数量预先定义。

环形缓冲区是一种数据结构，其中包含一个视作环形的数组，穷尽数组长度后索引循环往复为04.

在我们的例子中，可以使用一个长度由所需记忆量决定的多维数组，环形缓冲区的每个索引指向某一特定时步的完整频率频谱。计算出新频谱后，将其写入缓冲区，如果缓冲区已满，就覆盖最旧的时步。

在填充缓冲区的过程中，我们会更新两个指针：标记最新加入元素的尾指针，和标记最旧元素的头指针（即缓冲区的开始）4。

下面是一个环形缓冲区的Python实现的例子（作者为Eric Wieser）：

class CircularBuffer():    # 初始化NumPy数组和头/尾指针    def __init__(self, capacity, dtype=float):        self._buffer = np.zeros(capacity, dtype)        self._head_index = 0        self._tail_index = 0        self._capacity = capacity    # 确保头指针和尾指针循环往复    def fix_indices(self):        if self._head_index >= self._capacity:            self._head_index -= self._capacity            self._tail_index -= self._capacity        elif self._head_index < 0:            self._head_index += self._capacity            self._tail_index += self._capacity    # 在缓冲区中插入新值，如缓冲区已满，覆盖旧值    def insert(self, value):        if self.is_full():            self._head_index += 1        self._buffer[self._tail_index % self._capacity] = value        self._tail_index += 1        self.fix_indices()

降低输入尺寸

为了存储一整秒的频率频谱（每时步5毫秒），我们需要一个包含200个元素的缓冲区，其中每个元素包含频率幅度的数组。如果我们需要类人的频谱解析度，这些数组将包含3500个值。然后200个时步就需要处理700000个值。

将长度为700000的输入传给人工神经网络，在算力上太昂贵了。降低频谱和时域解析度，或者保存更短时期的频谱信息，可以缓解这一问题。

我们也可以借鉴Wavenet架构，使用空洞因果卷积（dilated causal convolutions）以优化原始音频样本中的大量序列数据的分析。如A. Van Den Oord等所言，空洞卷积是应用于大于自身长度的区域，以特定步骤跳过输入值的过滤器5。

最近传入的频率数据在瞬时声音分析中起决定性作用，根据这一假定，我们可以用空洞频谱缓冲区来降低算力记忆的大小。

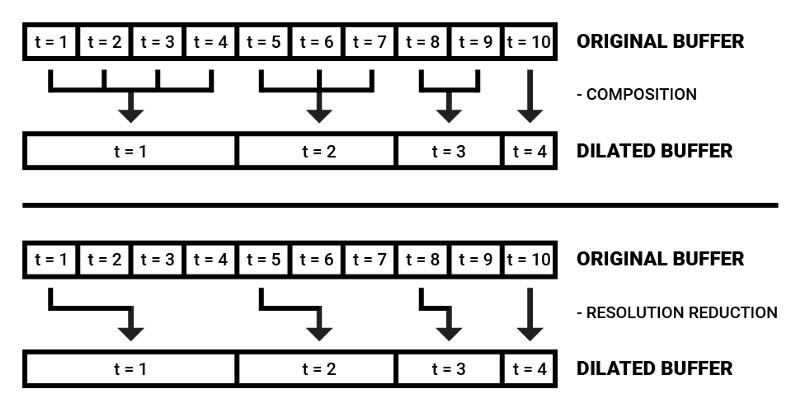
空洞缓冲区的值可以直接选择单个值，也可以组合若干时步，提取平均数或中位数。

空洞频谱缓冲区背后的动机是在记忆中保留最近的频谱印象的同时，以高效的方式同时保持关于上下文的部分信息。

下面是使用Gammatone滤波器组构造空洞频谱的代码片段。注意这里使用的是离线处理，不过滤波器组也同样可以实时应用，在环形缓冲区中插入频谱帧。

from gammatone import gtgramimport numpy as npclass GammatoneFilterbank:    def __init__(self,                 sample_rate,                 window_time,                 hop_time,                 num_filters,                 cutoff_low):        self.sample_rate = sample_rate        self.window_time = window_time        self.hop_time = hop_time        self.num_filters = num_filters        self.cutoff_low = cutoff_low    def make_spectrogram(self, audio_samples):        return gtgram.gtgram(audio_samples,                             self.sample_rate,                             self.window_time,                             self.hop_time,                             self.num_filters,                             self.cutoff_low)    def make_dilated_spectral_frames(self,                                     audio_samples,                                     num_frames,                                     dilation_factor):        spectrogram = self.make_spectrogram(audio_samples)        spectrogram = np.swapaxes(spectrogram, 0, 1)        dilated_frames = np.zeros((len(spectrogram),                                  num_frames,                                  len(spectrogram[0])))        for i in range(len(spectrogram)):            for j in range(num_frames):                dilation = np.power(dilation_factor, j)                if i - dilation < 0:                    dilated_frames[i][j] = spectrogram[0]                else:                    dilated_frames[i][j] = spectrogram[i - dilation]        return dilated_frames

可视化空洞频谱缓冲区

嵌入缓冲区

在人类记忆的许多模式中，感官记忆经过选择性记忆这个过滤器，以避免短时记忆信息过载3。由于人类的认知资源有限，分配注意力到特定听觉感知以优化心智能量的消耗是一项优势。

我们可以通过扩展自编码器神经网络架构实现这一方法。基于这一架构，我们可以给它传入空洞频率频谱缓冲，以生成嵌入，而不是仅仅传入瞬时频率信息，这就结合了感官声音记忆和选择性注意瓶颈。为了处理序列化信息，我们可以使用序列到序列自编码器架构6。

序列到序列（Seq2Seq）模型通常使用LSTM单元编码序列数据（例如，一个英语句子）为内部表示（该表示包含整个句子的压缩“含义”）。这个内部表示之后可以解码回一个序列（例如，一个含义相同的西班牙语句子）7。

以这种方式得到的声音嵌入，可以使用算力负担低的简单前馈神经网络分析、处理。

据下图所示训练完网络后，右半部分（解码部分）可以“砍掉”，从而得到一个编码时域频率信息至压缩空间的网络。在这一领域，Y. Chung等的Audio Word2Vec取得了优秀的结果，通过应用Seq2Seq自动编码器架构成功生成了可以描述语音录音的序列化语音结构的嵌入6。使用更多样化的输入数据，它可以生成以更一般的方式描述声音的嵌入。

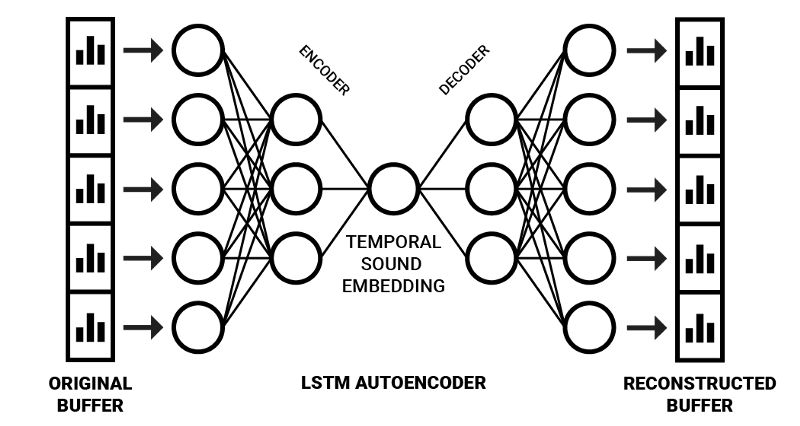
基于Keras

依照之前描述的方法，我们用Keras实现一个生成音频嵌入的Seq2Seq自动编码器。我将它称为听者网络，因为它的目的是“听取”传入的声音序列，并将它压缩为一个更紧凑的有意义表示，以供分析和处理。

我们使用了UrbanSound8K数据集（包含3小时左右的音频）训练这个网络。UrbanSound8K数据集包含归好类的环境音片段。我们使用Gammatone滤波器组处理声音，并将其分割为8时步的空洞频谱缓冲区（每个包含100个频谱滤波器）。

from keras.models import Modelfrom keras.layers import Input, LSTM, RepeatVectordef prepare_listener(timesteps,                     input_dim,                     latent_dim,                     optimizer_type,                     loss_type):    inputs = Input(shape=(timesteps, input_dim))    encoded = LSTM(int(input_dim / 2),                   activation="relu",                   return_sequences=True)(inputs)    encoded = LSTM(latent_dim,                   activation="relu",                   return_sequences=False)(encoded)    decoded = RepeatVector(timesteps)(encoded)    decoded = LSTM(int(input_dim / 2),                   activation="relu",                   return_sequences=True)(decoded)    decoded = LSTM(input_dim,                   return_sequences=True)(decoded)    autoencoder = Model(inputs, decoded)    encoder = Model(inputs, encoded)    autoencoder.compile(optimizer=optimizer_type,                        loss=loss_type,                          metrics=['acc'])    return autoencoder, encoder

网络架构

听者网络的损失函数使用均方误差，优化算法使用Adagrad，在一张NVIDIA GTX 1070上训练了50个epoch，达到了42%的重建精确度。因为训练耗时比较长，所以我在训练进度看起来还没有饱和的时候就停止了训练。我很想知道，基于更大的数据集和更多算力资源训练后这一模型表现如何。

肯定还有很多可以改进的地方，不过下面的图像表明，在3.2的压缩率下，模型捕捉到了输入序列的大致结构。