数据并行化对神经网络训练有何影响？谷歌大脑进行了实证研究

近期的硬件发展实现了前所未有的数据并行化，从而加速神经网络训练。利用下一代加速器的最简单方法是增加标准小批量神经网络训练算法中的批大小。最近谷歌大脑发表了一篇论文，旨在通过实验确定在训练阶段增加批大小的作用，评价指标是得到目标样本外误差所需的训练步数。最后，批大小增加到一定量将不再减少所需训练步数，但批大小和训练步数之间的确切关系对从业者、研究者和硬件设计人员来说非常重要。谷歌大脑研究不同训练算法、模型和数据集中批大小和训练步数之间关系的变化，以及工作负载之间的最大变化。该研究还解决了批大小是否影响模型质量这一问题。

神经网络在解决大量预测任务时非常高效。在较大数据集上训练的大型模型是神经网络近期成功的原因之一，我们期望在更多数据上训练的模型可以持续取得预测性能改进。尽管当下的 GPU 和自定义神经网络加速器可以使我们以前所未有的速度训练当前最优模型，但训练时间仍然限制着这些模型的预测性能及应用范围。很多重要问题的最佳模型在训练结束时仍然在提升性能，这是因为研究者无法一次训练很多天或好几周。在极端案例中，训练必须在完成一次数据遍历之前终止。减少训练时间的一种方式是提高数据处理速度。这可以极大地促进模型质量的提升，因为它使得训练过程能够处理更多数据，同时还能降低实验迭代时间，使研究者能够更快速地尝试新想法和新配置条件。更快的训练还使得神经网络能够部署到需要频繁更新模型的应用中，比如训练数据定期增删的情况就需要生成新模型。

数据并行化是一种直接且常用的训练加速方法。本研究中的数据并行化指将训练样本分配到多个处理器来计算梯度更新（或更高阶的导数信息），然后对这些局部计算的梯度更新求和。只要训练目标函数可分解为在训练样本上的和，则数据并行化可以适用于任意模型，应用到任意神经网络架构。而模型并行化（对于相同的训练样本，将参数和计算分配到不同处理器）的最大程度则依赖于模型大小和结构。尽管数据并行化易于实现，但大规模系统应该考虑所有类型的并行化。这篇论文主要研究在同步训练设置下数据并行化的成本和收益。

神经网络训练硬件具备越来越强大的数据并行化处理能力。基于 GPU 或定制 ASIC 的专门系统辅以高性能互连技术使得能够处理的数据并行化规模前所未有地大，而数据并行化的成本和收益尚未得到深入研究。一方面，如果数据并行化能够显著加速目前的系统，我们应该构建更大的系统。另一方面，如果额外的数据并行化收益小、成本高，则我们在设计系统时或许需要考虑最大化串行执行速度、利用其他并行化类型，甚至优先考虑能量使用、成本。

该研究尝试对数据并行化对神经网络训练的影响进行大量严谨的实验研究。为了实现该目标，研究者考虑目前数据并行化局限条件下的实际工作负载，尝试避免假设批大小函数对最优元参数的影响。该研究主要关注小批量随机梯度下降（SGD）的变体，它们是神经网络训练中的主要算法。该研究的贡献如下：

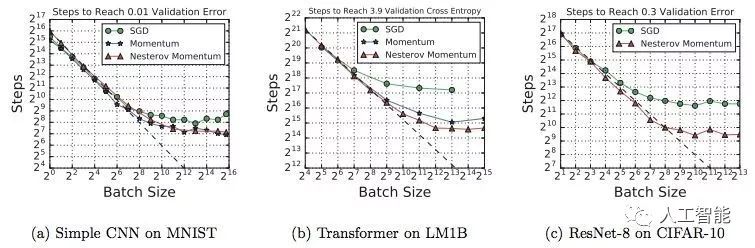
1. 该研究展示了批大小和达到样本外误差所需训练步数之间的关系在六个不同的神经网络家族、三种训练算法和七个不同数据集上具备同样的特征。

具体来说，对于每个工作负载（模型、训练算法和数据集），增加批大小最初都会导致训练步数的下降，但最终增加批大小将无法减少训练步数。该研究首次通过实验验证不同模型、训练算法和数据集上批大小与训练步数的关系，其分别调整每个批大小的学习率、动量和学习率调度器。

2. 该研究证明最大有用批大小因工作负载而异，且依赖于模型、训练算法和数据集的特性。具体而言，

带动量（和 Nesterov 动量）的 SGD 能够比普通的 SGD 更好地利用较大的批大小，未来可以研究其他算法的批大小扩展特性。

一些模型在允许训练扩展至更大的批大小方面优于其他模型。研究者将实验数据和不同模型特性与最大有用批大小之间的关系结合起来，表明该关系与之前研究中表达的不同（如更宽的模型未必能够更好地扩展至更大的批大小）。

数据集对最大有用批大小的影响不如模型和训练算法的影响，但该影响并非一贯依赖于数据集规模。

3. 训练元参数的最优值（如学习率）并非一直遵循与批大小的简单关系，尽管目前有大量启发式方法可以调整元参数。学习率启发式方法无法处理所有问题或所有批大小。假设简单的启发式方法（如随着批大小的变化对学习率进行线性扩展）可能导致最差解或对规模远远小于基础批大小的批量进行离散训练。

4. 该研究回顾了之前研究中使用的实验方案，部分解决了增加批大小是否降低模型质量这一问题。研究人员假设不同批大小对应的计算预算和元参数选择能够解释文献中的诸多分歧，然后发现没有证据能够证明批大小与模型质量下降存在必然关系，但是额外的正则化方法在批量较大的情况下变得更加重要。

实验

实验所用数据集如下所示：

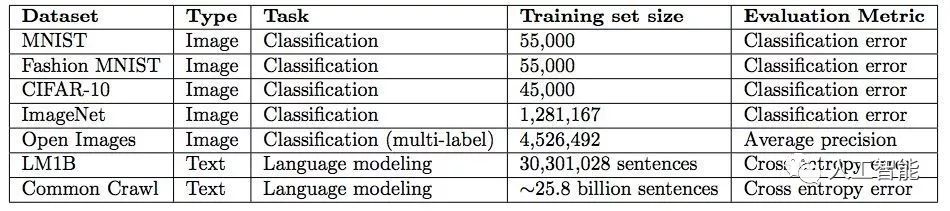
实验所用模型：

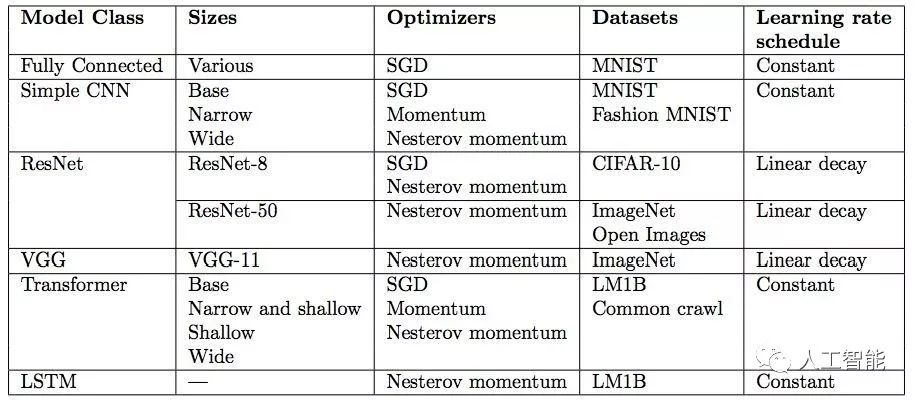
实验依赖大量元参数调整，如学习率、动量和学习率调度器。在每次实验中，研究者检查最佳试验与元参数搜索空间边界是否太过接近，从而验证元参数搜索空间。

图 1：对于上图中所有问题，训练步数与批大小之间的关系具备同样的特征。

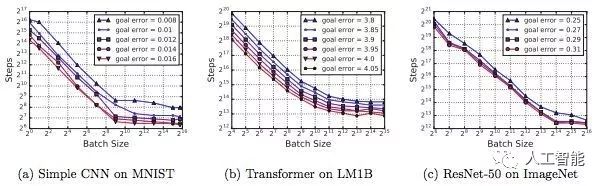
图 2：对于不同（相近）性能目标，Steps-to-result 图具备类似形式。

一些模型能够更好地利用大批量

如下图所示：

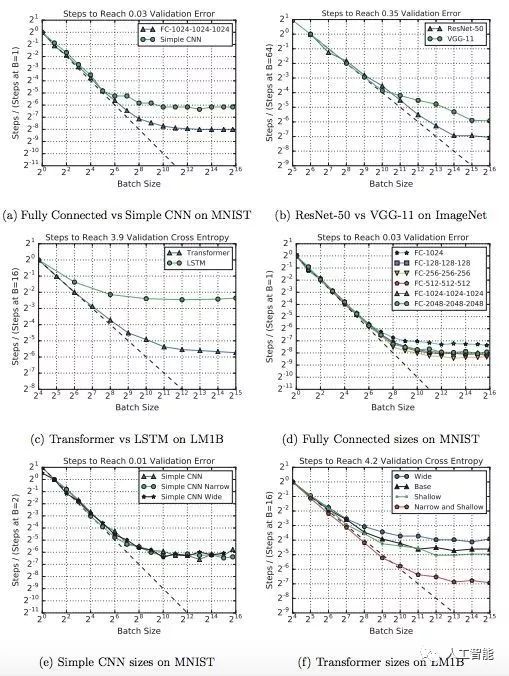
图 3：a-c 展示了在相同数据集上，一些模型架构能够从大批量中获益更多。d、f 展示了宽度和深度变化会影响模型利用大批量的能力，但是该情况并不适用于所有模型架构。图中所有的 MNIST 模型都使用了 mini-batch SGD，而其他模型使用了带 Nesterov 动量的 SGD。每个图的目标验证误差允许所有模型变体都能够达到目标误差。

带动量的 SGD 可在大批量上实现完美扩展，但在小批量上能力与普通 SGD 相当。

如下图所示：

数据集对最大有用批大小有影响，但影响程度可能不如模型或优化器

图 5：数据集对最大有用批大小有影响。

图 6：数据集大小的影响。

正则化在某些批大小上更加有用

图 7：上图是 ImageNet 数据集上的 ResNet-50 模型。每个点对应不同的元参数，因此每个点的学习率、Nesterov 动量和学习率调度器都是独立选择的。每个批大小的训练预算是固定的，但是不同批大小的训练预算不同。

最佳学习率和动量随批大小的变化而改变

图 8：最佳学习率未必遵循线性或平方根扩展启发式方法。

图 9：在固定训练数量的 epoch 中，达到目标误差的元参数空间区域随着批大小增加而缩小。

图 10：在固定的训练步数下，达到目标误差的元参数空间区域随着批大小增加而扩大。

解的质量更多地依赖计算预算而不是批大小

图 12：验证误差更多地依赖计算预算，而非批大小。

实验缺陷

在元参数调整时难免会有一定程度的人类判断。研究分析没有考虑到取得目标误差的鲁棒性。