

机器学习的logistic函数和softmax函数总结
电子说
描述
前言
本文简单总结了机器学习最常见的两个函数,logistic函数和softmax函数。首先介绍两者的定义和应用,最后对两者的联系和区别进行了总结。
目录
1. logisitic函数
2. softmax函数
3. logistic函数和softmax函数的关系
4. 总结
logistic函数
1.1 logistic函数定义
logsitic函数也就是经常说的sigmoid函数,几何形状也就是一条sigmoid曲线。
logistic函数的定义如下:
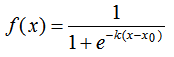
其中,x0表示了函数曲线的中心(sigmoid midpoint),k是曲线的坡度,表示f(x)在x0的导数。
对应的几何形状:
1.2 logistic函数的应用
logistic函数在统计学和机器学习领域应用最为广泛或最为人熟知的肯定是逻辑斯蒂回归模型,逻辑斯蒂回归(Logisitic Regression,简称LR)作为一种对数线性模型被广泛地应用于分类和回归场景中,此外,logistic函数也是神经网络中最为常用的激活函数,即sigmoid函数 。
logistic函数常用作二分类场景中,表示输入已知的情况下,输出为1的概率:
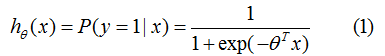
其中,为分类的决策边界。另一类的生成概率:
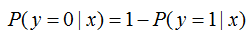
softmax函数
2.1 softmax函数的定义
softmax函数是logistic函数的一般形式,本质是将一个K维的任意实数向量映射成K维的实数向量,其中向量中的每个元素取值都介于(0,1)之间,且所有元素的和为1。
softmax函数的表达式:
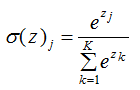
2.2 softmax函数的应用
softmax函数经常用在神经网络的最后一层,作为输出层,进行多分类。公式如下:
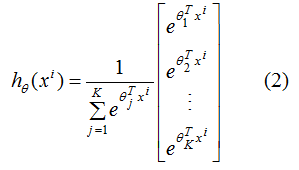
(2)式含义:输入样本为,输出向量的每个元素为K个类别中每个类的生成概率,其中为第 j类的模型参数,为归一化项,使得所有概率之和为1。
2.3 softmax回归模型的参数冗余
我们对(2)式减去向量,此时,输入样本为,输出为第j类的生成概率:
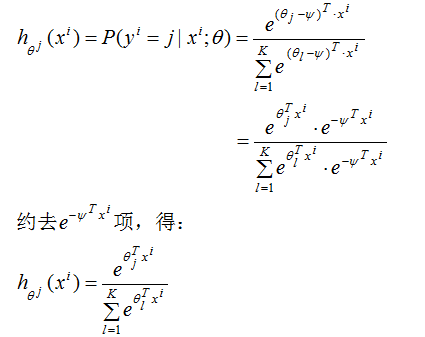
由上式可得,从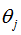 中减去
中减去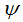 完全不影响假设函数的预测结果,表明softmax回归模型存在冗余的参数,模型最优化结果存在多个参数解。
完全不影响假设函数的预测结果,表明softmax回归模型存在冗余的参数,模型最优化结果存在多个参数解。
解决办法:对softmax回归模型的损失函数引入正则化项(惩罚项),就可以保证得到唯一的最优解。
logistic函数和softmax函数的关系
相同点:
(1)最优模型的学习方法
我们常用梯度下降算法来求模型损失函数的最优解,因为softmax回归是logistic回归的一般形式,因此最优模型的学习方法相同。
logistic回归的损失函数的偏导数:
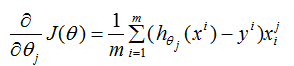
参数更新:
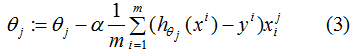
由(3)式可知,当样本实际标记值为1时,则会以增大的方向更新;样本实际标记值为-1时,则会以减小的方向更新。同理,softmax回归参数的思想也大致相同,使得模型实际标记的第K类的生成概率接近于1。
(2)二分类情况
logistic回归针对的是二分类情况,而softmax解决的是多分类问题,若softmax回归处理的是二分类问题,则表达式如下:
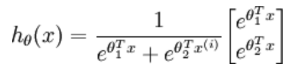
利用2.3节的softmax回归的参数冗余特点,参数向量减去向量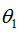 ,得到:
,得到:
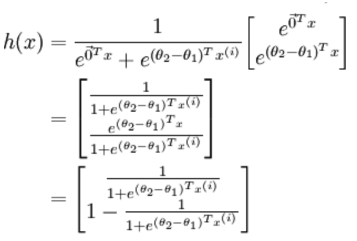
令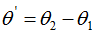 ,上式可表示为:
,上式可表示为:
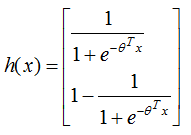
与logistic二分类的表达式一致,因此,softmax回归与logistic回归的二分类算法相同 。
不同点:
多分类情况
logistic回归是二分类,通过“1对1(one vs one)“分类器和”1对其他(one vs the rest)“分类器转化为多分类。但是,这两种方法会产生无法分类的区域,该区域属于多个类,如下图:
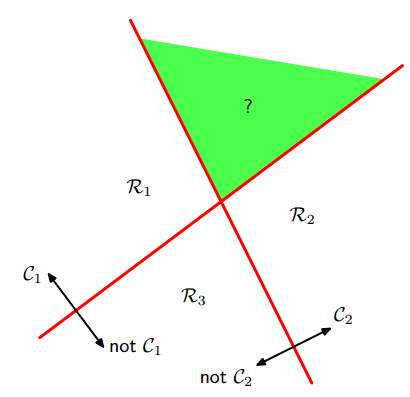
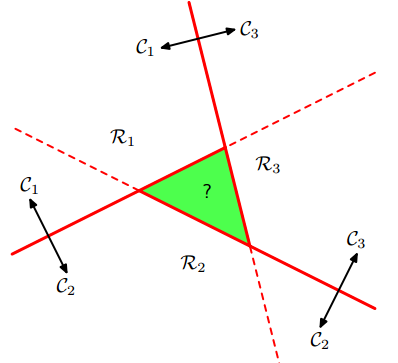
左图是1对多的分类情况,右图是1对1的分类情况,绿色为无法分类的区域。
softmax回归进行的多分类,输出的类别是互斥的,不存在无法分类的区域,一个输入只能被归为一类;
logistic多分类的解决办法:若构建K类的分类器,通过创建K类判定函数来解决无法分类的问题。假定K类判定函数为,对于输入样本x,

则样本属于第k类。
总结
logisitc函数常用于二分类和神经网络的激活函数,softmax函数常用于神经网络的输出层,进行多分类。logistic多分类回归可通过设置与类数相同的判别函数来避免无法分类的情况。
-
机器学习实战之logistic回归2020-09-29 2887
-
WinCC标准函数总结2010-10-09 880
-
matlab牛逼函数总结2015-11-06 763
-
函数指针和指针函数定义2016-01-11 777
-
MATLAB常用函数总结(表格)2016-01-21 638
-
arduino学习必须掌握的函数资料下载2018-04-26 876
-
机器学习算法之一:Logistic 回归算法的优缺点2018-06-23 38176
-
机器学习经典损失函数比较2018-06-13 9250
-
C语言入门教学之函数资料总结免费下载2018-10-23 965
-
机器学习的Softmax定义和优点2020-03-15 5294
-
机器学习和深度学习中分类与回归常用的几种损失函数2020-10-09 7109
-
c++中构造函数学习的总结(一)2020-12-24 1223
-
机器学习中若干典型的目标函数构造方法2020-12-26 5011
-
vc++-CDC常用函数总结2021-09-27 620
-
机器学习找一个好用的函数的原因是什么2022-11-02 1450
全部0条评论

快来发表一下你的评论吧 !

