如何用TensorFlow概率编程工具包开发深度学习

通用电气的贝克休斯公司 Baker Hughes（BHGE）是世界领先的全流程石油和天然气公司，致力于寻求更佳的方式向世界输送能源。BHGE 的数字团队开发了企业级别的，依靠人工智能驱动的 SaaS 解决方案，以提高效率并减少石油和天然气行业的非生产时间。要考虑关键任务问题，诸如预测燃气轮机故障或优化石化厂等大型的系统；这些问题需要大规模构建和维护复杂的分析。为此，我们开发了一种分析驱动型战略计划，为客户实现全公司数字化改造。

多年来一直帮助工业界解决最棘手问题，使我们掌握了最优雅持久的解决方案：

领域知识 

传统机器学习

概率技术

深度学习

之前难以处理的问题类别现在可以通过将一些看似毫无关系的技术并将它们与现代可扩展的软硬件组合在一起部署来解决。我们与 TensorFlow Probability（TFP）团队和 Google 的 Cloud ML 团队的合作加速了我们大规模开发和部署这些技术的过程。

我们想将这些节点发生的创新通过这一系列的文章进行展示，希望以此激发在概率深度学习技术的工业应用中实现爆炸性增长。在这里你们可以看到我们在 Google Next 2018 展示的这些应用程序示例集。

需要概率深度学习

数十年来，基于物理的（即基于领域的）分析已经被成功地应用于设计和操作航空航天、汽车、石油和天然气等行业的系统。它们提供了一个行之有效的方法，能够从一些观察中概括复杂的行为。牛顿的运动方程可以用来精确地预测原子和星系的运动。然而，对现实世界问题的创新解决方案需要将这些律法与解决未知因素的有效方法相结合。要捍卫科学，明确地追踪我们信念的确定性至关重要。

我们举一个采用射弹轨迹的 “简单” 例子。为了预测抛射物落地的位置，进行准确预测所需的唯一观察（数据）是投射抛射物的速度（速度和角度）。然而，在初始角度和风速中增加一个很小的不确定性（~5％）会给射弹落地的位置带来巨大的不确定性（~200％），如下图所示。

即使是简单的系统，也可以通过不确定性进行准确的预测；想象一下优化大型非线性系统得有多么复杂！

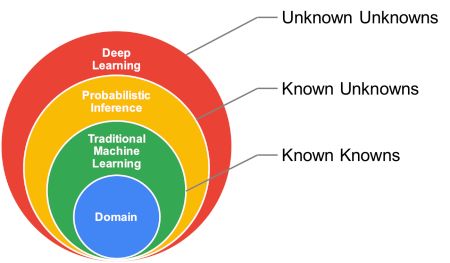
Digital Twin 是 BHGE Analytics 团队在解决实际工业问题方面经过多年磨练的结构。我们将其定义为物理系统的数字表示，不断调整用以表示当前条件并预测未来状态。如下图所示，构建数字孪生所需的三大支柱是领域知识，概率推理和深度学习：

领域专业知识（即物理学）与传统 ML 相结合，使我们能够精确地解决已知问题，换句话说，已知的知识。通过传统的 ML，我们指的是诸如多项式回归，核密度方法和状态空间估计方法（例如卡尔曼滤波器）之类的技术。在各种热机械载荷下预测零件中裂纹的长度是领域专业知识的一个例子：它需要彻底了解问题的物理特性以及温度和压力等边界条件的知识。即使很好地理解了这种现象，也需要几种传统的 ML 技术来计算特定于问题的系数（例如材料特性）。

概率推理提供了一种量化不确定性的系统方法，即已知的未知数。在上面的例子中，除了理解这些现象外，我们还需要考虑测量的不确定性和制造变异性等非模型因素。众所周知，系统中存在会影响裂纹扩展的可变性（不确定性）。预测裂缝长度然后成为不确定性量化练习。更具体地说，当我们在测量中增加不确定性时，材料特性校准成为概率推理问题。

深度学习和现代 ML 有潜力识别和预测未知的模式和行为，也就是未知的未知。在裂缝传播实例中，即使概率推理与领域模型相结合，我们也可以预测裂缝仅在具有已知不确定性的特定负载条件下传播。考虑基于自动编码器的异常检测模型，该自动编码器监视负载条件以及设备上的各种其他条件。这种深度学习模型可以捕获基于物理的模型无法获取的异常情况。我们将此预测表示为未知的未知，原因是因为我们没有关于异常的任何数据来训练模型。虽然深度学习模型训练正常操作的数据（以及一些验证异常），但它可以捕捉到之前未观察到的正常行为的任何偏差。这是深度学习模型派上用场的众多例子之一。可以说，在某些情况下，基于传统技术（如 PCA 重建误差）的简单异常检测模型也可以解决问题。根据我们的经验，当已知的过程特征与这些方法的简化假设一致时，更简单的技术可以提供与深度学习模型类似甚至更好的性能，从而导致已知的异常。当异常事件突如其来毫无征兆时 - 当你之前从没有看到特定的故障模式时，深度学习模型的表现真的出类拔萃。

在本文中，我们将重点关注在预测已知未知数的领域模型的概率推断。我们将演示贝叶斯校准的能力，其中裂缝传播问题被公式化为基于物理的概率推理模型。

概率深度学习使我们能够在 “自学” 包中利用上面强调的所有功能。我们将在随后的博客中讨论使用 TFP 进行概率深度学习，其中包括模型差异，异常检测，缺失数据估计和时间序列预测。

预测组件的寿命：概率性裂缝传播示例

预测易于开裂的部件的寿命是一个老生常谈的问题，断裂力学界已经研究过。裂缝传播模型是工程系统的预测和健康管理（PHM）解决方案的核心。题为《预测与工程系统健康管理：简介》一书提供了一个很好的例子，说明现实世界数据如何用于校准工程模型。通过下面的示例，我们希望激发使用结合概率学习技术和工程领域模型的 “混合模型”。

疲劳裂纹扩展现象可以用巴黎定律建模。巴黎定律通过以下等式将裂纹扩展速率（da / dN）与应力强度因子（ΔK=Δσ√）联系起来：

其中 a 是裂纹长度，N 是加载循环次数，σ 是应力，（C，m）是材料属性。

将巴黎定律与特定几何和加载配置相结合，我们得出裂缝大小的分析公式，作为加载循环的函数，如下所示：

其中 aₒ 是初始裂缝长度。通过了解给定应用中的 aₒ 和因子 Δσ√，可以使用等式 2 来计算未来裂缝的大小，假设应用将随时间累积 N 个周期。可以将该预测的裂缝长度与安全操作的阈值进行比较。例如，如果预测的裂缝长度超过几何极限（例如，部件厚度的一半），那就说明该修理了。

在给定裂缝长度 a 与加载循环 N 数据的情况下，需要针对每个物理组件校准参数 C 和 m。换句话说，考虑到现场测量的裂缝，我们希望推断出 C 和 m，这样就可以估算出在裂缝长度变大到一定程度，在部件失效的风险之前，可以安全地运行多少个循环。

在本例中，我们将使用由 Kim，An 和 Choi 编写的 PHM 书中的样本数据集，演示使用 TFP 进行 C 和 m 的概率校准。在 BHGE Digital，我们利用 Depend-on-Docker 项目实现分析开发的自动化。此处提供了此类自动化的示例，其中包含以下示例的完整代码。

如下图所示，我们使用了 Kim，An 和 Choi 的 PHM 书中的表 4.2 中提供的数据集。对于大多数裂缝传播数据集而言，从观察到的数据点来看，潜在趋势并不十分明显。

对于贝叶斯校准，我们需要定义校准变量的先验分布。在实际应用中，这些先验可以由主题专家通知。对于这个例子，我们假设 C 和 m 都是高斯和独立的：

在 TFP 中，我们可以对此信息进行如下编码：

1    prio_par_logC = [-23., 1.1] # [location, scale] for Normal Prior

2    prio_par_m = [4., 0.2] # [location, scale] for Normal Prior    

3    rv_logC = tfd.Normal(loc=0., scale=1., name='logC_norm')  

4    rv_m = tfd.Normal(loc=0., scale=1., name='m_norm')

我们为两个变量定义了外部参数和标准正态分布，只是为了从标准化空间中进行采样。因此，在计算裂缝模型时，我们需要对两个随机变量进行去标准化。

现在我们定义被校准的随机变量的联合对数概率以及由等式 2 定义的相关裂缝模型：

1    def joint_log_prob(cycles, observations, y0, logC_norm, m_norm):

2        # Joint logProbability function for both random variables and observations.

3        # Some constants    

4        dsig = 75.

5        B = tf.constant(dsig * np.pi**0.5, tf.float32)

6        # Computing m and logC on original space

7        logC = logC_norm * prio_par_logC[1]**0.5+ prio_par_logC[0] #

8        m = m_norm * prio_par_m[1]**0.5 + prio_par_m[0]

9

10        # Crack Propagation model

11        crack_model =(cycles * tf.exp(logC) * (1 - m / 2.) * B**m + y0**(1-m / 2.))**(2. / (2. - m))

12        y_model = observations - crack_model

13

14

15        # Defining child model random variable

16        rv_model = tfd.Independent(       

17         tfd.Normal(loc=tf.zeros(observations.shape), scale=0.001),       

18        reinterpreted_batch_ndims=1, name = 'model')

19        # Sum of logProbabilities

20        return rv_logC.log_prob(logC_norm) + rv_m.log_prob(m_norm) + rv_model.log_prob(y_model)

最后，是时候设置采样器并运行 TensorFlow 会话了：

1    # This cell can take 12 minutes to run in Graph mode

2    # Number of samples and burnin for the MCMC sampler

3    samples = 10000

4    burnin = 10000

5

6    # Initial state for the HMC

7    initial_state = [0., 0.]

8    # Converting the data into tensors

9    cycles = tf.convert_to_tensor(t_,tf.float32)

10    observations = tf.convert_to_tensor(y_,tf.float32)

11    y0 = tf.convert_to_tensor(y_[0], tf.float32)

12    # Setting up a target posterior for our joint logprobability

13    unormalized_target_posterior= lambda *args: joint_log_prob(cycles, observations, y0, *args)

14    # And finally setting up the mcmc sampler

15    [logC_samples, m_samples], kernel_results = tfp.mcmc.sample_chain(

16        num_results= samples,

17        num_burnin_steps= burnin,

18        current_state=initial_state,

19        kernel= tfp.mcmc.HamiltonianMonteCarlo(

20                target_log_prob_fn=unormalized_target_posterior,

21                step_size = 0.045,

22                num_leapfrog_steps=6))

23

24

25    # Tracking the acceptance rate for the sampled chain

26    acceptance_rate = tf.reduce_mean(tf.to_float(kernel_results.is_accepted))

27

28    # Actually running the sampler

29    # The evaluate() function, defined at the top of this notebook, runs `sess.run()

30    # in graph mode and allows code to be executed eagerly when Eager mode is enabled

31    [logC_samples_, m_samples_, acceptance_rate_] = evaluate([ 

32        logC_samples, m_samples, acceptance_rate])

33

34    # Some initial results

35    print('acceptance_rate:', acceptance_rate_) 

值得注意的是，尽管我们开始使用 C 和 m 的两个独立高斯分布，但后验分布是高度相关的。这种相关性的产生是因为解空间规定对于 m 的高值，唯一有物理意义的结果是 Cand 的小值，反之亦然。如果我们使用任意数量的确定性优化技术来找到适合此数据集的 C 和 m 的 “最佳拟合”，那么根据我们的起点和约束，我们最终会得到一些位于直线上的值。执行概率优化（也就是贝叶斯校准）为我们提供了可以解释数据集的所有可能解决方案的全局视图。

后验抽样后进行预测  

现在到了最后一步，我们将后验函数定义为对数正态分布，期望由物理模型定义：

已知损坏（在这种情况下为裂缝长度）是倾斜的，因此对数正常或 Gumbel 分布通常用于模拟损伤。在 TFP 中表达模型如下所示：

1    def posterior(logC_samples, m_samples, time):

2        n_s = len(logC_samples)

3        n_inputs = len(time)

4

5        # Some Constants

6        dsig = 75.

7        B = tf.constant(dsig * np.pi**0.5, tf.float32)

8

9        # Crack Propagation model - compute in the log space

10

11        y_model =(

12                time[:,None]  * 

13                tf.exp(logC_samples[None,:])*

14                (1-m_samples[None,:]/2.0) *B**m_samples[None,:] +y0** (1-m_samples[None,:]/2.0))**(2. / (2. - m_samples[None,:]))    

15        noise = tfd.Normal(loc=0., scale=0.001)    

16        samples = y_model + noise.sample(n_s)[tf.newaxis,:]

17        # The evaluate() function, defined at the top of this notebook, runs `sess.run()`     

18        # in graph mode and allows code to be executed eagerly when Eager mode is enabled

19        samples_ = evaluate(samples)

20        return samples_ 

21

22    # Predict for a range of cycles

23    time = np.arange(0, 3000, 100)

24    y_samples = posterior(logC_samples_scale, m_samples_scale, time) 

25    print(y_samples.shape)

如下所示，使用混合物理概率模型的裂缝长度的 95％ 不确定界限的预测平均值。很显然，该模型不仅捕获平均行为，还捕获每个时间点模型预测的不确定性估算。当我们偏离观察时，模型预测中的不确定性呈指数增长趋势。

下一步

我们选择这个例子十分小心，来对概率模型做一个介绍。将概率模型应用于实际应用程序存在一些挑战。即使在像这里所展示的简单问题中，如果我们放松高斯先验的假设，那么解决方案也会变得棘手。如果读者感到好奇，可以尝试使用统一先验来观察一下模型预测能力急剧下降的情况。

另一个微妙点是定义可能性的方式。我们选择直接在预测误差上定义它，而不是预测值。请注意，下面在 “基于预测误差的可能性” 中描述的各个蓝线是模型预测误差的样本。直接将公式更改为模型预测 - 而不是预测误差 - 会产生非单调的非物理结果，如 “基于实际预测的可能性 ” 所示。我们称这些结果是非物理的，因为裂缝长度不会随着时间的推移而减小。如果我们只查看上面显示的 “模糊” 百分位数视图，我们可能不会注意到模型公式中可能导致较大预测误差的细微差别。我们将在下一篇文章中解决其中一些更实际的挑战及其缓解措施。

这是系列文章中的第一篇，旨在通过 TFP 扩展概率和深度学习技术在工业应用中的应用。我们（@sarunkarthi）很想听听关于您的应用程序的说明，并期待看到这些方法应用到更多独特的方方面面。请继续关注此文章供稿，了解有关异常检测，缺失数据估算和变异推断预测的更多更新的示例。