将预测问题简化为选择问题——Apollo车道预测详解

本节课我们将继续学习无人车的预测模块，包括预测目标车道，递归神经网络及其在目标车道的应用和轨迹的生成。

1、预测目标车道

使用车道序列框架作为目标是为了让道路上的物体生成轨迹，这是一个复杂的问题 。

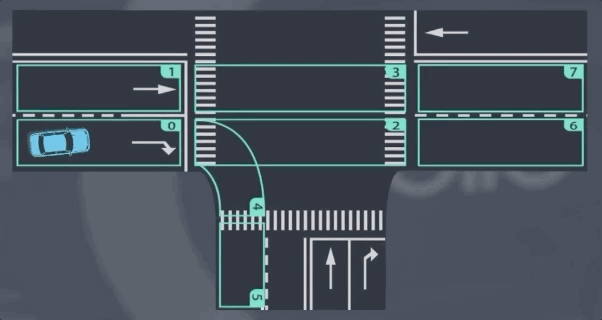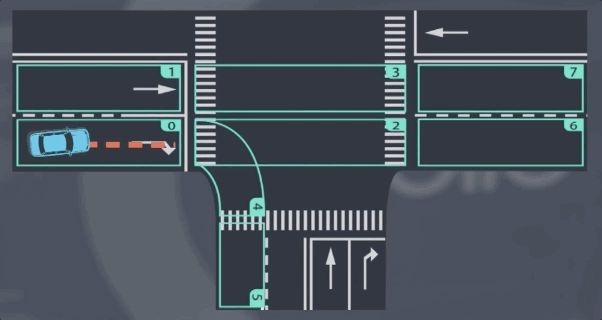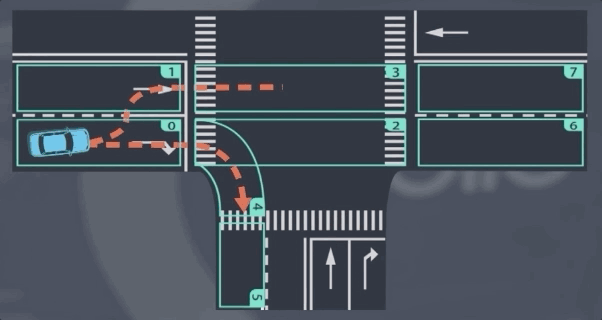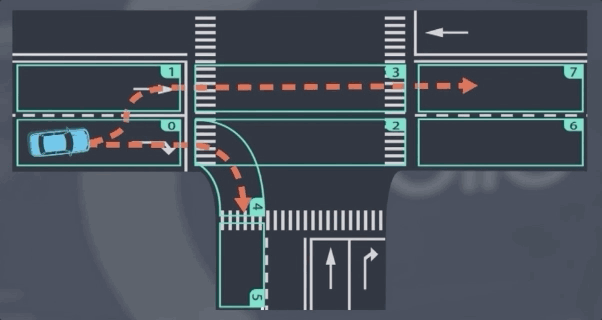
我们先从一个稍微简单的问题开始——预测车道线段之间的过渡。假设我们在车道段0中检测到一辆车，并且我们会预测在接下来的几个时间段它将如何行使。现在有两个显而易见的选择：

它可能停留在车道段0然后向右转；

或者可能转向车道段1然后直行。

这个分析实际上是我们前进的一大步——我们已经将预测问题简化为选择问题。

将“预测问题”简化为“选择问题”

我们可以通过计算每个车道序列的概率，来选择车辆最有可能选取的车道顺序。此时我们需要一个模型，将车辆状态和车道段作为输入，通过该模型的计算得出车辆可能采用每个车道序列的概率。

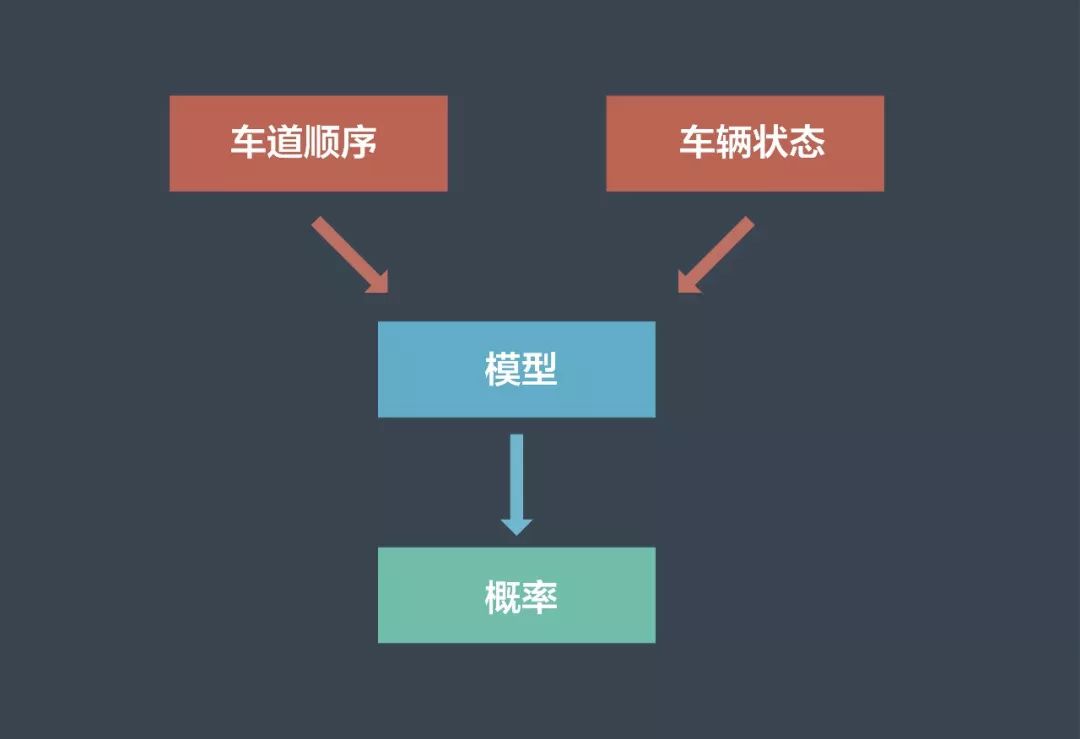
基础模型

在完成概率计算的同时，我们希望模型能够学习新的行为，因此要使用观测数据对模型进行经验性训练。在训练中，我们将真实的车辆行为提供给模型，不仅包括车道段和车辆的状态，还包括车辆最终选择哪条车道序列。当记录数据随着时间而增加，模型就能够实现自我迭代更新，精确度不断提升。

其中，每个记录将由观察对象跟随的车道段序列和对象的相关状态组成。在每个时间点，对象占用一段并具有特定的状态，整个记录由一系列车道段和对象的相关状态组成。

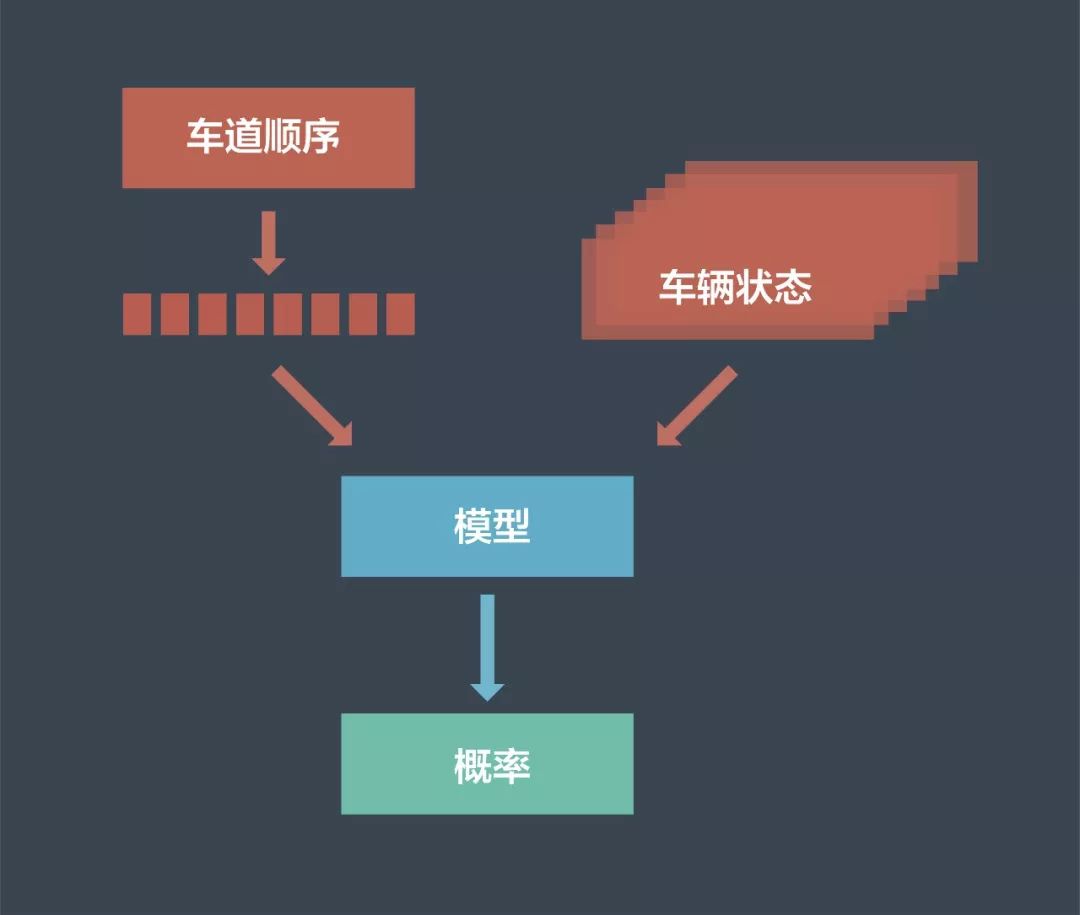
模型的经验性训练示意

2、递归神经网络

递归神经网络或 Recurrent Neural Network（以下简称 RNN）是一种利用时间序列数据特征的预测方式。在研究 RNN 之前，我们需要先来回顾一下神经网络。

神经网络是可训练的多层模型，神经网络从输入提取高级特征，并使用这些特征来计算得到输出。例如，如果你有一个神经网络来判断图像中是否包括汽车从而完成分类，网络的中间层将提取特征，如轮胎和窗户。神经网络有许多结构，一个基本的神经网络首先得到输入，随后将数据通过隐藏层，然后经过处理得到输出。这种结果有时也被称作多层感知网络或 MLP。

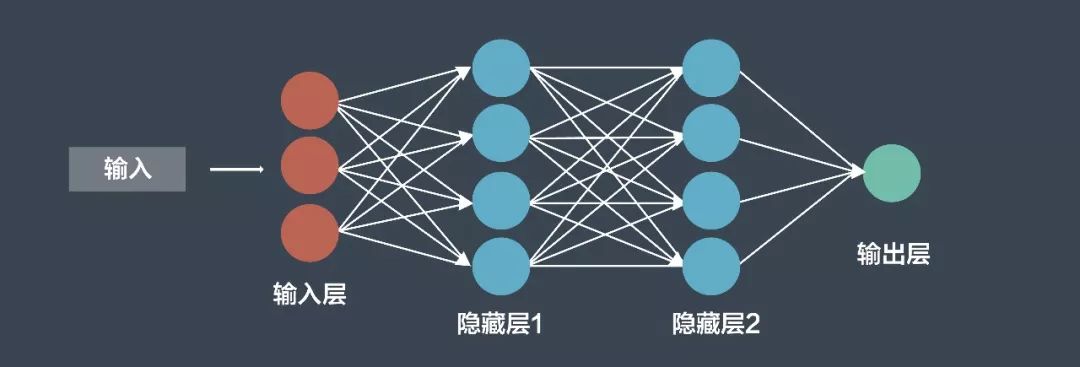
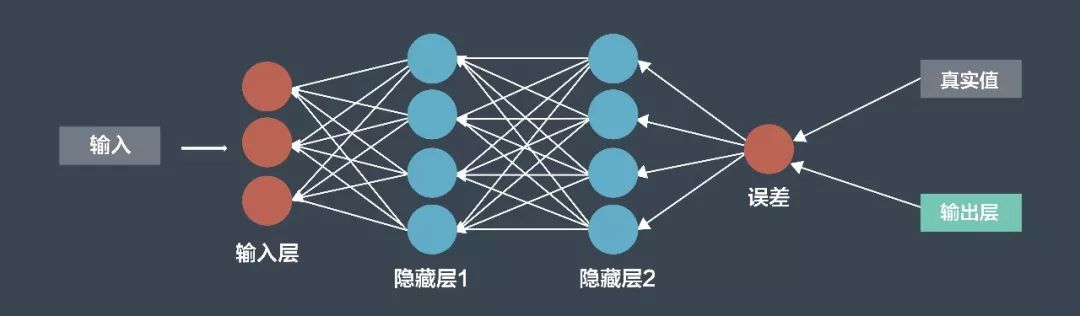
在训练过程中，会有很多训练数据输入模型，每一个数据都由原始的数据和对应的标签组成。例如，输入数据是一张图片，标签就是一个包含汽车的符号或是其他符号，神经网络从数据中学习的方式叫做后向传播。首先，神经网络得到输出并产生输出；然后，计算机比较输出与真值之间的误差；接着，这种误差回传到整个网络，中间的隐藏层根据观察到的差别权重判断调整其中的中间值。这样可以在未来提高神经网络的准确率。

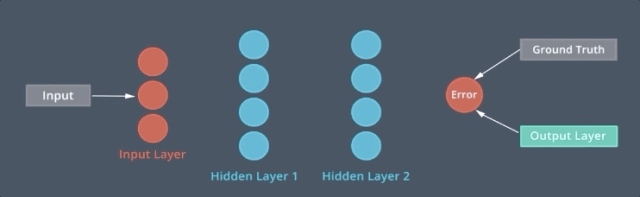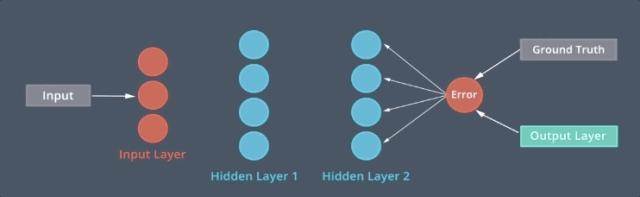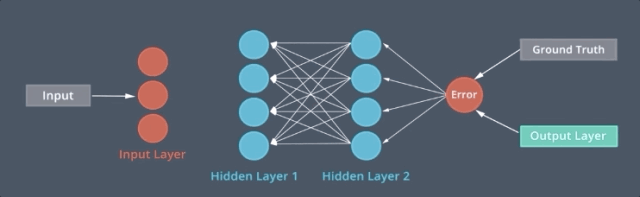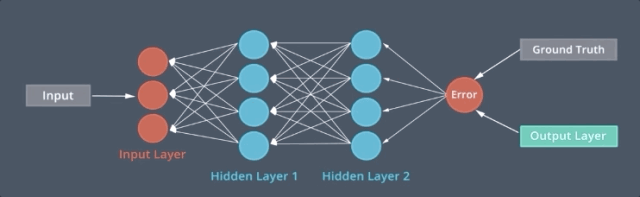
我们可以建立像这样的多重结构的递归神经网络，我们称之为 MLP 单元。从数据序列中提取出高级特征，每个 MLP 单元将序列的一个要素作为输入，并预测序列的下一个要素作为输出，为了对元素之间的顺序关系建立模型，我们在每个单元之间建立一个额外的连接，这意味着每个单元根据原始输入和前一个单元的输入进行预测，这是 RNN 的基本结构。

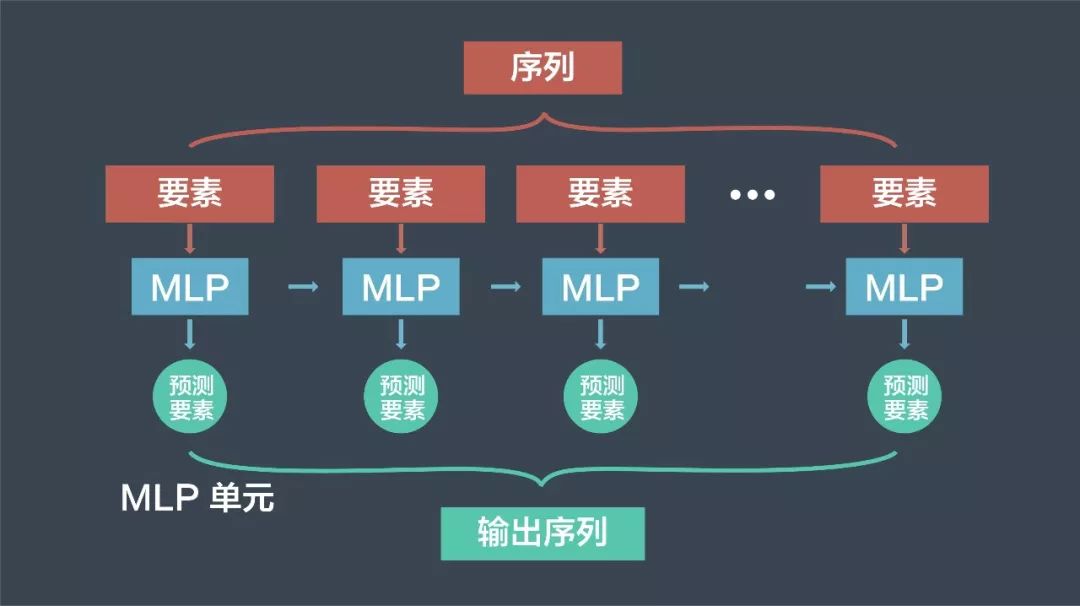
3、递归神经网络在目标车道预测的应用

Apollo 会使用 RNN 建立一个模型来预测车辆的目标车道。首先，我们为车道序列提供一个 RNN 模型，为相关车辆状态提供另一个 RNN 模型，然后连接这两个 RNN 的输出并将它们馈送到另一个神经网络，该神经网络会计算每个车道序列的概率，具有最高概率的车道序列是我们预测目标车辆将遵循的序列。

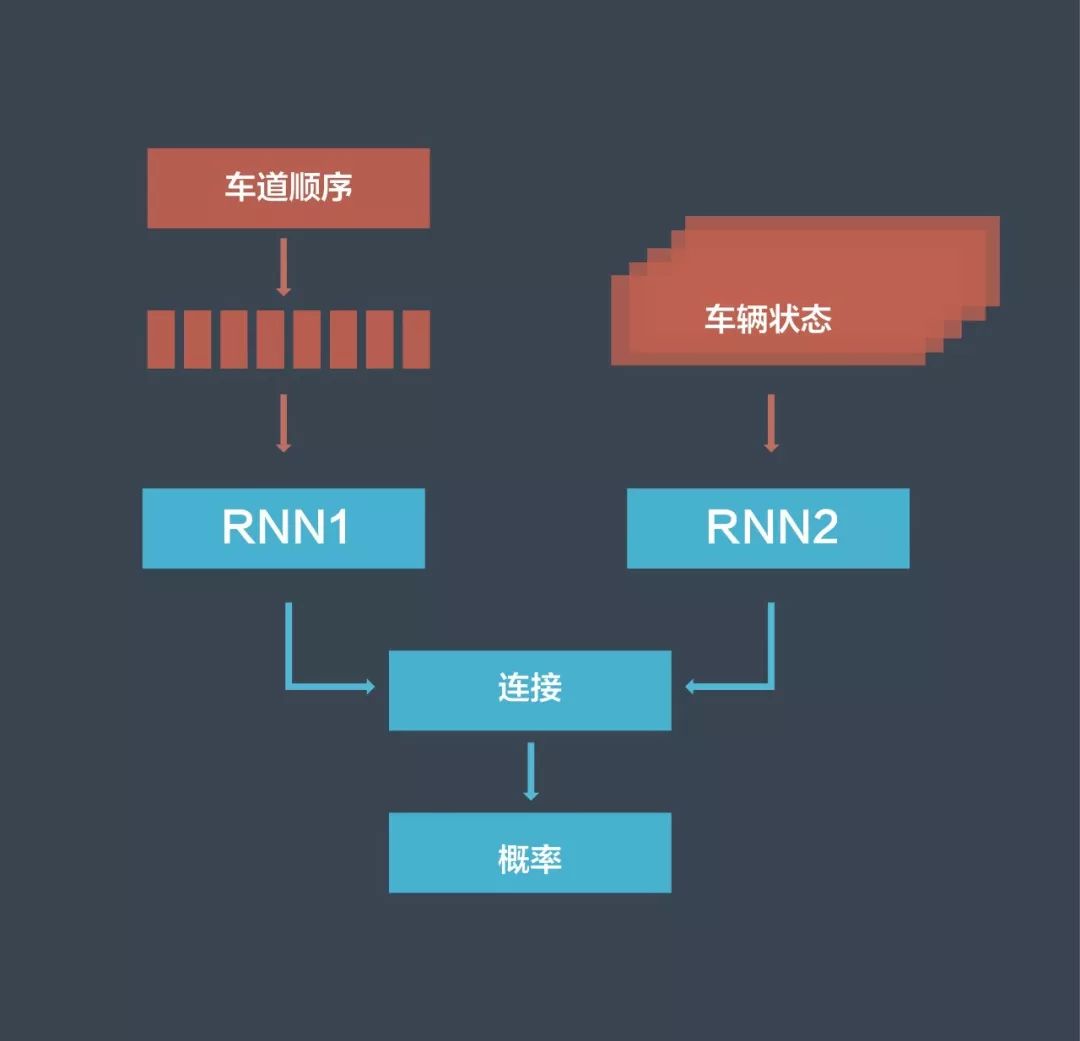
为了训练这个网络，我们使用包含一个车道序列的现有记录、相关的对象状态和一个标签，用于指示对象是否遵循此特定的车道序列。在训练中，我们比较网络输出和真值标记，并使用反向传播来训练网络。

4、轨迹生成

轨迹生成是预测的最后一步，一旦我们预测到物体的车道序列，我们就可以预测物体的轨迹。在任何两点 A 和 B 之间，物体的行进轨迹有无限的可能，我们如何预测最有可能的轨迹？

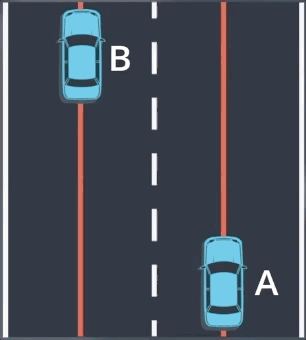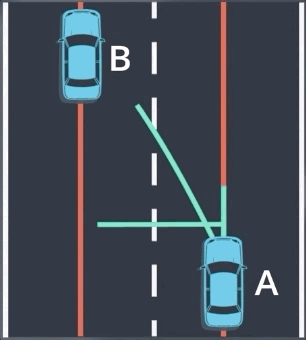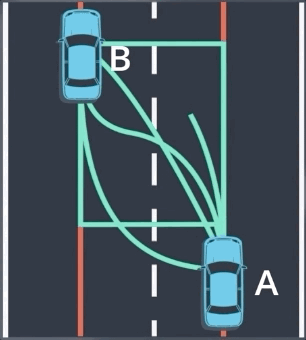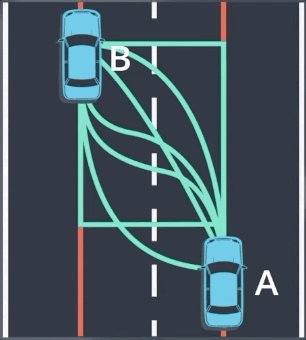
我们可以先通过设置约束条件， 来去除大部分候选轨迹。首先，我们假设汽车将与目标车道的中心对齐，去除车辆无法实际执行的轨迹，再通过考虑车辆当前的速度和加速度从剩余轨迹中进行选择。

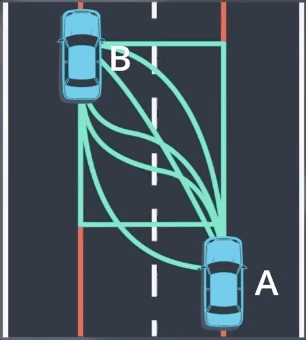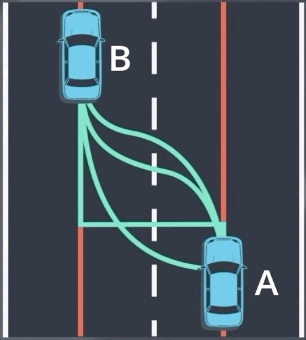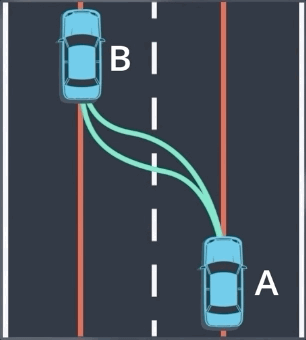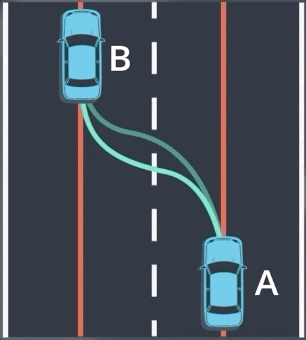
实际上，我们并没有列出所有可能的轨迹并逐一去除他们；相反，我们只是在数学理论上来应用这一想法，注意车辆在亮点的位置和方位，这两个要素表示运动模型的初始状态和最终状态，我们可以使用这两个条件来拟合一个多项式模型。

在大多数情况下，这种多项式足以进行预测。

恭喜你，你已经学会了无人车如何预测道路上物体的行为，以及如何使用轨迹来描述他们的行为。让我们回顾一下“预测”模块的主要内容：

首先，我们介绍了如何将负责的车辆运动转换为车道转换序列，这使我们能够大大减少场景的数量并更快地进行预测；

然后，我们介绍了如何使用现有观测值以车道序列表示训练神经网络来进行预测；

最后，我们将车道序列预测与车辆物理结合起来，为每个物体生成估计的轨迹，运动预测对于在规划中构建无碰撞的安全路径来说至关重要。 

希望 Apollo 预测课程的内容能让你直观地了解无人车在实际运行中的预测逻辑。