AdaBoost算法相关理论和算法介绍

作者简介

 张磊：从事AI医疗算法相关工作个人微信公众号：机器学习算法那些事（微信ID：zl13751026985）

目录

1. Boosting算法基本原理

2. Boosting算法的权重理解

3. AdaBoost的算法流程

4. AdaBoost算法的训练误差分析

5. AdaBoost算法的解释

6. AdaBoost算法的过拟合问题讨论

7. AdaBoost算法的正则化

8. 总结

本文详细总结了AdaBoost算法的相关理论，相当于深入理解AdaBoost算法，该文详细推导了AdaBoost算法的参数求解过程以及讨论了模型的过拟合问题。

AdaBoost算法的解释

AdaBoost算法是一种迭代算法，样本权重和学习器权重根据一定的公式进行更新，第一篇文章给出了更新公式，但是并没有解释原因，本节用前向分布算法去推导样本权重和学习器权重的更新公式。

1. 前向分布算法

考虑加法模型：

 

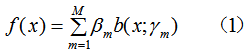
给定训练数据和损失函数L(y,f(x))的条件下，构建最优加法模型f(x)的问题等价于损失函数最小化：

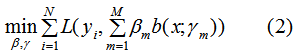
我们利用前向分布算法来求解（2）式的最优参数，前向分布算法的核心是从前向后，每一步计算一个基函数及其系数，逐步逼近优化目标函数式（2），那么就可以简化优化的复杂度。

算法思路如下：

M-1个基函数的加法模型：

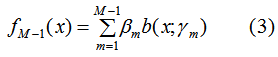
M个基函数的加法模型：

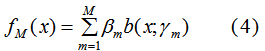
由（3）（4）得：

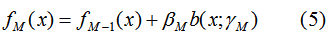
因此，极小化M个基函数的损失函数等价于：

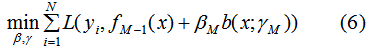
前向分布算法的思想是从前向后计算，当我们已知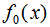的值时，可通过（6）式递归来计算第 i 个基函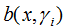数及其系数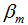，i = 1,2,...M。

结论：通过前向分布算法来求解加法模型的参数。

2. AdaBoost损失函数最小化

AdaBoost算法的强分类器是一系列弱分类器的线性组合：

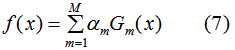
其中f(x)为强分类器，共M个弱分类器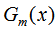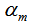，是对应的弱分类器权重。

由（7）式易知，f(x)是一个加法模型。

AdaBoost的损失函数L(y,f(x))为指数函数：

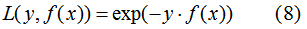
利用前向分布算法最小化（8）式，可得到每一轮的弱学习器和弱学习器权值。第m轮的弱学习器和权值求解过程：

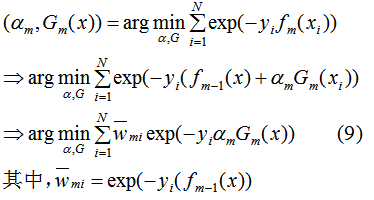
首先根据（9）式来求解弱学习器，权值α看作常数：

求解弱学习器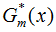后，（9）式对α求导并使导数为0，得：

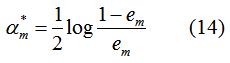
其中，α是弱学习器权值，e为分类误差率：

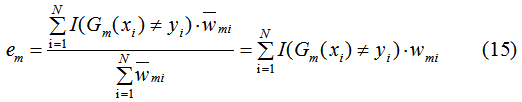
因为AdaBoost是加法迭代模型：

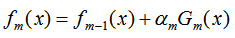
以及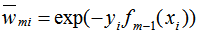，得：

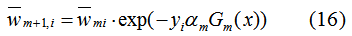
结论：式(14)(15)(16)与第一篇文章介绍AdaBoost算法的权重更新完全一致，即AdaBoost算法的权重更新与AdaBoost损失函数最优化是等价的，每次更新都是模型最优化的结果，（13）式的含义是每一轮弱学习器是最小化训练集权值误差率的结果。一句话，AdaBoost的参数更新和弱学习器模型构建都是模型最优化的结果。

AdaBoost算法的过拟合问题讨论

1. 何时该讨论过拟合问题

模型的泛化误差可分解为偏差、方差与噪声之和。当模型的拟合能力不够强时，泛化误差由偏差主导；当模型的拟合能力足够强时，泛化误差由方差主导。因此，当模型的训练程度足够深时，我们才考虑模型的过拟合问题。

2. 问题的提出

如下图为同一份训练数据的不同模型分类情况：

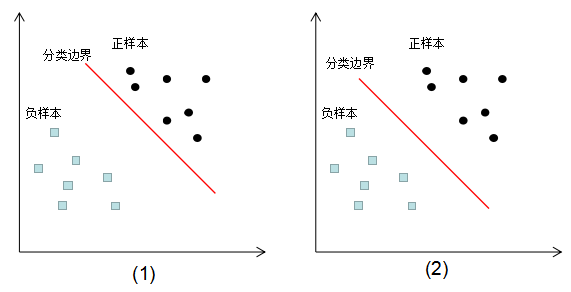
图（1）（2）的训练误差都为0，那么这两种分类模型的泛化能力孰优孰劣？在回答这个问题，我想首先介绍下边界理论（Margin Theory）。

3. 边界理论

周志华教授在《集成学习方法基础与算法》证明了：

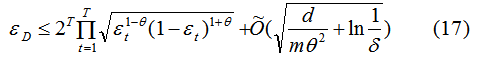
其中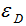，为泛化误差率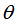，为边界阈值。

由上式可知，泛化误差收敛于某个上界，训练集的边界（Margin）越大，泛化误差越小，防止模型处于过拟合情况。如下图：

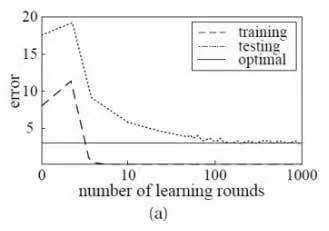
结论：增加集成学习的弱学习器数目，边界变大，泛化误差减小。

4. 不同模型的边界评估

1） 线性分类模型的边界评估

用边界理论回答第一小节的问题

线性分类模型的边界定义为所有样本点到分类边界距离的最小值，第一小节的图（b）的边界值较大，因此图（b）的泛化能力较好。

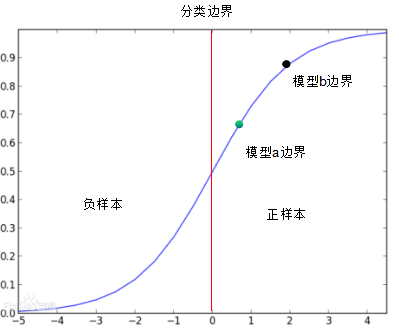
2） logistic分类模型的边界评估

logistic分类模型的边界定义为所有输入样本特征绝对值的最小值，由下图可知，模型b边界大于模型a边界，因此，模型b的泛化能力强于模型a 。

3）AdaBoost分类模型边界评估

AdaBoost的强分类器：

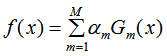
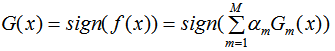
AdaBoost的边界定义为f(x)的绝对值，边界越大，泛化误差越好。

当训练程度足够深时，弱学习器数目增加，f(x)绝对值增加，则泛化能力增强。

结论：AdaBoost算法随着弱学习器数目的增加，边界变大，泛化能力增强。

AdaBoost算法的正则化

为了防止AdaBoost过拟合，我们通常也会加入正则化项。AdaBoost的正则化项可以理解为学习率（learning rate）。

AdaBoost的弱学习器迭代：

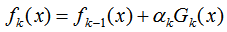
加入正则化项：

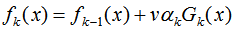
v的取值范围为：0 < v < 1。因此，要达到同样的训练集效果，加入正则化项的弱学习器迭代次数增加，由上节可知，迭代次数增加可以提高模型的泛化能力。

总结

AdaBoost的核心思想在于样本权重的更新和弱分类器权值的生成，样本权重的更新保证了前面的弱分类器重点处理普遍情况，后续的分类器重点处理疑难杂症。最终，弱分类器加权组合保证了前面的弱分类器会有更大的权重，这其实有先抓总体，再抓特例的分而治之思想。

关于AdaBoost算法的过拟合问题，上两节描述当弱学习器迭代数增加时，泛化能力增强。AdaBoost算法不容易出现过拟合问题，但不是绝对的，模型可能会处于过拟合的情况：

（1）弱学习器的复杂度很大，因此选择较小复杂度模型可以避免过拟合问题，如选择决策树桩。adaboost + 决策树 = 提升树模型。

（2）训练数据含有较大的噪声，随着迭代次数的增加，可能出现过拟合情况。