基于动态矩阵方法改进了传统CACC模型预测控制算法

摘要：协同自适应巡航控制(CACC)系统中车辆纵向运动的上下位分层控制器结构，上位控制器采用状态空间模型预测控制算法，利用期望距离以及车辆与环境的实时信息决策出被控车辆运动的期望加速度。下位控制器根据期望加速度，求解发动机节气门开度或制动压力。车辆的执行器时延会对系统的稳定性产生很大的影响。根据动态矩阵控制算法对纯滞后对象的补偿作用，本文提出一种改进的模型预测控制算法，并与PID 控制算法（下位控制器）相结合形成自主车辆纵向运动的上下位分层控制器，以补偿车辆的执行器时延带来的影响。通过 SIMULINK/CARSIM 联合仿真平台对所设计的算法进行了仿真研究，仿真结果表明所设计算法减小了 CACC 系统车辆在跟随过程中的速度跟踪误差以及间距误差，提高了系统的稳定性法。

1.引言

为了解决因汽车保有量增加而带来的社会问题，大量的驾驶员辅助控制系统被深入研究并取得了一定的运用效果[1-2]。比如车道偏离预警系统(lanedeparture warningsystem，LDW)、车道保持辅助系统(land keeping assistance system，LKA)、行人检测和回避系统，交通路口避撞系统和停车辅助系统等。协同自适应巡航控制（CACC）系统以 ACC系统为基础，引入无线通信技术进行车间信息交互并将通信信息用于车辆控制，由此获得比 ACC 系统更好的控制效果，大大提高了自主驾驶的安全性与舒适性[3]。CACC研究主要涉及自适应巡航控制、车间通信技术及控制算法三方面。

2000年，Stankovi等设计了一种基于分布式的重叠控制算法，并对车队的稳定性条件进行相应的分析[4]。2008年，卡内基梅隆大学研究团队构建了油门和制动的非线性 PID控制策略，并设计了基于速度偏差的油门/制动的切换逻辑,进而应用于 Boss 智能车获得了 DARPA挑战赛的冠军[5]。2011年， 郭戈等人对协同驾驶系统进行了分层控制，使系统获得一个较优的控制性能[6]。2012 年，Iftekhar为车辆正常行驶、换道和刹车这三种不同的驾驶状态设定了逻辑切换条件，并设计了协同驾驶控制算法， 从而实现复杂城市道路环境中的协同驾驶[7]。2013年， 以减少燃油损耗为协同控制目标，Stanger重新构建了自主车辆的 MPC优化目标函数[8]。2015 年， Kim 在韩国首尔大学研究室建立了具有集总参数特征的车辆纵向线性模型，进而设计了一种参数时变自适应速度控制器并进行了仿真实验[9]。但是，上述文献忽略了 CACC 车辆执行器的时延，这会降低跟踪的平滑性，甚至使系统发散[10]。

本文首先建立了协同车辆系统的状态空间模型，针对执行器延时，对传统模型预测控制算法(MPC) 进行改进， 以此设计上位控制器。另将CARSIM 中的车辆作为复杂车辆模型以设计下位控制器，二者相结合形成上下位分层结构控制的CACC 系统，并于 CARSIM/SIMULINK 联合仿真平台上进行数值仿真实验。

2.CACC 系统建模

本文采用经典的上下位分层控制结构[11]，上位控制器通过期望距离以及车辆与环境的实时状态信息决策出控制车辆行为的期望加速度；下位控制器根据期望加速度，求解发动机节气门开度和制动压力。

2.1 自主车辆的运动学方程描述

自主车辆纵向运动过程由以下微分方程描述：

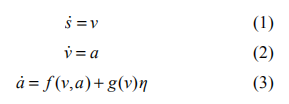
其中 s 为自主车辆相对于惯性参考点的纵向位置， v, a 分别为车辆的速度和加速度，η为发动机的控制输入。函数f 和 g 分别为：

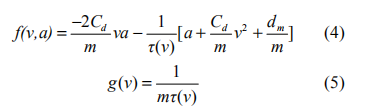
上两式中， Cd 代表了气动阻力系数， m 为车辆的质量， t为车辆发动机的时间常数， dm 为车辆的机械阻力。

将式(4)与(5)中各参数视为先验已知，则可采用下式中的控制律对原非线性模型反馈线性化：

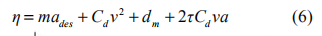
其中 ades 为上位控制器所决定的期望加速度。将式(4)~(6)代入式(3)，可得线性化方程：

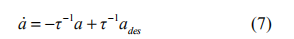
上式也可写为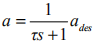，表明发动机跟踪特性可用一阶滞后建模，即实际加速度a 以时间常数τ跟踪期望加速度 ades  。

2.2  CACC车队系统状态空间模型

如图 1，考虑直道上的行驶车队：

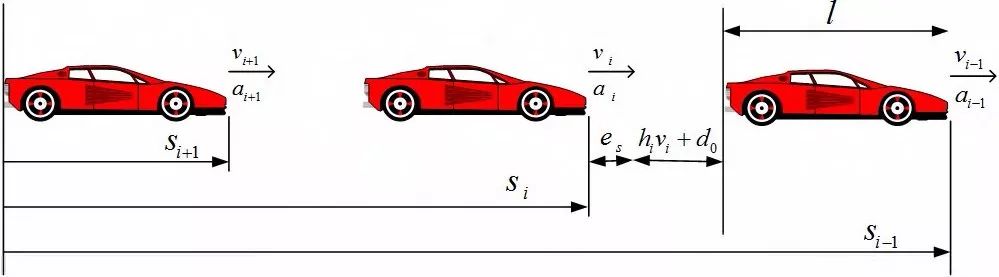
图 1    协同自适应巡航控制车队

其中 si 代表第i 辆车与惯性参考点的距离，vi 、 ai 分别代表第i 辆车的速度和加速度， l 代表车身的长度，则第 i 辆车与前车的车间间距误差为：

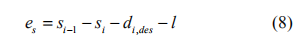
其中 di,des 是第i 辆车距前车的期望车间距离，本文采用固定车头时距策略，有：

其中 d0 表示静止时最小安全距离， h 为常数。此外，定义速度差为：

根据式(2)、(7)~(10)，可以推导出 CACC 系统内车辆的状态空间模型为：

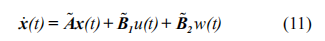
此处

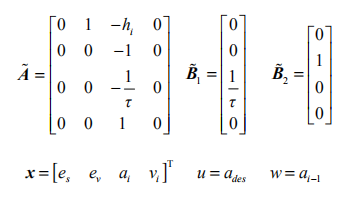
其中x、u和w分别为状态矢量、控制输入以及干扰。

3.上位控制器设计

这部分分析线性状态空间模型中MPC 算法的应用，并在求解有约束的最优化问题时引入松弛变量，在此基础上，针对有执行器时延的系统，提出改进 MPC算法。

3.1 线性状态空间 MPC算法

考虑以下离散状态空间模型：

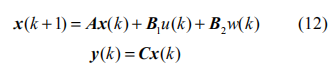
其中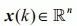表示系统状态向量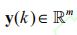，表示系统输出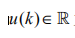，为系统控制输入，而 w(k) 为前车加速度， C = [1, 0, 0, 0; 0,1, 0, 0] 为输出矩阵。

假设每个采样周期ts的状态和干扰可测，通过迭代计算，记 x(k + j | k) 为系统在 k 时刻对 k + j 时刻的状态预测，以u(k |k) 代表预测的控制输入，控制过程通过增量控制Δu 实现：

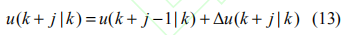
则可得到总的模型预测状态方程为：

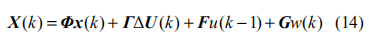
其中参数矩阵Φ,Γ,F,G 见[12]，k时刻的预测控制输出为：

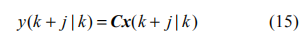
定义性能指标函数:

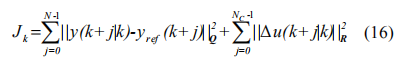
其中 yref 为参考轨迹，N 为预测时域，NC 为控制时域。Q, R 分别为误差和输入加权矩阵。

优化函数的向量形式为：

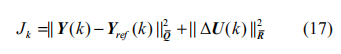
其中

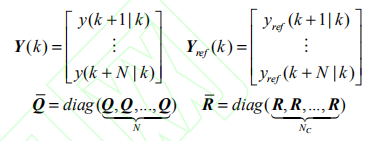
定义向量 E(k) 为系统自由响应与未来目标轨迹的偏差：

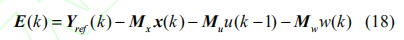
其中

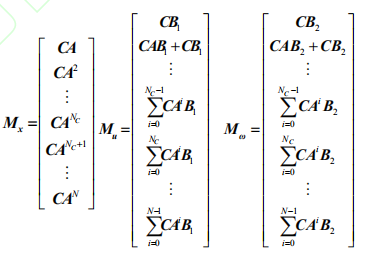
将(18)式代入(17)可得：

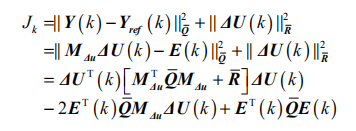
上式可被写为二次规划的标准形式：

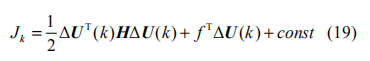
其中

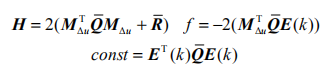
其中， MΔu 为 Γ 中每个分块矩阵左乘C 。

假设优化函数受到如下的逐点约束条件：

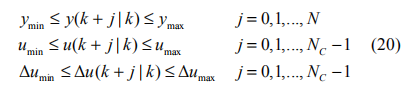
上式对应的向量形式为：

其中

I 为 P 维单位矩阵，其中参数矩阵ΔUmax ,ΔUmin ,Umax,U min  见[11]，Π 为 PNC 维单位矩阵。

3.2 引入松弛变量

求解有约束最优化问题时，过于严格的约束可能得不到可行解，需引入松弛变量作为罚函数加入原目标函数，得到新的优化函数：

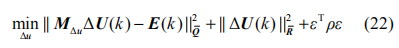
此处 ε 为松弛变量而 ρ 为其权重。新的约束条件为：

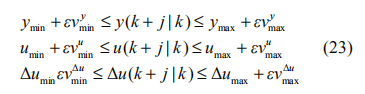
3.3 考虑执行器延时的改进 MPC 算法

由于Δu (k ) 是极小化性能指标得到的解，则必须满足极值必要条件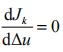 ，可得式(22)的解：

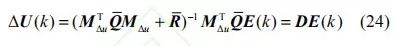
k 时刻的实际增量控制输入为：

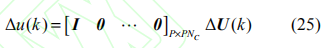
对执行器时延系统，基于动态矩阵控制思想改进传统 MPC 算法。将增量控制输入视为阶跃输入，则执行器时延对应系统阶跃响应系数的时延，进而转换为控制输入的时延。故执行器时延为θ 的系统相当于具有纯滞后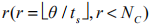拍的离散模型其增量控制输入表示为：

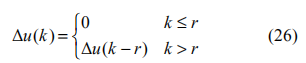
对应的优化参数变为：

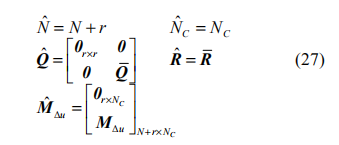
由改进算法求得的控制输入为:

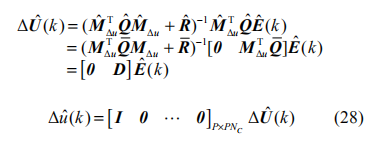
以上分析说明，对于执行器时延系统，在传统MPC 控制器基础上，将参数按式(27)进行修改，并以Δu(k-r) 作为 k 时刻的增量控制输入即可。

4.下位控制器设计

实际车辆在行驶的过程中，加速控制和制动控制分开执行，可根据期望加速度大小进行逻辑切换，当 ades ≥ 0 时，采用加速控制，当 ades<0  时，采用制动控制。

4.1 逆动力学模型

图 2 为不同油门开度下发动机转速与扭矩的关系曲线，其中每条曲线旁边的数字对应油门开度。

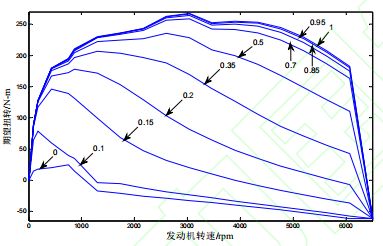
图 2 逆动力学发动机扭矩特性曲线

若已知发动机转速 we 和期望扭矩Te,des ，便可通过查表法得到对应的期望油门开度αdes ，即：

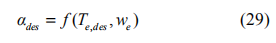
4.2 加速控制

自主车辆纵向行驶是汽车牵引力、风阻力与地面阻力共同作用的结果，行驶状态与车辆的具体模型、道路的光滑程度以及风阻力系数的大小等息息相关。纵向行驶过程中的等效空气阻力为：

其中  ρa 为空气质量密度，Cd 为空气阻力系数，AF 为车辆的正面迎风面积，Vx 和Vwind 分别为车辆的纵向速度以及风速。

空气阻力 Faero 是车辆速度的二次函数，可表示为发动机转速 we 的二次函数： 

由式(30),有

Rp 为车轮转速 ww 与发动机转速 we 之间的比值，即变速齿轮比。 reff  为轮胎有效半径。

加速过程中，发动机期望扭矩Te des , 与期望加速度之间的关系为：

式中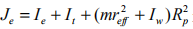是反映在发动机侧的有效转动惯量， Ie 为发动机转动惯量，m 为汽车质量。Rx 为所有滚动阻力之和，与滚动阻尼系数 f 有关，因为 f 一般取值为0.01-0.04，故 Rx 值很小，本文予以忽略。由于

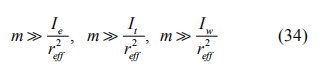
则Je 可改写为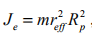，式(32)重写为：

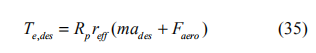
本文研究对象为前轮驱动式的 B 型掀背式轿车，由逆动力学关系得到相应的期望油门开度αdes ,采用 PID 算法对误差进行校正，最终油门输入为：

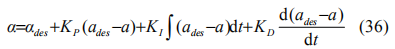
测试后设定参数为。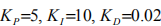

4.3 制动控制

汽车制动时，根据期望加速度求出期望制动压力。制动过程时车辆动力学方程为：

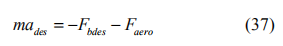
在制动力不超过路面所能达到的最大制动力的情况下，可以将制动力 Fbdes 与制动压力 Pbdes 视为线性关系：

CARSIM 仿真可得  Kb = 1286.174。

由式(36)与式(37)可得期望制动压力为：

采用与加速控制时相同的 PID 控制器进行校正，得到最终的制动压力为：

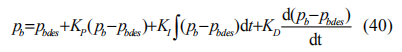
5.CARSIM/SIMULINK 联合仿真

CARSIM 提供了与 SIMULINK 联合仿真的接口，通过 S 函数实现通信。联合仿真实验采用的CARSIM 车辆均为前轮驱动式的 B 型轿车，发动机功率为 125kW，仿真环境为长 1200m 的单行道。车辆在 CARSIM 中设置为“AT 4th Mode”运动模式，即车辆自动驾驶在 4 档及 4 档以下，根据发动机转速自动选择传动比。自动切换转速曲线如图 3 所示：

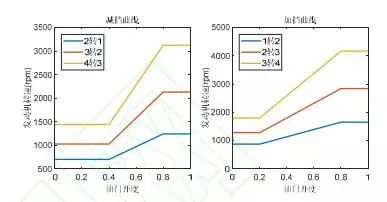
图 3 加减档下油门门开度与发动机转速曲线

车辆运行在 1 档时传动比为 0.28,在 2 档时0.485, 在 3 档时 0.71,在 4 档时为 1.00。

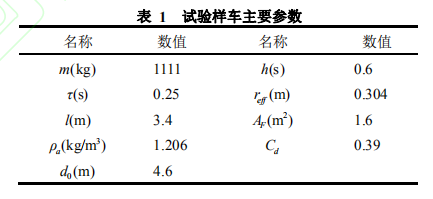
实验样车各参数如表 1 所示：

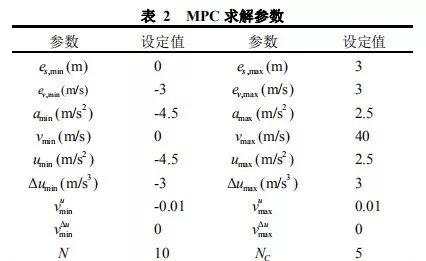
约束参数、松弛变量和控制器优化参数设为：

联合仿真模型如下：

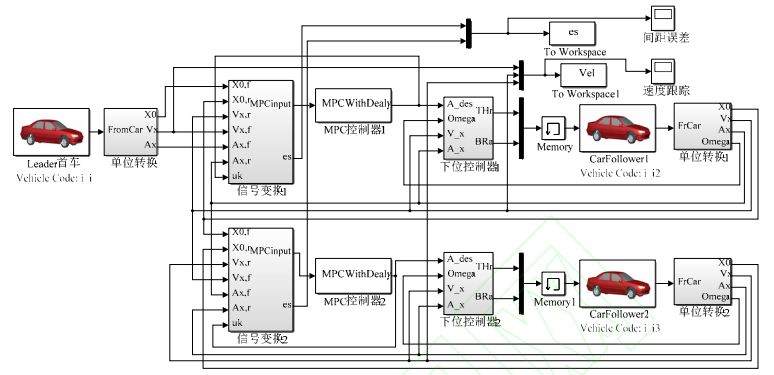
图 4 上下分层控制系统仿真模型

执行器延时为 0.2s，采样周期 0.1s，基于上下位分层控制的 CACC 系统进行建模仿真。三辆车的初始位置分别为 20m、12m 和 4m，初始速度与加

速度都为 0。首车速度曲线如图 5 a)中的 V1所示。

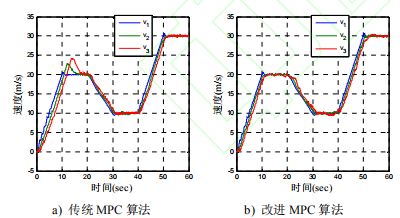
图 5 两种算法下 CACC 系统车辆的速度曲线

由图 5 可知，采用传统 MPC 算法的自主车辆虽然能跟踪上前车的速度，但跟踪过程中出现超速和较大抖动，可能导致车队的不稳定。而采用改进MPC 算法时后面车辆没有超速行为，跟踪曲线相对平滑，队列运行稳定，验证了改进算法的有效性。

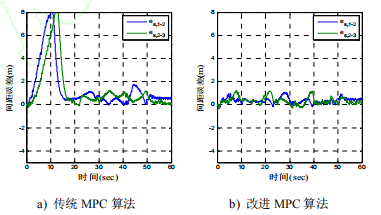
图 6 两种算法下 CACC 系统车辆间间距误差

图 6 中 ,es,1-2，es2-3分别代表首车与第二辆车，第二辆车与第三辆车之间的间距误差。对比可知，传统 MPC 算法下车辆间距超过了约束限制，间距过长会导致无法保持紧密队形，违背 CACC 系统保持较小间距以增大道路交通容量的设计初衷。改进MPC 算法可将车辆间距误差保持在 1.5m 以内，是传统方法的 18.7%，验证了改进算法的有效性。

当执行器时延为 0.4s 时，车辆跟踪性能下降，第二辆车和首车的最大间距误差达到 2.5m，第三辆车与第二辆车的间距误差则最高达到 3.96m，相比时延为 0.2s 时变差；时延为 0.4s 时传统 MPC 算法无法保证系统的稳定性。执行器时延为 0.1s 时，速度跟踪比较平滑，间距误差也控制在 1.2m 以内。改进后的算法在执行器时延存在的情况下仍能实现车辆跟踪，但随着时延增大，系统性能指标有所下降。

6.结束语

本文针对车辆的执行器时延，基于动态矩阵方法改进了传统 CACC 模型预测控制算法。在每个采样时刻，上位控制器将控制量求解问题转化为一个二次型优化问题，得到车辆期望加速度，再根据车辆逆纵向动力学模型设计 PID 下位控制器，二者相结合组成分层控制结构，实现对复杂车辆模型的协同控制。CARSIM/SIMULINK 联合仿真验证了改进算法有效性。