使用COMSOL模拟量子力学中的隧穿现象

在经典力学中，当粒子携带的能量不足以克服势垒时，粒子是无法穿过势垒的。但是在量子力学中，电荷等微观粒子却能够穿越大于其自身携带总能量的势垒层，这就是量子隧穿效应。我们可以使用 COMSOL® 软件的“半导体模块”中提供的 WKB 隧穿模型来以及异质结和肖特基等边界条件，描述量子隧穿的相关现象。在下文中，我们将通过基准模型演示其用法。

Wentzel-Kramers-Brillouin 近似

根据 K.Yang、J.R.East 和 G.I. Haddad 的参考文献（Ref. 1），若采用 Wentzel-Kramers-Brillouin（WKB）近似假设，隧穿电流会向热离子电流增加一个分数因子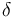

(1)

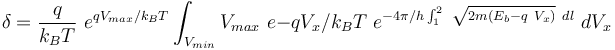
其中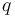

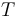
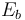
内积分

WKB 隧穿模型

为了使用 WKB 近似模拟隧穿效应，首先需要设置边界条件，此步骤涉及添加隧穿产生的额外电流密度。针对异质结，选择热电子发射；针对金属接触，选择理想肖特基。选定上述（非默认）选项之后，新建的额外电流贡献 栏将立即显示在界面中，我们即可为电子和空穴分别指定额外电流贡献。默认情况下，不需要添加额外电流。我们还可以在内置的 WKB 隧穿模型和用户定义选项间进行选择。请参考下方示例截图。

选择热电子发射以添加额外电流贡献。

如上文所述，对于与势垒相关的变量，电子和空穴的计算方式不同，所以我们为每种类型的载流子引入了不同的特征，它们在“模型开发器”中被添加到异质结或肖特基接触边界条件的子节点。请参考下方示例截图。

“模型开发器”的树结构和 WKB 隧穿模型，电子 特征的设置窗口。

在上图的设置 窗口中，边界选择 通常指定添加了额外电流密度的边界。域选择则指定势垒所在的相邻域。第二个边界选择指定了与第一个边界选择相对的域的边界。隧穿基本发生在选定域内，即第一个和第二个边界选择之间。

在二维和三维模型中，除了有效质量之外，我们还需要输入一个描述电场线方向的坐标变量，并输入一个（二维）或两个（三维）跨过隧穿边界的坐标变量。在简单的矩形几何中，内置空间变量x，y和z（或基于它们的表达式）可用于定义坐标变量。在更通用的几何中，则可以使用曲线坐标 数学接口。“案例下载”中的“异质结隧穿”教学模型演示了后一种方法。

渐变异质结模型

异质结隧穿模型比较了在不同温度下，发生与不发生隧穿效应的渐变异质结的电流密度模拟值。为了便于比较仿真结果，设备构型和所有材料属性均来源于参考文献（特别是 3.3 节）。

这是一个分子束外延生长的 AlxGa1-xAs 渐变异质结，它形成了可阻挡电子的三角形势垒。为了获得与实验数据的最佳拟合，文献作者在运行每个仿真时使用了一组未必与实验标称值相同的材料及设备参数。为了方便比较仿真结果，我们采用了作者选定的一组模拟参数，理由与文献提出的论点一致。

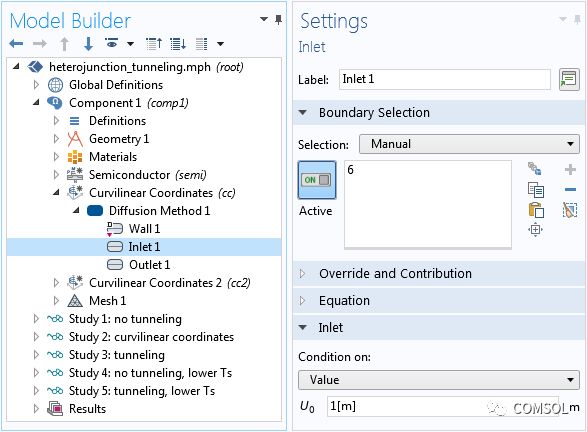
我们通过在空间上改变 AlxGa1-xAs 层中铝的摩尔分数来形成三角形势垒层。在 COMSOL Multiphysics® 软件中，我们能够基于摩尔分数等局部变量，以及参考温度、晶格温度和掺杂浓度等参数和变量，直接创建材料并定义材料属性。摩尔分数则通过空间变化变量来定义。使变量在空间中变化有两种方法：使用显式表达式，或者在不同域内使用不同定义。我们在模型中利用了这两种方法。如下方截图所示，我们在定义下创建了多个变量节点，在不同域内应用不同的掺杂变量和摩尔分数。此外，我们利用内置的空间坐标变量 x 使摩尔分数在“域 2”内具有空间依赖性。

通过在 定义下添加多个节点（每个域对应一个节点），对不同的域应用不同的掺杂与摩尔分数变量。内置变量 x 使变量Al_frac具有空间依赖性。

上文所定义的空间依赖性变量可以用在材料与物理场的定义中，如下图所示。

我们将掺杂变量N_D直接输入到掺杂特征中，如下方截图所示。

在掺杂浓度的定义中使用空间因变量N_D。

我们利用摩尔分数变量Al_frac在材料定义中定义了一个便捷符号 x，此符号位于基本子节点的设置窗口的局部属性栏中，并被用于定义态密度（DOS）有效质量、相对介电常数、带隙、电子亲和性和迁移率。请注意，利用前缀 def，我们可以访问定义在基本 子节点中、带def标签的符号。例如，在下方截图中，输入框中的表达式def.x可用于访问有效质量me和mh。

通过符号def.x使用材料定义中的空间因变量 Al_frac。

当访问物理场设置中的材料属性时，可以利用前缀material。以下方的截图为例，它利用表达式material.def.x来查找符号x。前文截图显示另一个示例，它利用表达式 material.def.me访问电子有效质量。

使用前缀material访问物理场设置中的材料属性。

建立曲线坐标

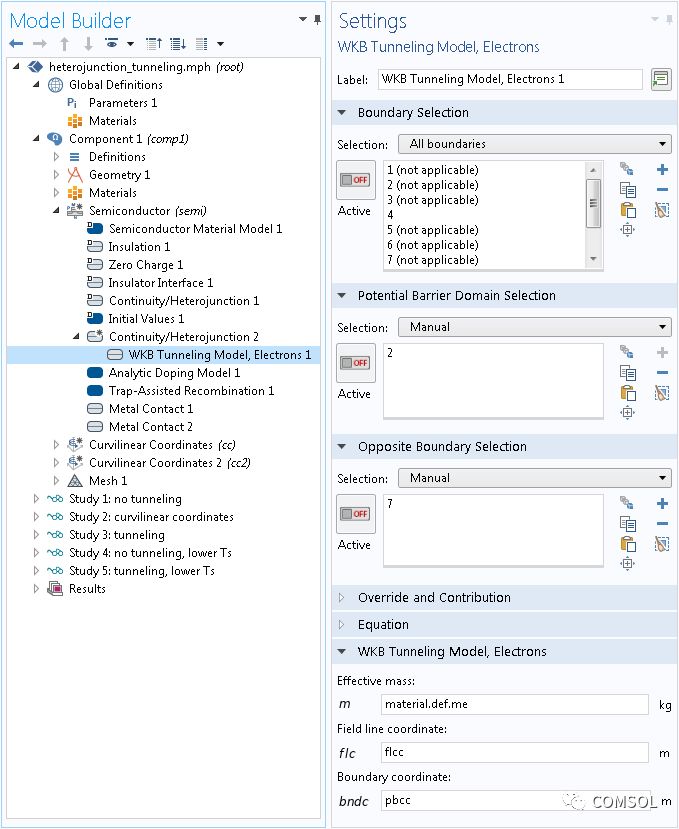
如前文所述，（在通用几何的内置变量x、y和  z的简单表达式不可行的情况下）我们可以利用曲线坐标 接口沿电场线与隧穿边界建立坐标。此模型几何是一个简单的矩形（见 Ref. 1 中的图 2b），电场线和隧穿边界坐标简单地表示为 x 和 y。不过为了进行演示，我们仍然在此模型中使用曲线坐标 接口。如下方截图所示，我们在“模型开发器”中创建了两个包含扩散方法 选项的曲线坐标 接口，一个用于电场线，另一个用于隧穿边界。

入口边界的设置窗口。

将入口和出口边界置于在势垒域的另一侧，这样可以使解沿期望坐标发生变化。两个曲线坐标接口的解如下图所示。

两个曲线坐标 接口的解。垂直等值线是电场线的坐标，水平等值线是隧穿边界的坐标。

在此示例中，域 2 恰好覆盖了感兴趣区域，顺势对势垒进行线积分。通常情况下，我们可以使用几何内的不同边界来定义感兴趣区域，这些边界可能与材料边界重合，也可能不重合。

对于任意几何，曲线坐标 接口的解也许与电场线坐标不完全重合。不过，它为我们提供了良好的近似，并省去了通过数值方式搜索场线的麻烦。

上图中的解可用于定义 WKB 隧穿特征的坐标变量。下方截图显示了变量定义，前文截图显示了 WKB 特征的设置。

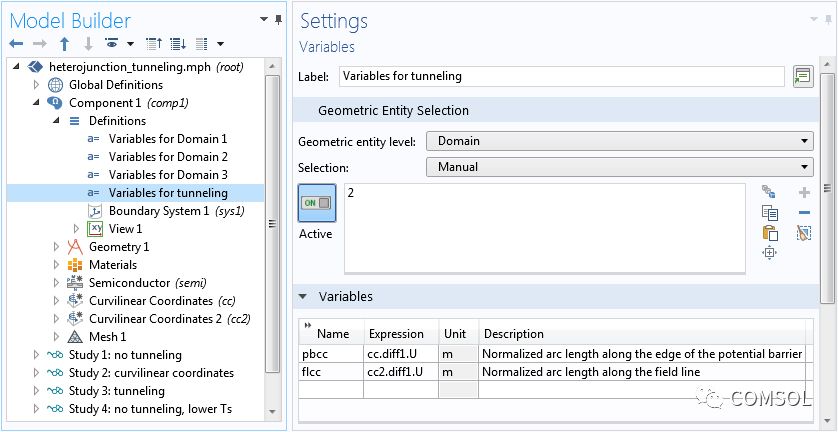
设置窗口显示隧穿变量的定义。

模拟隧穿效应的其他物理场设置

由于隧穿效应对势垒的形状高度敏感，所以我们改用有限元准费米能级公式。考虑到因变量在每个网格单元内均为常数，所以缺省的有限体积公式需要更加精细的网格。

我们在模型树中建立两个异质结边界条件，借此计算与比较包含与不包含隧穿效应的结果。

求解渐变异质结模型

该模型分阶段进行求解。“研究 1”计算了无隧穿效应的情况。因为曲线坐标在整个模型中不变，所以“研究 2”仅进行一次求解。

“研究 3”求解了包含隧穿效应的情况，而且只包含半导体物理场。为了提供良好的初始条件，我们使求解变量的初始值 指向“研究 1”的解。由于隧穿特征所需的曲线坐标 接口未包含在研究步骤中，所以我们使不求解的变量值 指向“研究 2”中的解，从而对曲线坐标进行定义。下方截图显示了相关设置。

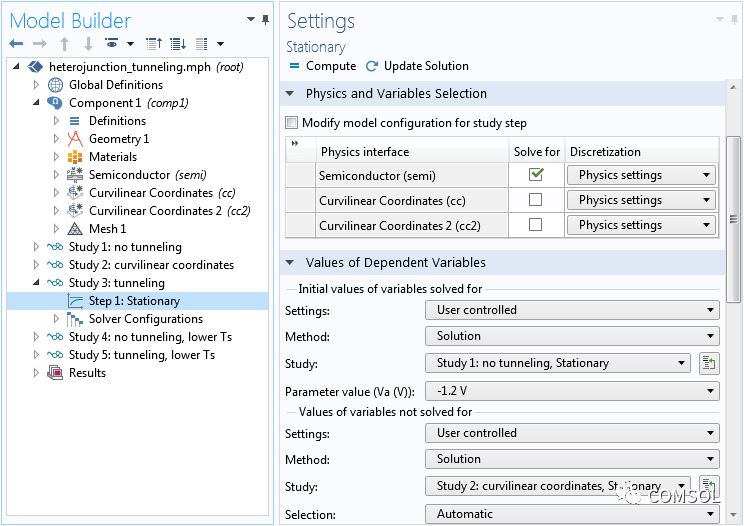
研究设置。注意求解变量的初始值和不求解的变量值使用了不同的研究。

另外两项研究采用了相似的求解变量的初始值 和不求解的变量值 设置，主要计算低温下的情况。对于非线性方程系统，我们需要为辅助扫描建立一个良好的初始条件。我们发现，在温度较低的情况下，如果对 I-V 曲线从低电压扫描到高电压，收敛会更加容易。

比较仿真结果与参考文献

下图比较了温度为 300 K 时，有无隧穿效应分别对应的电流密度与电压（J-V）曲线。结果与 Ref. 1 中的图 12 很好地吻合。

比较有和没有隧穿效应情况下的 J-V 曲线。

为了解释势垒宽度对隧穿电流大小的影响，文献图 13 比较了两个偏置电压下的导带结构示意图和电子准费米能级。我们的模型准确地还原了相关数据，如下所示。

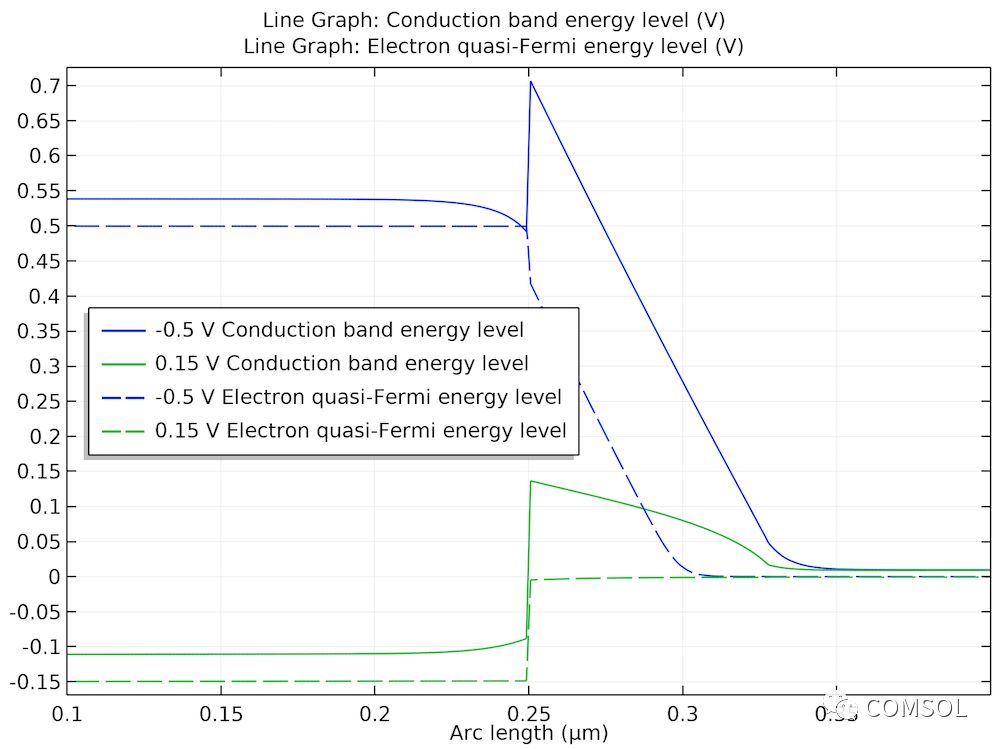
两个偏置电压下的导带图说明了势垒宽度对隧穿效应产生的影响。

最后，下图表明不同温度下的 J-V 模拟曲线与文献的图 14 基本一致。

不同温度下的 J-V 曲线。

结语

在本篇博客文章中，我们利用渐变异质结基准模型演示了 WKB 特征，并介绍了如何创建用户定义的三元材料属性。我们讨论了在研究设置中定义求解变量的初始值 和不求解的变量值 的基本技巧，这些技巧可应用于很多建模情景。我们希望您会将这些功能与技巧应用到仿真工作中。

如希望亲手尝试“异质结隧穿”模型，请单击下方按钮跳转至“案例下载”页面。登录 COMSOL Access 帐户后，您可以下载此示例的文档，如果您拥有有效的软件许可证，还可以下载 MPH 文件。