如何创造可信任的机器学习模型？先要理解不确定性

来源：机器之心编译 作者：Eric Jang

不确定性是机器学习领域内一个重要的研究主题，Eric Jang近日的一篇博客对这一主题进行了详细的阐述。顺便一提，他的博客还有一些有趣的深度学习迷因。

在谈到人工智能安全、风险管理、投资组合优化、科学测量和保险时，人们都会提到「不确定性（uncertainty）」的概念。下面有几个人们言语中涉及不确定性的例子：

「我们想让机器学习模型知道它们不知道的东西。」

「负责诊断病人和给出治疗方案的AI应该告诉我们它对自己的推荐的信心。」

「科学计算中的显著性值代表了测量中的不确定性。」

「我们想让自动智能体探索它们不确定（对于奖励或预测）的区域，这样它们也许能发现稀疏的奖励。」

「在投资组合优化中，我们希望最大化回报，同时限制风险。」

「由于地缘政治不确定性增大，美国股市2018年在失望中收尾。」

那「不确定性」究竟是什么？

不确定性度量反映的是一个随机变量的离散程度（dispersion）。换句话说，这是一个标量，反应了一个随机变量有多「随机」。在金融领域，这通常被称为「风险」。

不确定性不是某种单一形式，因为衡量离散程度的方法有很多：标准差、方差、风险值（VaR）和熵都是合适的度量。但是，要记住一点：单个标量数值不能描绘「随机性」的整体图景，因为这需要传递整个随机变量本身才行！

尽管如此，为了优化和比较，将随机性压缩成单个数值仍然是有用的。总之要记住，「越高的不确定性」往往被视为「更糟糕」（除了在模拟强化学习实验中）。

不确定性的类型

统计机器学习关注的是模型p(θ|D)的估计，进而又估计的是未知随机变量p(y|x)。其中有多种不同形式的不确定性。某些不确定性的概念描述了我们能够预期的固有的随机性（比如抛硬币的结果），另一些概念则描述了我们对模型参数的最佳猜测的信心缺乏程度。

为了说得具体一点，我们假设有一个循环神经网络（RNN）需要根据一个每日气压表读数序列预测当天的降雨量。气压表能检测大气压，大气压下降往往是降雨的前兆。下图总结了降雨量预测模型与不同类型的不确定性。

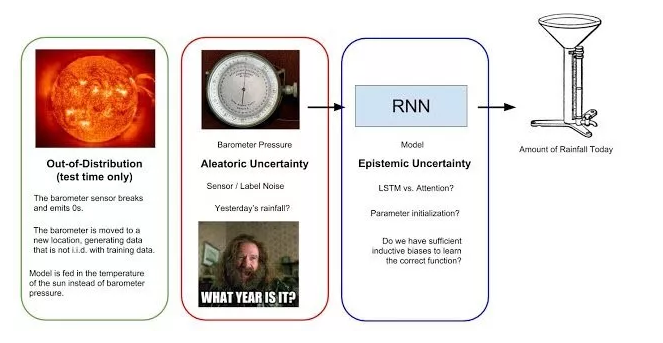
图1：试图根据气压表读数序列预测每日降雨量的简单机器学习模型可能考虑的不确定性。偶然事件不确定性（AleatoricUncertainty）源自数据收集过程，是不可降低的随机性。认知不确定性（EpistemicUncertainty）反映的是模型做出正确预测的置信程度。最后，超出分布的误差（Out-of-Distributionerror）是指当模型的输入不同于其训练数据时出现的不确定性（比如太阳温度等其它异常现象）。

偶然事件不确定性

偶然事件不确定性得名于拉丁语词根aleatorius，意为「将几率纳入创造过程」。这描述的是源自数据生成过程本身的随机性；不能简单地通过收集更多数据而消除的噪声。就像你不能预知结果的抛硬币。

在降雨量预测的类比中，偶然事件不确定性源自气压表的不准确度。也还存在这种数据收集方法没有观察的重要变量：昨日的降雨量是多少？我们测量大气压的时代是现代还是上个冰河时代？这些未知是我们的数据收集方法中固有的，所以用该系统收集更多数据无法帮助我们消除这一不确定性。

偶然事件不确定性会从输入传播到模型的预测结果。假设有一个简单模型y=5x，它的输入取自正态分布x～N(0,1)。在这一案例中，y～N(0,5)，因此该预测分布的偶然事件不确定性可描述为σ=5。当然，当输入数据x的随机结构未知时，预测结果的偶然事件不确定性将更难估计。

也许有人会想：因为偶然事件不确定性是不可约减的，所以我们对此无能无力，直接忽略它就好了。这可不行！在训练模型时，应该注意选择能够正确地代表偶然事件不确定性的输出表征。标准的LSTM不会得出概率分布，所以学习抛硬币的结果时只会收敛成均值。相对而言，用于语言生成的模型能够得出一系列类别分布（词或字符），这能纳入句子完成任务中的固有歧义性。

认知不确定性

「好的模型都是相似的；差的模型各有不同。」

认知不确定性来自希腊语词根epistēmē，属于与知识相关的知识。这衡量了我们对「源自我们对正确模型参数的无知程度」的正确预测的无知程度。

下图展示了一个在某个简单的一维数据集上的高斯过程回归模型。其置信区间反映了认知不确定性；训练数据的认知不确定性为零（红点）。随着我们离训练数据点的距离越远，模型应该给预测分布分配越高的标准差。不同于偶然事件不确定性，认知不确定性可以通过收集更多数据和「去除」模型缺乏知识的输入区域而降低。

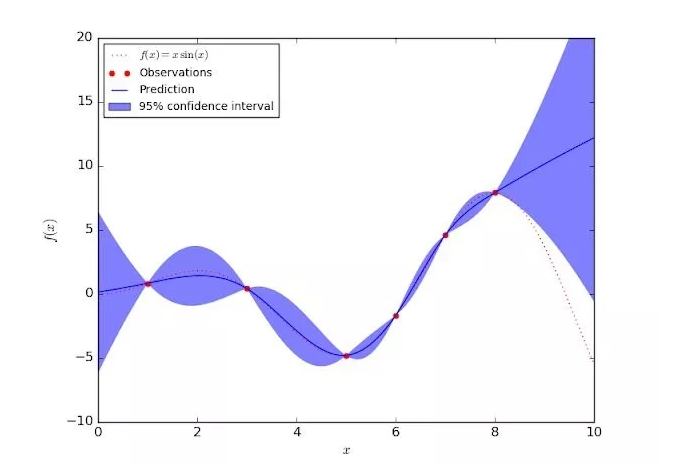
图2：一维高斯过程回归模型，展现了训练集之外的输入上的认知不确定性

深度学习与高斯过程之间有丰富的关联。人们希望能通过神经网络的表征能力扩展高斯过程的能感知不确定性的性质。不幸的是，高斯过程难以扩展用于大数据集的统一随机小批量设置，而且研究大型模型和数据集的人也已经不再支持这种方法。

如果人们希望在选择模型族时有最大的灵活度，使用集成（ensemble）方法来估计不确定性是一个好选择，这实际上就是使用「多个独立的学习后的模型」。高斯过程模型是分析式地定义预测分布，而集成方法则被用于计算预测的经验分布（empiricaldistribution）。

由于训练过程中出现的随机化偏差，任何单个模型都会有一些误差。在集成方法中，其它模型往往会揭示出单个模型特有的错处之处，同时认同推理正确的预测结果；因此集成模型是很强大的。

我们该如何随机取样模型以构建一个集成模型呢？在使用bootstrapaggregation构建集成模型时，我们首先从一个大小为N的训练数据集开始，并从原始训练集采样M个大小为N的数据（有替换，这样每个数据集都不会占据整个数据集）。分别在这些数据集上训练M个模型，再将它们的预测结果综合起来得到一个经验预测分布。

如果训练多个模型的成本过高，也可以使用dropout训练来近似模型集成。但是，引入dropout会涉及到一个额外的超参数并且也可能有损单个模型的表现（对于实际应用而言往往是不可接受的；在实际应用中，校准不确定性估计相对准确度而言是次要的）。

因此，如果能使用大量计算资源（就像谷歌那样），通常只需要重复训练多个模型副本，这要更加容易。这还能在无损性能的前提下享受集成方法的好处。这篇深度集成论文就采用了这一方法：https://arxiv.org/pdf/1612.01474.pdf。这篇论文的作者还提到由不同的权重初始化带来的随机训练动态足以得到一个多样化的模型集合，而不必通过bootstrapaggregation来降低训练集多样性。从实际的工程开发角度看，押注不会影响模型性能的风险估计方法或研究者想要尝试的其它方法是明智的

超出分布的不确定性

对于我们的降雨量预测器，如果我们为其提供的输入不是气压表读数序列，而是太阳的温度呢？要是提供一个全是零的序列呢？或者用不同的单位记录的气压表读数呢？RNN还是会继续计算，为我们提供一个预测，但结果很可能毫无意义。

这个模型完全没有能力基于通过不同于训练集创建流程的流程生成的数据进行预测。在基准驱动的机器学习研究领域，这是一种常被忽视的失败模式，因为我们通常假设训练、验证和测试集都完全由独立同分布的数据构成。

确定输入是否「有效」是实际部署机器学习所面临的一个严峻问题，这也被称为超出分布（OoD/OutofDistribution）问题。OoD与「模型误设错误」和「异常检测」是同义词。

异常检测不仅对增强机器学习系统稳健性很重要，而且本身也是一种非常有用的技术。举个例子，我们可能想构建一个能监控健康人士的生命体征的系统，让该系统能在指标异常时发出警报，这并不需要系统之前见过这种异常的病理模式。我们也可以用异常检测来管理数据中心的「健康」，一旦有不同寻常的事情发生（磁盘满载、安全漏洞、硬件故障等），我们就能得到通知。

因为OoD输入仅出现在测试时间，所以我们不应假设我们事先知道模型会遇到的异常的分布。这正是OoD检测的棘手之处——我们必须针对模型在训练阶段从未见过的输入来增强该模型对这些输入的抗性！这正是对抗式机器学习中描述的标准的攻击场景。

机器学习模型有两种处理OoD输入的方法：1）在输入到达模型前就识别出糟糕的输入；2）根据模型预测结果的「怪异性」来帮助我们鉴别可能存在问题的输入。

在第一种方法中，我们不会对下游机器学习任务做任何假设，只会考虑输入是否处于训练分布中的问题。这正是生成对抗网络（GAN）中判别器的工作。但是，单个判别器并不具有完美的稳健性，因为它只擅长辨别真实数据分布和生成器得到的分布；对于不属于其中任意一个分布的输入而言，它有可能得出任意的预测结果。

除了判别器，我们也可以构建一个分布内数据的密度模型，比如一个核密度估计器或用一个NormalizingFlow来拟合数据。HyunsunChoi和我最近研究过这一问题，参阅我们最近使用现代生成模型执行OoD检测的论文：https://arxiv.org/abs/1810.01392

第二种OoD检测方法涉及到使用任务模型的预测（认知）不确定性来辨别哪些输入是OoD。理想情况下，模型在收到错误的输入时应该会得到「怪异的」的预测分布p(y|x)。举个例子，HendrycksandGimpel（https://arxiv.org/abs/1610.02136）表明OoD输入的最大化softmax概率（预测得到的类别）往往低于分布内的输入。这里，不确定性反比于最大softmax概率建模的「置信度」。高斯过程这样的模型能通过构造为我们提供这些不确定性估计，或者我们也可通过深度集成来计算认知不确定性。

在强化学习领域，人们实际上假设OoD输入是一件好事，因为这是智能体还不知道如何处理的世界输入。鼓励策略寻找自己的OoD输入能实现「内在的好奇心」，从而探索模型的预测效果较差的区域。这是很好的做法，但我很好奇如果将这种好奇心驱动的智能体部署到现实世界（其中传感器很容易损坏，也会发生其它实验异常）中会怎样。机器人如何区分「未曾见过的状态」（好）和「传感器损坏情况」（坏）？这能得到能学习与它们的传感机制交互从而生成最大化新颖度的智能体吗？

谁来看住看门狗？

正如前一节提到的那样，保护自己免受OoD输入影响的一种方法是设置一个能够「像看门狗一样」监控模型输入的似然模型（likelihoodmodel）。我更喜欢这种方法，因为这能将OoD输入问题与任务模型中的认知和偶然事件不确定性隔开。从工程开发角度看，这能让分析工作更轻松。

但我们不应该忘记这个似然模型也是一个函数近似器，可能存在自己的OoD错误！我们近期的生成式集成方法（GenerativeEnsembles，https://arxiv.org/abs/1810.01392，也可参阅DeepMind的同期研究https://arxiv.org/abs/1810.09136）研究表明，在使用一个CIFAR似然模型时，来自SVHN的自然图像实际上比CIFAR分布内的图像本身还有更高的可能性！

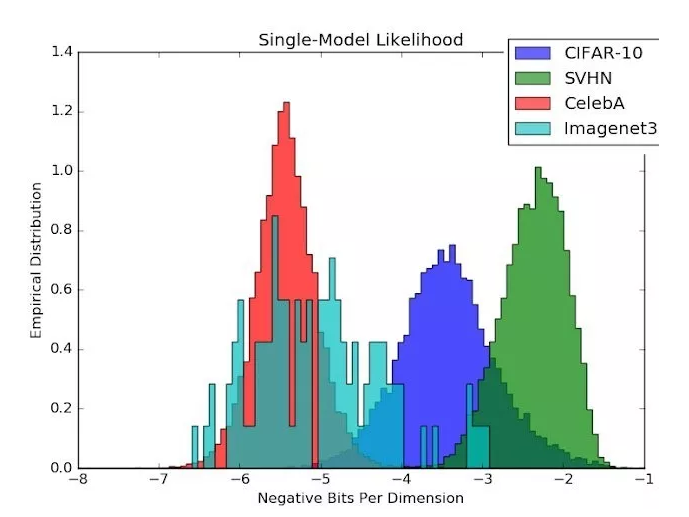
图3：似然估计涉及到一个本身也可能易受OoD输入影响的函数近似器。比起CIFAR测试图像，CIFAR的似然模型会给SVHN图像分配更高的概率！

但是，希望还是有的！研究表明，似然模型的认知不确定性对该似然模型自身而言是出色的OoD检测器。通过将认知不确定性估计与密度估计结合起来，我们能以一种与模型无关的方式使用似然模型的集成来保护机器学习模型免受OoD输入影响。

校准：下一件大事？

警告：只是因为一个模型能够确定一个预测结果的置信区间，并不意味着该置信区间能真正反映结果在现实中的实际概率！

置信区间（比如2σ）隐式地假设预测分布是高斯分布，但如果你想要预测的分布是多模态分布或重尾分布，那么你的模型将不会得到很好的校准！

假设我们的降雨量预测RNN告诉我们今日的降雨将为N(4,1)英寸，如果我们的模型经过校准，那么如果我们一次又一次地在同样的条件下重复这个实验（也许每一次都重新训练该模型），那么我们实际将会观察到实际的降雨量分布正是N(4,1)。

当今学术界开发的机器学习模型大都是针对测试准确度或某个拟合度函数优化的。研究者执行模型选择的方式不是通过重复相同的实验来部署模型，再衡量校准误差，所以不出意外，我们的模型往往只有很差的校准，参阅：https://arxiv.org/abs/1706.04599

展望未来，如果我们要信任部署在现实世界中的机器学习系统（机器人、医疗系统等），我认为「证明我们的模型能够正确理解世界」的一种远远更为强大方法是针对统计校准测试它们。优良的校准也意味着优良的准确度，所以这是一个更严格的更高的优化指标。

不确定性应该是标量吗？

尽管标量的不确定性很有用，但它们的信息量永远不及它们所描述的随机变量，我发现粒子滤波和分布式强化学习等方法非常酷，因为它们是在整个分布上运行的算法，让我们无需借助简单的正态分布来跟踪不确定性。除了使用单标量的「不确定性」来塑造基于机器学习的决策，现在我们也可以在决定要做什么时查询分布的整体结构。

Dabneyetal.的ImplicitQuantileNetworks论文（https://arxiv.org/pdf/1806.06923.pdf）很好地讨论了如何基于回报的分布构建「风险敏感型智能体」。在某些环境中，人们可能更偏好倾向于探索未知的机会主义策略；而在另一些环境中，未知事物可能并不安全，应当避开。风险度量的选择本质上决定了如何将回报的分布映射成一个标量数量，然后再根据这个量进行优化。所有的风险度量都可以根据分布计算得到，所以预测整个分布能让我们将多个风险定义轻松地组合起来。此外，支持灵活的预测分布似乎也是一个提升模型校准的好方法。

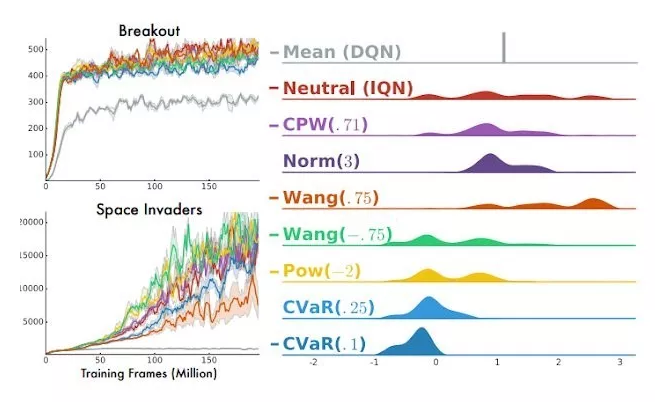
图4：多种风险度量在Atari游戏上的表现，来自这篇IQN论文：https://arxiv.org/abs/1806.06923

对金融资产管理者而言，风险度量是一个非常重要的研究主题。简单纯粹的马科维茨（Markowitz）投资组合的目标是最小化投资组合回报的一个加权的方差。但是，方差是「风险」在金融语境的一个不直观的选择：大多数投资者根本不在乎回报超出预期，而只是希望最小化回报少或亏损的可能性。由于这个原因，Value-at-Risk、ShortfallProbability和TargetSemivariance等仅关注「糟糕」结果的概率的风险度量是更有用的优化目标。

不幸的是，它们也更难分析。我希望在分布式强化学习、蒙特卡洛方法和灵活的生成模型上的研究能让我们构建起能与投资组合优化器很好地协同工作的风险度量的可微分弛豫（differentiablerelaxations）。如果你在金融行业工作，我强烈建议你阅读IQN论文中的「强化学习中的风险」一节。

总结

下面总结了本文的一些要点：

不确定性/风险度量是「随机性」的标量度量。为了优化和数学计算的方便，将随机变量浓缩成了单个数值。

预测不确定性可以分解成偶然事件不确定性（来自数据收集过程的不可约减的噪声）、认知不确定性（对真实模型的无知）和超出分布的不确定性（在测试时，输入存在问题）。

认知不确定性可以通过softmax预测阈值设置或集成方法降低。

我们可以不将OoD不确定性传播到预测中，而是使用一种与任务无关的过滤机制来滤除「有问题的输入」。

密度模型是在测试时过滤输入的一个好选择。但是，需要认识到，密度模型只是真实密度函数的近似，本身也可能易受分布之外的输入的影响。

自我插拔：生成式集成方法能降低似然模型的认知不确定性，所以它们可被用于检测OoD输入。

校准很重要，而且在研究模型中被低估了。

某些算法（分布式强化学习）能将机器学习算法延展成能产出灵活分布的模型，这能比单个风险度量提供更多的信息。