高压连接器电磁屏蔽测试

各位圈内朋友，本期为《高压连接器电磁屏蔽测试》系列文章第三期。 在第一期中我们提到，当频率很高时，屏蔽效率波形出现震荡，如下图所示：

在这一期中，我们将就这一现象进行深入分析，以窥视其中的奥妙。

低频信号的传输                      

我们再次拿出转移阻抗的基本原理图为例：

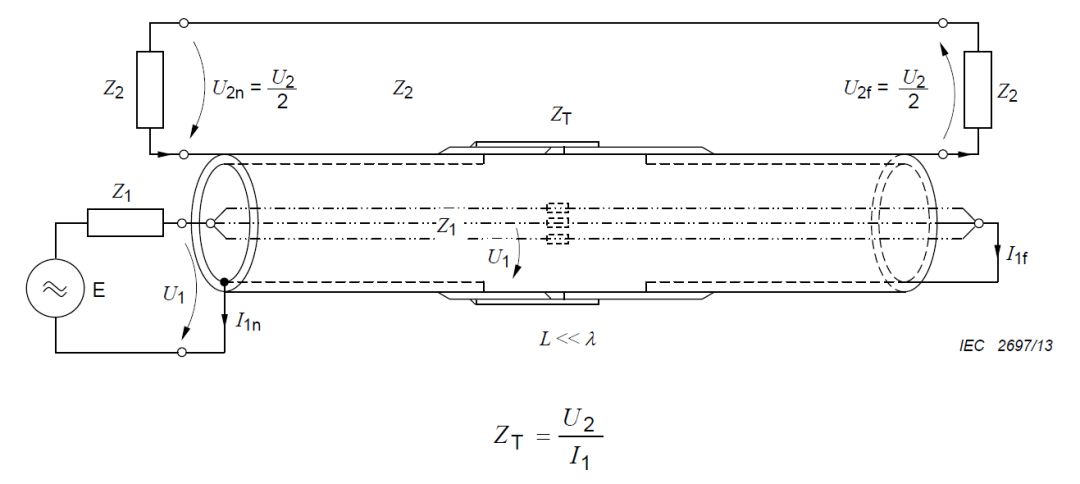
Z1，Z2：分别是内外电路的特征阻抗

U1，U2：分别是内外电路的电压（n:近端，f:远端）

I1：内电路的电流（n:近端，f:远端）

l ：耦合长度

Iλ:真空波长

我们发现，只需要使用加减乘除四则运算，就可以用来分析我们传统的低频电路了，不光简单易懂，而且物理图像也很清晰。

那么高频时会是怎样呢？

高频信号的电路模型：传输线方程      

传输线方程也称电报方程。在沟通大西洋电缆(海底电缆)时，开尔芬首先发现了长线效应：电报信号的反射、传输都与低频有很大的不同。

经过仔细研究，才知道当线长与波长可比拟或超过波长时，我们必须计及其波动性，这时传输线也称长线。

原理图如下所示：

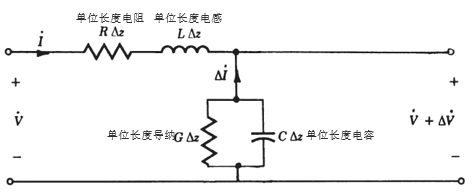
高频情况下，电阻，电感，电容，导纳等参数再也不是集总参数，而必须看作分布参数。

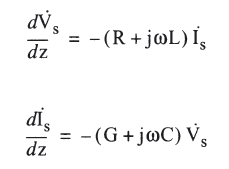
求解上述偏微分方程组，可以得出以下一般解：

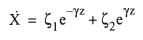
上式中的γ为波传播系数，一般表达式为：

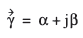
其中α为单位长度的损耗常数，β为单位长度的相位变化量系数

回归到传输线方程，波传播系数如下：

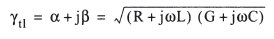
当频率很高时，即电阻分量远小于电感分量，导纳分量远小于电容分量，则波传播系数可以进一步简化为：

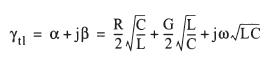
从上式我们已经得出β为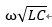，到此，我们确定，高频情况下，电压和电流都因为β而变成了周期波动量。

同轴法测试电路如何重新评估与分析     

三同轴法测试电路，高频信号能量的传播，几乎全部位于导体间的介质中。因为电缆导体为良导体，沿电缆的纵向电场强度分量很小，相对来说，径向电场强度大多了，从而下图圆圈标识的坡印廷矢量，代表了能量的流动。

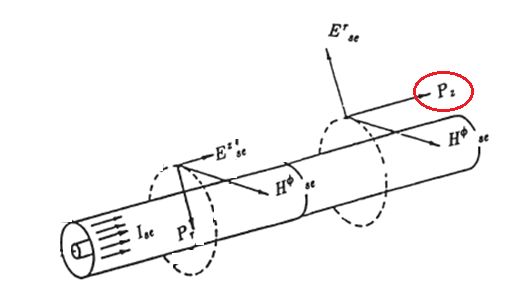
在绝缘介质中，波传播系数为：

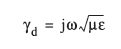
因为信号为高频，整个电缆长度相较于信号波长大很多，所有总的电磁耦合，将通过把所有无穷小长度电缆的耦合作用相加，即求积分。

下图U10为施加干扰电压，U20 为近端被干扰电压，U21 为远端被干扰电压。

积分求解得：

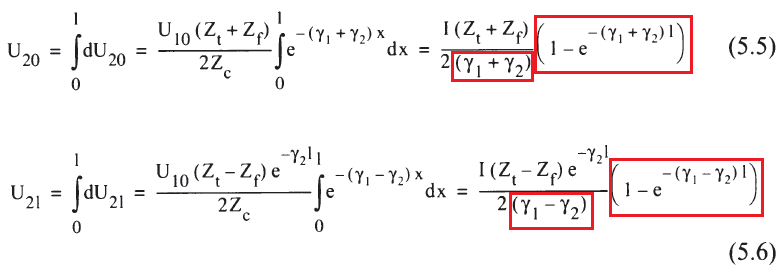
我们研究上式中红框中的公式特性，将其命名为一个如下单独函数：

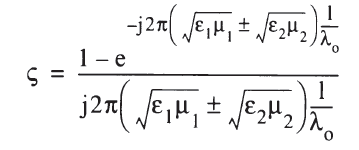
“+”对应着U20，“-”对应着U21。

再进一步简化为：

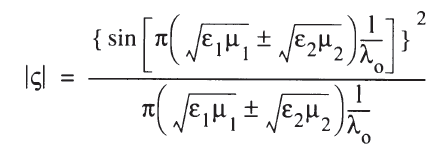
上述方程具有（sinx）^2 / x 的形式，那这个函数的图像如下：

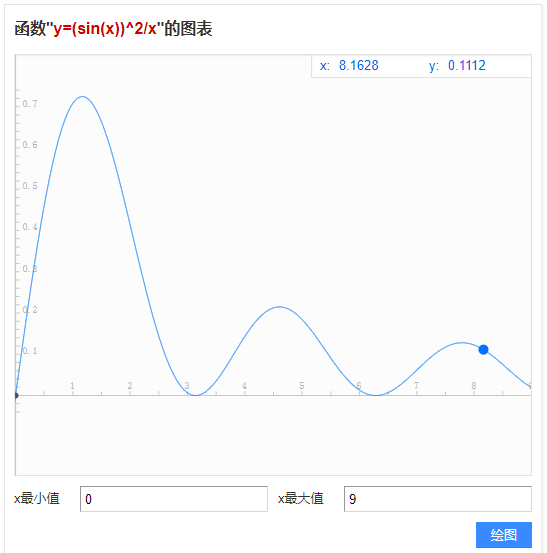
自此，我们最终得到了图形震荡的本质原因。

罗森伯格除了产品，还能为客户提供什么？  

我们的测试团队：

我们的专家：