PCA和KPCA傻傻分不清楚？戳进来教你如何区分

在格物汇之前的文章中，我们讨论了特征抽取的经典算法——主成分分析PCA与线性判别分析LDA的原理与应用场景。PCA是一种无监督的降维方法，寻找的是让数据方差最大的一种映射；LDA是一种有监督的降维方法，寻找的是让数据分类效果最好的一种映射。但是它们仍然有应用的局限性，今天我们就一起来了解下。

PCA的局限性

我们先来回顾一下PCA的降维原理：PCA试图通过旋转找到新的正交基，满足这样的两条性质：

1、最近重构性：样本点到新映射的正交基距离足够接近。

2、最大可分性：样本点在新正交基上方差最大。

最后我们推导得到： 

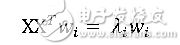
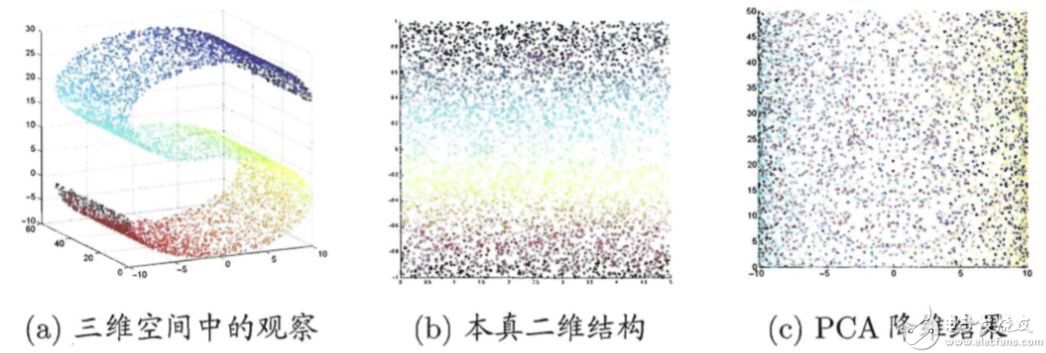
我们只需要对协方差矩阵XX^T 进行特征值分解，得到的特征值和特征向量即是变换矩阵w的解和改主成分所解释的方差量。这样的降维方法是线性的降维方法，即从高维空间到低维空间的函数映射是线性的。然而在不少应用场景中，线性映射可能不能得到想要的结果，例如如下的例子：S型曲线的本真二维结构是其低维空间的原本形状，通过线性降维后得到的结果明显并不是我们所期望的。 

 

核方法

我们介绍SVM的时候所介绍的核方法是一种可以进行升维来生成一些非线性的映射。这个方法我们可以同样使用在PCA降维分析中。

 

假设我们有一个样本集：

x1,x2⋯xn

假设映射函数为，那么映射到高维以后，数据变成：

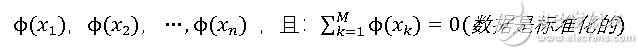
类似于PCA的求解方法， XX^T经过高维映射后得到

，

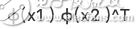故：

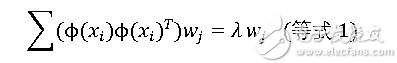
我们把λ 移动到等号左边得到：

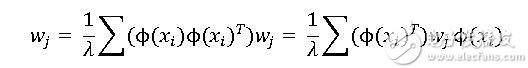
我们令：

做一个简单的替换，得到：

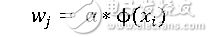
代入等式1，得到：

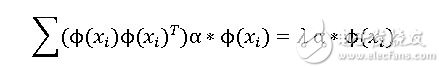
我们在左右两边同时乘上

得到：

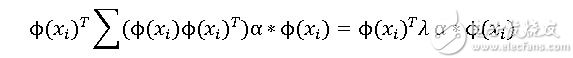
做一下简单的改变：

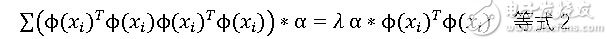
非常幸运的是，我们设计出了

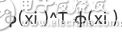
是否还记得我们在SVM的核函数中曾经验证过，在低维空间计算(+1)^2得到的结果与高维空间上计算

的结果相似，只是系数略有不同。因此我们也可以在此应用核方法来计算。我们在此定义核函数矩阵：

代入上面等式2，便可得到：

即

 

很明显，这又回到了特征值分解的问题，取K最大的d个特征值所对应的特征向量即可。

 

小结

我们通过将数据映射到高维以后，巧妙的构建出了

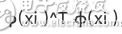
目的是为了通过在低维空间上应用核函数，计算得到跟高维空间上差不多的效果。PCA所做的是对坐标轴线性变换，即变换后的新基还是一条直线。而KPCA对坐标轴做了非线性变换，数据所映射的新基就不再是一条直线了，而是一条曲线或者曲面，如下图所示：

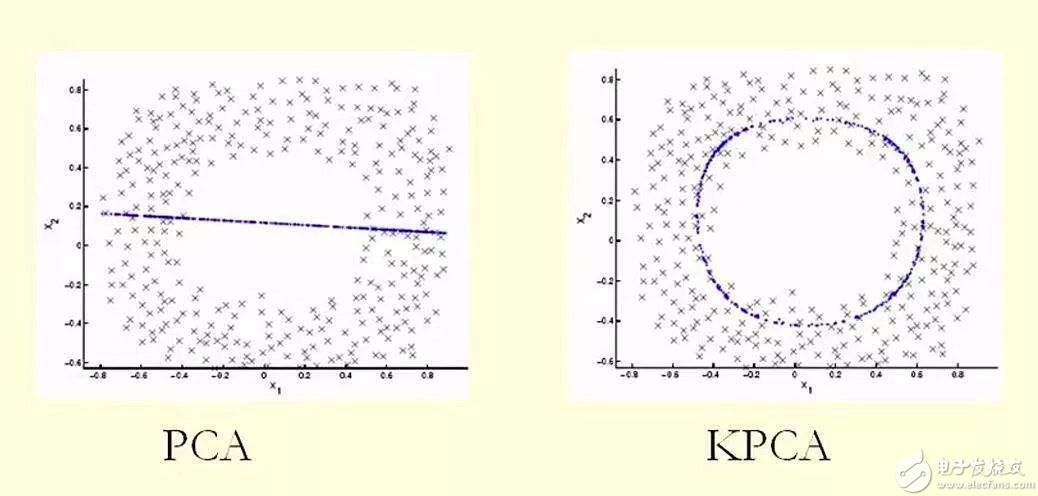
 通过上面这个图，大家应该了解了KPCA和PCA的区别了吧？好了，本期格物汇的内容就到这里，我们下期再见。

 

本文作者：格创东智OT团队（转载请注明作者及来源）