

如何去系统地统计并发现哪些密码是出现频率很高的弱密码呢?
电子说
描述
登入微信需要密码,打开邮箱需要密码,手机支付需要密码⋯,现代人生活离不开密码,但你的密码安全吗?你知道使用你知道使用和很多人一样的密码,不仅仅损害使用者个人的安全性,甚至还会被用于攻击其他用户吗?
即便一般网站会设计规则禁止用户设置诸如 123456 或 qwerty 之类非常容易识别的弱密码,但是对于更“时尚”的弱密码就无能为力了。比如随着《神奇女侠》的热映,流行的密码可能也随之从 superman 变成 wonderwoman。
一群以色列研究人员 ,近日在一场密码学大咖云集的研讨会 RWC 2019 上,提出一种创新方案,使用一种增强了抗干扰能力的多方计算协议,可以在不损害用户密码隐私性的前提下,系统地发现并统计出现的频率很高的弱密码,且统计结果不会被攻击者轻易操纵和篡改。这种方案可用于帮助用户更好地选择自己的密码,降低受到攻击的风险。
如何统计哪些密码最常用?

在这篇论文 How to (not) Share a Password: Privacy preserving protocols for finding heavy hitters with adversarial behavior中,Moni Naor、Benny Pinkas、Eyal Ronen 等人指出,自从1961年麻省理工学院( MIT )在 CTSS 共享操作系统中使用密码以来,现代意义上的密码已经有了半个多世纪的历史。如今随着移动互联网和物联网的蓬勃发展,密码已经渗透到了我们生活中的各个角落。但是很多现实中的例子反复向我们证明:密码并不意味着绝对安全,即使密码是由用户自己选取的。
一方面,密码保证安全的一个前提条件是密码本身必须是随机选取的,即密码含有比较高的信息熵。但是这样的强密码在提供很好的安全性也为记忆带来了很大负担,特别是在现代人需要记住很多个不同账户的密码的情况下。
于是对于那些隔几个月才登录一次的账号,常常会出现登录前必须先重置已经忘记的密码的情况。为了方便起见,很多人实际上会选择比较容易记忆、同时信息熵也较低的密码。
另一方面,由生日或者连续数字/字母构成的弱密码往往非常容易被猜到,并不能起到应有的保护作用。而且流行的弱密码不仅仅损害使用者个人的安全性,甚至还会被用于攻击其他用户。
比如某个网站泄露出明文存储的用户密码以后,黑客就可以选择里面出现频率比较高的密码组成字典,用于攻击其他网站的用户。因为不同网站用户选择密码的分布一般是大致相似的,于是一个网站的用户中流行的密码被另一个网站用户使用的概率也是显著高于随机选取的密码的,黑客便可借此极大地提高攻击的效率。
为了避免弱密码带来的安全性隐患,很多系统会选择禁止使用弱密码,为此需要维护一个常用弱密码的黑名单。这个黑名单包括一些常见的模式和通过以往的密码泄露事件已知的流行密码。
那么问题来了——流行密码往往是随着时代不断变化的,应该如何去系统地统计并发现哪些密码是出现频率很高的弱密码呢?直接统计密码明文显然不是一个好主意,在安全性上有很大的漏洞;即使是统计密码的(未加盐的)哈希值的频率也会带来很多安全上的隐患。Eyal Ronen 所做的报告中就提出了一个解决上述问题的方案。
一位信息泄漏与 The Password Game

要统计常见密码必须满足的第一条要求,就是不要对用户造成伤害,或者尽可能减少对用户的伤害。
从攻击者的角度来看,一个公开的常用密码黑名单,实际上就是一个攻击者梦寐以求的字典,可以用来帮助其猜测用户的密码。此外公开的密码黑名单也可能成为系统被攻击的漏洞。
另一方面,从用户的角度来说,虽然统计用户的密码必然要求记录有关用户密码的信息,但是如果只泄漏密码中的一位的话,其实对于安全性的影响是微乎其微的——因为攻击者只需要多花一点时间就可以猜到这一位信息。
我们可以通过如下猜测密码的博弈游戏来说明:攻击者 A 希望攻击一个设备 D,为此 A 需要选定一个长度为 L 的猜测密码列表,若 D 的密码在列表 L 里,则 A 获得胜利。
在这个博弈中,如果A 在有一位信息泄漏的情况下可以用一个长度为 L 的列表以概率 delta获胜,则另一个攻击者 A’ 只需要选择一个长度为 2L的列表即可在没有泄漏的条件下实现以相同的概率 delta获胜。更进一步,如果使用了具有差分隐私保护的算法,则 A’ 不需将列表长度加倍也可以保持相似的胜率(对于实现了 eps-DP 的差分隐私方案,A’ 使用长度为 L 的列表即可达到不小于 的成功率)。
在计算理论中,寻找常见密码实际上就是解决一个寻找重元素(heavy hitter)的问题,即从一列输入元素中发现出现频率大于一定比例的元素。在这个过程中,我们希望每个用户的密码泄漏的信息不能超过一个比特,以保证用户的隐私性和安全性。另外我们还希望false negative 的概率是可忽略的,即几乎不可能错过任何一个弱密码;对于false positive可以适当放松,但是也希望其概率尽可能小,以减少正常的密码被错误拒绝的概率。

类似的问题之前已经被研究过,不过通常需要一个一定程度上可信的第三方,或者是若干个没有串通的第三方。但是在现实中这些假设都过于理想化了。现实中除了缺乏一个可信的第三方去进行统计以外,还可能出现攻击者试图阻止统计者找到一个弱密码黑名单的情况。为此我们也需要考虑如何避免统计结果被操纵或篡改。
使用传统的多方计算技术可以部分地解决上述问题,即实现对于用户的隐私的保护,但是抵抗恶意干扰的能力比较弱。所以 Eyal Ronen 等人在这个报告里讲到的方案,实际上使用了一种增强了抗干扰能力的两方计算协议。该协议实现的正确性如下:

一个半诚实的方案

这个方案源自于 【BNSTS17】 这篇论文的工作。实现的方式是选择一个输出长度为l 比特的哈希函数,可以把任意长度的密码给映射到长度为 l 的二进制串上,且出现碰撞的概率较低。

然后向每个用户发送一个随机数 r,要求用户返回 r 和 H(password)的内积 v(如下图所示)。收到 v 以后,统计者(服务器)再对所有可能的 x 依次更新 T[x] 的值(T是一个长度为 2^l 的向量)。

通过简单的计算可以验证,如果 x 作为密码的哈希值出现的频率高,则相应的T[x]的值也会很大。因为T[x] 本质上是所有的 x 加上一个随机的噪音。因此只需统计出现频率超过一定阈值的 T[x] 即可得到一个关于常见密码的哈希值的列表。如下图所示。

但是这种方案需要用户一侧比较诚实地配合才行。否则如果用户刻意选择相反的结果,则可以减少相应的密码被统计到的次数,即变相地实现了隐藏一个常见密码的目的。

一个基于平方剩余的方案

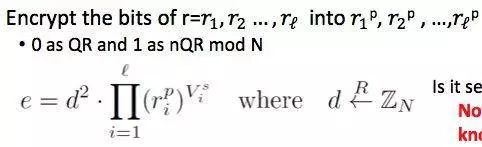
对于两个大素数的乘积 N=pq,很难判断 Jacobi Symbol 为 1 的那些数是否是关于 N 的平方剩余。利用这个性质,我们可以对于每个 v 计算如下的 e,并以此为依据更新 T[v]。 此后的步骤与上一个方案相似。
需要指出的是,上述方案在攻击者知道一个非平方剩余的时候并不安全。但是好在攻击者很难以比随机猜测更好的方法找到一个非平方剩余,且上述方案的安全性可以归约到这个难以找到 nQR 的假设。


作为一个完整的方案,我们还需要用户一方提供一个零知识证明,证明内积运算的结果是正确的。这个零知识证明可以通过 Fiat-Shamir heuristic 改造成非交互式的(参考 Bulletproof,zk-STARK 等)。
关于何时把一个密码识别为“常用密码”的阈值,可以参考下图。

基于平方剩余的方案在实现的性能方面:用户侧的计算需要15秒,且可以在后台运算;服务器侧需要为每个用户花 0.5 秒左右的时间进行验证。
同样的方案还可以用于统计其他场景中的 heavy hitter 问题,例如洋葱网络、设备的 PIN 和 pattern、大规模服务提供商的动态密码分布等。
总结
通过这篇研究可以思考的一个问题是,对于这个统计常用密码的问题,我们是否真的需要(基于计算复杂性的)密码学?
如果用户都是善意的,实际上密码学的构造并不是必须的。但是如果有恶意用户试图操纵统计结果,则不可避免地要用到一些密码学构造。
另外,关于攻击者是否可以利用以哈希值存储的密码黑名单列表,仍是一个有待研究的问题——尽管现在看来这似乎并不可行。
-
关于密码登录系统的问题2013-12-26 2697
-
如何去使用几种公开地国产密码算法呢2021-11-09 2443
-
怎样利用矩阵键盘去制作一种密码锁呢2022-01-20 1252
-
基于FPGA的密码传输系统设计2010-08-09 534
-
如何在忘记密码时怎么登录Windows XP系统2009-02-12 5103
-
电脑各类密码的清除2010-01-14 899
-
密码技术,密码技术原理是什么?2010-03-20 1435
-
若忘记了Linux系统的root密码,该怎么办?2018-10-15 13213
-
密码会在安防系统中消失吗?2019-09-26 2487
-
弱密码是什么?有什么用?应用在哪?2020-12-28 10199
-
不知道嵌入式Linux系统下的root密码,修改新密码并进入系统2021-11-01 2554
-
为了帮助企业消灭“弱密码”,芯盾时代搞了点黑科技2023-10-25 880
-
oracle操作系统用户不改密码的理由2023-12-06 1064
-
Linux系统设置用户密码规则(复杂密码策略)方法2024-12-07 2225
-
NAS重置密码攻略来袭,让你告别‘密码焦虑’!2024-12-11 2056
全部0条评论

快来发表一下你的评论吧 !

