

如何使用CRC算法检查数据传输的正确性
电子说
描述
还有半个多月就要过年了,工作之后时间过得真是飞快啊,才刚刚熟悉在各种文件上签2018的日期,现在竟然又变成2019了。最郁闷的是又老了一岁,找谁说理去
大家都知道芯片有输入输出,根据不同的传输协议,输入输出的数据有可能是一串长长的数据,几十个或者几百个byte甚至更多。在数据传输过程中,由于某些意外的原因导致某些bit出现错误(0变为1,或者1变为0),从而接受方接收到错误的数据。
为尽量提高接受方收到数据的正确率,在接收方接收数据后需要对数据进行校验,当且仅当校验的结果为正确时接收方才真正收下数据。循环冗余校验(Cyclic Redundancy Check, CRC)算法通常用于数字传输系统或者存储器中,用来检测意外事件对原数据的影响,判断接受到的数据是否正确。
下面是IC君文武双全的朋友文武写的CRC文章,IC君稍微做了优化排版和少量的编辑工作提升大家的阅读体验。
1
前言:
因为CRC循环冗余校验码的算法和硬件电路结构比较简单,所以CRC是一种在工程中常用的数据校验方法。尽管CRC简单,但在工程应用中还是有些问题会对工程师产生困惑。这篇文章将从以下三个方面介绍以下CRC,希望对大家有所帮助。
CRC 的数学原理;
CRC的通项公式,怎样选取一个适合的通项公式;
CRC 硬件电路实现,串行电路到并行电路的实现。
2
CRC的数学原理:
在讲CRC的数学原理之前,首先看一下下面的图。图1是A要给B发送1bit的信息0或者1。假设A发

图1
送一个0给B,系统正常的情况下B会接受到一个0。但是如果有个干扰(比如信号线的串扰)在A和B相连的传输线上,那么B就有可能接受到一个1,传输数据发生错误。
为了改进这个传输过程,A和B约定(图2)。

图2
如果A要发送一个0给B,A就在一段时间连续发送两个0(2’b00’)给B;
如果A要发送一个1信息给B,那么A就在一段时间连续发送两个1(2’b11’)给B。
如果B接受了一个2’b01或者2’b10,B就知道他们之间有干扰;
要是B接受到了一个2’b00,B就会认为A发送的信息是个0;
那么A有没有可能发的信息是2个1?这也是有可能的,不过2’b00变成2’b11比1’b0变成1’b1的概率要低的多。
如果A和B约定以图3的方式进行传输,假设A要发送一个0给B,那么A就在一段时间连续发送3个0(3’b000)给B;如果A要发送一个1信息给B,那么A就在一段时间连续发送三个1(3’b111’)给B;
如果B接受到的值为3’b001、3’b010或者3’b100,B就知道他们之间有干扰,

图3
并且B会自我判断A给自己发送的信息是0不是1。这种判断是合理的,因为误判的概率很低。
图1,图2,图3可以概括成图4。

图4 箭头上的数字是海明距(HD)
海明距离HD的定义
两个码字的对应比特值不同(异或)的总数目称为这两个码字的海明距离。一个有效编码集中,任意两个码字的海明距离的最小值称为该编码集的海明距离。
图4的第一种情况就是没有编码,0和1的码距(HD海明距)是1;
第二种情况其实就是奇偶校验,码距是2,可以检测1个错误;
第三种情况就是纠错码了,海明距是3,如果出现了1个错误是可以自己纠错的,出现小于3个错误可以检测。
第三种情况的有效码字000,其中0是信息位,00是校验位,2位的校验码来确定一位数据位,看上去有点太浪费了。
一种编码的校验和纠错能力取决于它的海明距离。为检测出d比特错,需要使用码距d+1的编码;因为d个单比特错决不可能将一个有效的码字转变成另一个有效的码字。当接收方看到无效的码字,它就能明白发生传输错误。
同样,为了纠正d比特错,必须使用码距为2d+1的编码,这是因为有效码字的距离远到即使发生d个变化,这个发生了变化的码字仍然比其它码字都接近原始码字。
通过上面的例子大家理解了码字(CODEWORD),信息位(DATA),校验位(CHECK SUM),海明距(HD)等概念。
下面看一看图5的CRC计算过程

图5(来自wikipedia)
CRC在数学上就是除余运算,除数是个通项公式(固定数),
例如G(X)=X3+X+1 (1011),
被除数11010011101100,除数1011
DATA=11010011101100,
最终得到的余数 CHECK SUM=100,
所以需要传输的CODEWORD=11010011101100100。
用上面CRC算法作为A和B的通信协议,传输数据只添加了3bit的checksum,编码效率比图2、图3提高不少。但是编码和解码算法会变复杂,所以有得必有失吧。
具体传输过程如下:
A发送DATA=11010011101100给B,
发送之前先编码
假设初始CODEWORD=11010011101100000
对G(X)=X3+X+1 (1011)除余数,
最后用初始DATA加上CHECK SUM=100得到最终发送:
CODEWORD=11010011101100100。
在B接受到CODEWORD 通过解码来检查A的发送有没有错。
解码的过程:
用CODEWORD=11010011101100100对G(X)=X3+X+1 (1011)除余数,如果余数等于0即CHECK SUM=000,就认为B接受到的数据就没有问题。

图6
余数等于0,就一定没有出错吗?当然不是,只能说出错的概率很低。这个可靠性跟CRC的G(X)通项公式和信息位的长度相关;
怎样选取一个适合的CRC通项公式呢?
CRC通项公式(生成多项式)很容易找到,网上随便一搜就会有很多。

图7(来自wikipedia)
生成多项式有很多表示方法,CRC3多项式表示法G(X)=X3+X+1;数字表示法0x3、0x6、0x5等。数字表示法简洁,在用软件语言实现CRC算法时常用。
提醒一下:当看到代码poly=0x03,很难知道多项式是什么?因为数字表示法没有统一的定义,容易产生歧义。建议写数字表示的时候附上多项式,这样不会产生误会;程序变量poly=0x03,最好后面是注释G(X)=X3+X+1。
下面总结一下数字表示法图8,CRC的最高位和最低位系数都有。这些表示法无非就是顺序排列丢掉高位或者低位;或者逆序排列丢掉高位或者低位。

图8
数字表示法这样定义是为了遵循CRC的研究者的习惯。
CRC多项式的检错能力其实有很多研究成果,这里以koopman phail举例,因为可以在作者的个人主页上找到一些算好的数据。作者还是美国著名的卡内基梅隆大学的Associate Porofesor。
在讲他的成果之前,先还是给出一下一些概念。用图6的CRC3的多项式 G(X)=X3+X+1编码:
DATA=11010011101100,
CHECK SUM=100,
CODEWORD=11010011101100100。CRC3就3个校验位最多也就8个状态,要编码的DATA=11010011101100有14位,总共就有2^14种可能的接受DATA,这么多的DATA肯定有很多校验位是相同的。
校验位CHECK SUM=100的DATA变成相同校验位但是数据不同的DATA1,在接受端是没有办法知道出错了的。所以koopman phail就把“几乎所有的多项式”做了统计,这些多项式随信息位DATA的长度的变化对应CRC多项式的海明距HD的关系。
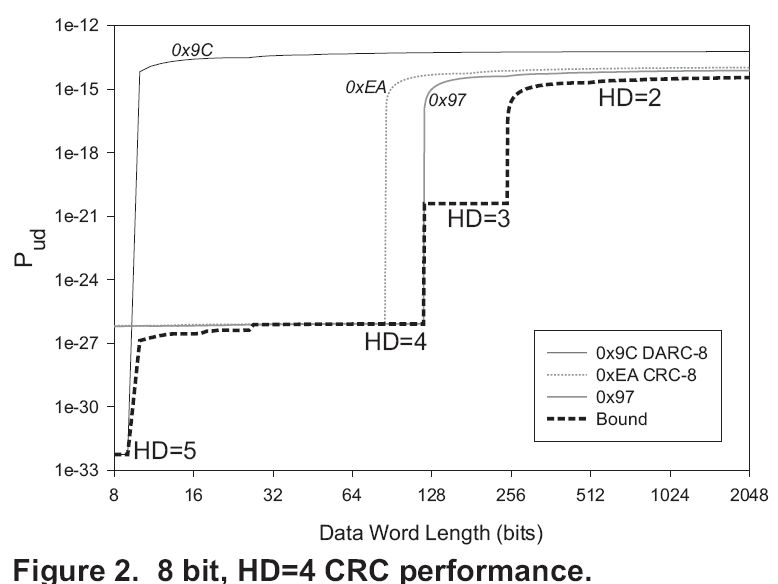
图9就是论文中的一张图,虚线表示所有CRC8多项式的海明距的边界,横坐标表示的信息数据的长度;纵坐标表示误码率,误码率越小越好。
如果信息位是8bit以下,0x9C是比较好的多项式;
如果信息位是16bit到64bit之间, 0xEA和0x97都是比较好的多项式。
其实普通人也可以统计出来的,只要每个长度的DATA都穷举所有的码字空间再把它们的海明距找到就行。但是计算过程的运算量还是很大的,作为工程师去查koopman phail给的表就好了。如果你还是不够用,可以去koopman phail的主页上去找。
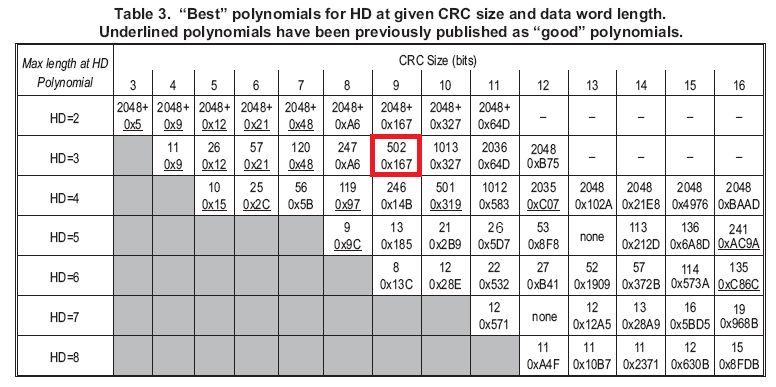
图10
现在根据图10的表格来选个好的多项式,假设CRC需要检测2(HD=3)错误,你的信息位DATA的长度是256bit那就选0x167多项式。
-
基于Verilog语言实现CRC校验2025-03-24 2267
-
虹科技术|保障数据传输稳定性:BabyLIN产品的CRC算法实现2024-01-02 1213
-
瑞萨RA MCU中CRC模块的使用方法2023-12-07 3346
-
单片机中几种常见的校验算法介绍2023-06-05 2719
-
如何正确实现EndDevice和Coordinator之间的数据传输?2023-03-24 777
-
CRC是什么意思2021-08-11 1481
-
USB数据传输中CRC校验码的并行算法实现2021-03-28 1128
-
关于MSP430微处理器的光无线数据传输系统2018-04-25 1088
-
crc校验错误_crc校验错误怎么解决2017-12-05 49502
-
crc校验方法及示例2017-12-04 16467
-
如何为STM32编程节省代码空间?在IAR中配置CRC参数有窍门2017-09-06 14952
-
数据传输速率是什么意思2010-03-18 5178
-
Modem数据传输标准2009-12-28 1284
-
数据传输2006-03-25 875
全部0条评论

快来发表一下你的评论吧 !

