边界元法的功能、案例与相关的后处理技巧

COMSOL Multiphysics® 软件“声学模块”中的基于边界元方法（boundary element method，简称 BEM）建模物理场接口可以和基于有限元方法（finite element method，简称 FEM）的接口无缝耦合，从而对声-结构相互作用等问题进行建模。本文介绍了边界元法的功能、案例与相关的后处理技巧。

基于边界元方法进行声学建模优势

“声学模块”的压力声学，边界元 接口提供了 BEM 功能。该接口适用于求解每个域内的材料属性均为恒定值的二维和三维声学问题。通过采用复值材料属性，用户可以在流体模型中引入损耗。此外，边界元接口还可以进行散射场仿真，也就是说它能够处理散射问题（见下图）。借助新的边界元法，用户能够求解以前不支持的问题类型，下文将进行详述。

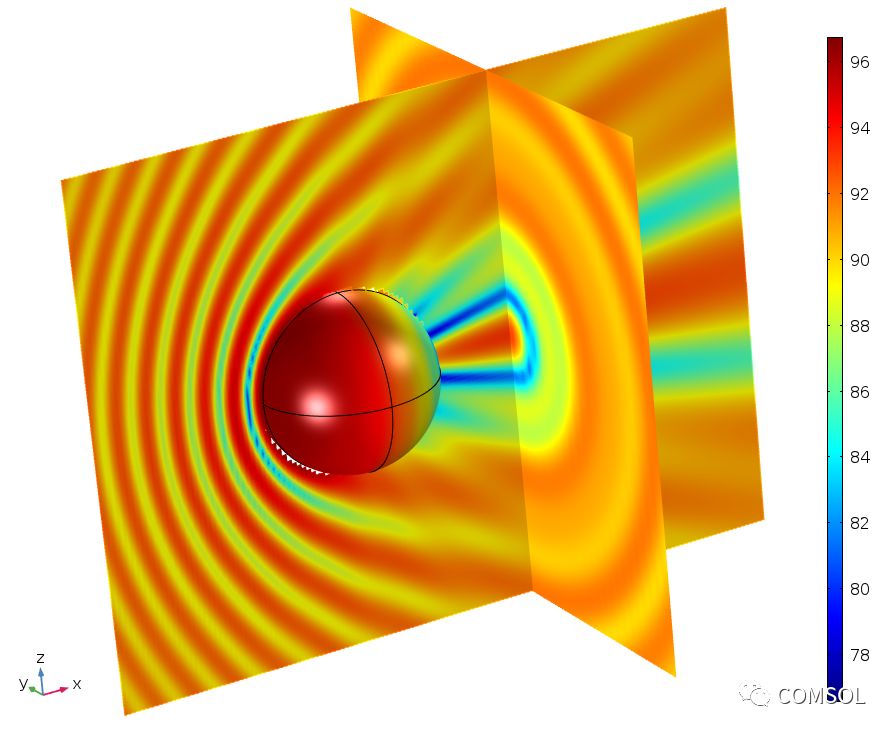
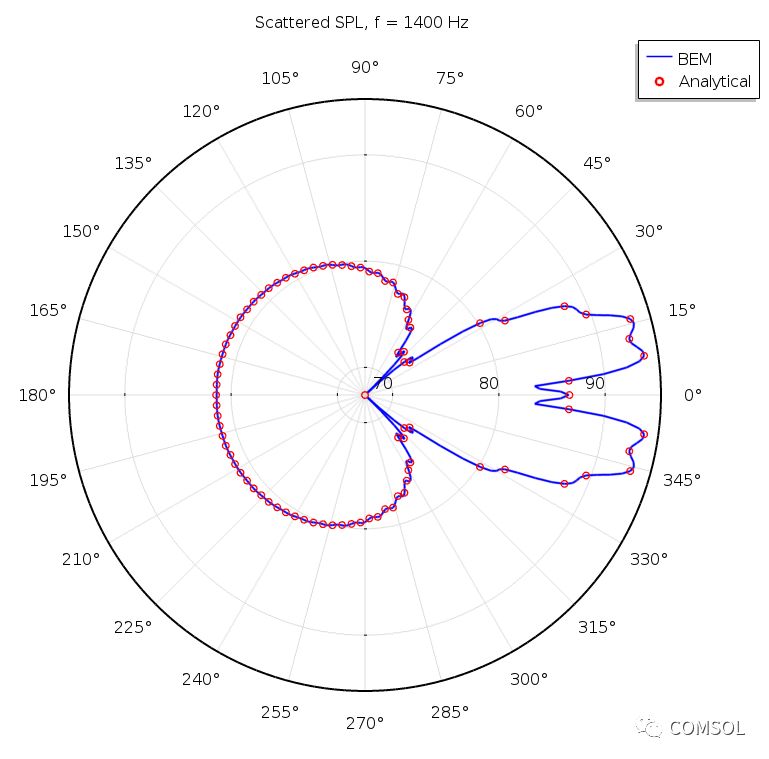
球形散射体的经典 BEM 基准模型，图片比较了模型结果与解析解。上图显示 500 Hz 频率下两个截面的声压级，下方的对比图显示了 1400 Hz 频率下的散射场。图片来自球形散射体：BEM 基准教学模型。

将基于 BEM 和 FEM 的接口相互耦合是软件的一项重要功能。例如，利用声-结构边界 多物理场耦合将声学 BEM 接口与基于 FEM 的振动结构相互耦合；通过声学 BEM-FEM 边界 多物理场耦合使 BEM 和 FEM 声学域相结合。

出色的灵活性使得用户可将 BEM 和 FEM 应用到最合适的场景中，而且与 COMSOL Multiphysics 的所有其他物理场耦合一样，所有操作均在一个用户界面中完成。举例来说，FEM 可以添加更通用的材料属性，因此适合模拟振动结构的内部域，比如封闭的空气域；外部域则使用 BEM，因为它更适合对大型域和无限域建模。下图中的扬声器模型采用了两种方法。

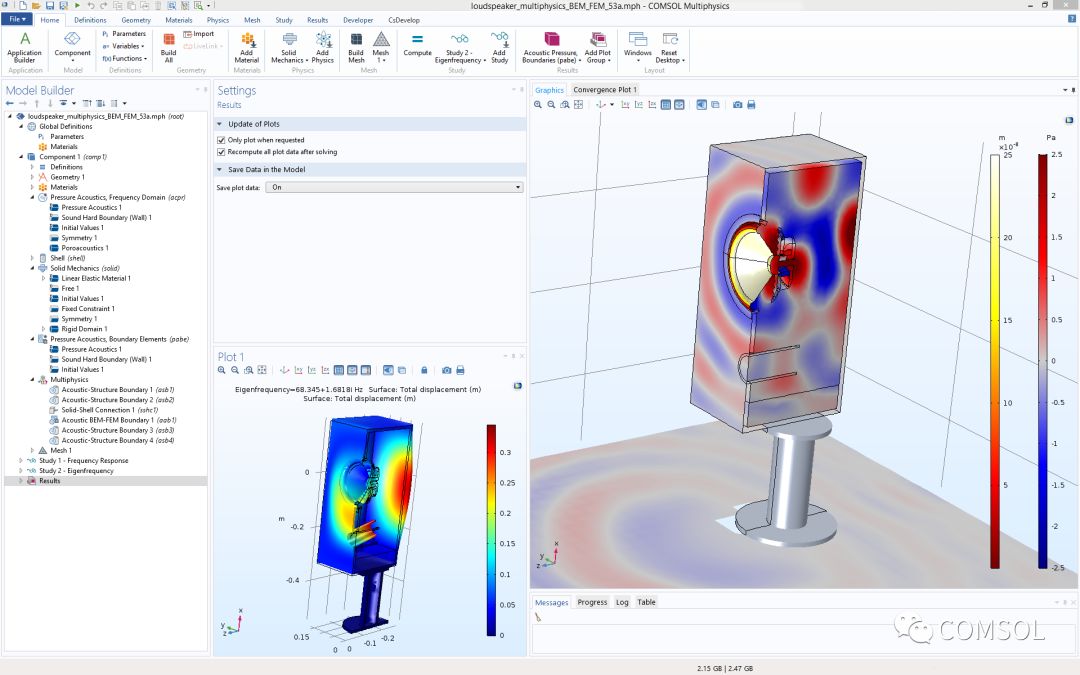
扬声器多物理场模型的 COMSOL Multiphysics 用户界面，模型包含 BEM 和 FEM 声学以及 固体力学和 壳接口。物理场被耦合到内置的多物理场耦合中。图片来自振动声学扬声器仿真：基于混合 BEM-FEM 法的多物理场教学模型。

利用边界元法，我们只需对邻近建模域的表面划分网格。这意味着不需要对大型体积进行网格划分（有限元法则不然），因此基于 BEM 的接口尤其适用于涉及辐射和散射，且拥有详细 CAD 几何的模型。该接口还提供了内置条件，供用户设置无限硬声场边界（壁）或无限软声场边界。这些边界条件对建模十分有利，例如在水下声学问题中，无限软声场边界可用于模拟海洋表面。

对于包含大型流体域的问题，基于 BEM 的接口通常更具优势，若使用 FEM，就必须创建对大型体积进行网格划分，而较大的三维网格会导致内存溢出。针对类似情况，边界元法甚至能够拓宽 COMSOL Multiphysics 可处理的问题类型。这些问题的一些相关示例包括：

无限壁或无限软声场边界与辐射对象相距很远（就波长而言）的模型

散射对象和辐射对象相距很远且发生相互作用的模型

复杂非紧凑几何的辐射问题，对此类问题使用 FEM 时，很难施加合适的辐射条件或完美匹配层（perfectly matched layer，简称 PML）

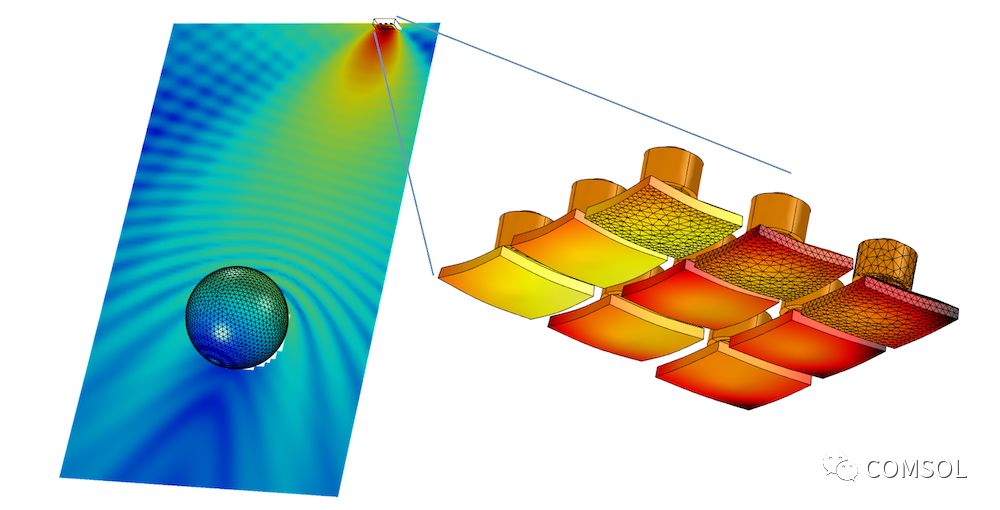
与散射对象相距很远的换能器阵列的示例图。由于内存需求很大，这种问题很难或者不可能单纯利用有限元法来求解。边界元法适用于求解此类模型（将球体移动到远处不会增加计算量）。图片来自声纳系统的蘑菇形换能器阵列教学模型。

针对相同数量的自由度（degrees of freedom，简称 DOF），边界元法对计算能力的要求比有限元法更高，但另一方面，要获得相同的精度，边界元法要求的自由度一般比有限元法少得多。BEM 可生成完全填充且密集的系统矩阵，因此它需要使用与 FEM 不同的专用数值方法。在求解小型和中型声学模型时，基于 FEM 的接口——例如压力声学，频域 接口——的速度通常比 BEM 更快。

根据“声学模块”的用户指南，压力声学，边界元 接口的边界元法是基于一种利用 Costabel 对称耦合的直接方法。为了对所得的线性系统进行求解，我们利用了自适应交叉近似（ACA）快速求和算法。该方法使用了部分装配矩阵，该处矩阵与向量相乘的效果得以计算。缺省迭代求解器为 GMRES。内置的多物理场耦合降低了无缝创建混合 FEM 和 BEM 物理场问题的难度。在求解耦合模型时，对 BEM 问题采用默认的 ACA 混合算法，对 FEM 使用合适的预条件器（直接或多重网格）。

两全其美的方法：混合 FEM-BEM 法

如上文所述，压力声学，边界元 接口可与基于有限元的接口中无缝耦合，比如压力声学，频域 接口和固体力学 接口。借助耦合，创建混合 FEM-BEM 模型变得很轻松，而且模型能够在最需要和最合适的地方充分利用方程各自的优势。

BEM 不等于替代声场中的有限元，而应该看作一种补充。按照经验，由于基于 FEM 的模型在求解时需要非常细化的网格，所以大型流体域应该选择 BEM，或者将基于 BEM 与 FEM 的物理场耦合到一起。下面是一些应用和示例：

模拟具有复杂几何的换能器和辐射问题

利用 FEM 模拟（压电式或电磁式）换能器，与此同时利用 BEM 模拟外声场

耦合内部和外部问题

对狭窄区域和共振体使用 FEM，对辐射区域使用 BEM

请牢记：声学 BEM-FEM边界 多物理场耦合可以帮助用户轻松耦合基于 BEM 和 FEM 的声学模型

对于内存足够的较小模型，有限元法通常更快。利用辐射条件或 PML的传统方法适合模拟开放的辐射域。

压力声学，边界元 接口可用于替代基于 FEM 的辐射条件/PML 以及远场计算特征。参见下图中的模型示例。

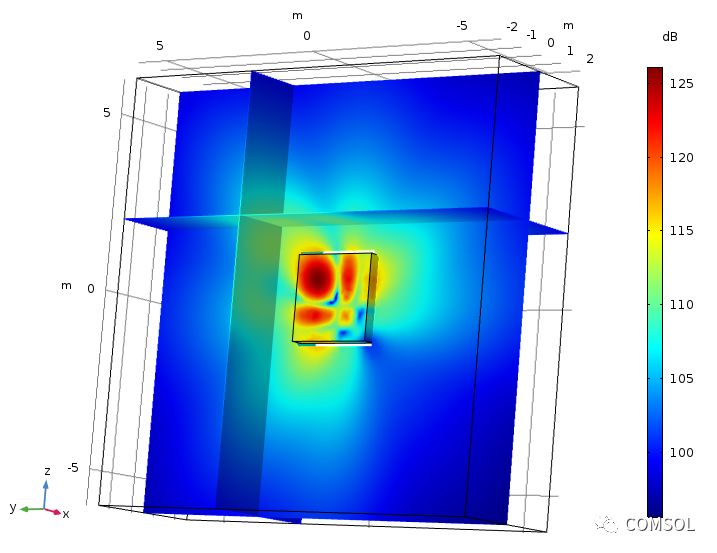
在贝塞尔面板教学模型中，压力声学，边界元口被用来模拟开放空间。边界元接口可以有效地替代原本需要的辐射条件（或 PML）和远场计算特征。图片展示了 FEM 域（多个点源位于该域内）内的表面声压级，以及外部 BEM 域在特定范围内的三个截面的声压级。

BEM 模型的后处理

当使用 BEM 接口求解问题时，所得的解由边界上的因变量——相当于未知场变量——组成，其中包括压力 p 及其法向导数；也就是法向通量变量  pabe.pbam1.bemflux。域内的解是以计算积分内核为基础的，这是 BEM 的核心。

边界上定义了专用的边界变量。该变量在外部和内部边界上拥有不同定义；在外部边界上，它等于因变量。在内部边界上，则被定义为向上和向下压力相关变量（pabe.p_up 和  pabe.p_down），因为此处压力是不连续的；比如内部硬声场壁 边界。此外，所有边界上都有预定义后处理变量，必要时，这些变量能够将边界变量与基于内核计算的变量的属性组合在一起。

如下图所示，我们可以在绘图的替换表达式 列表中找到上述变量以及所有其他后处理变量。

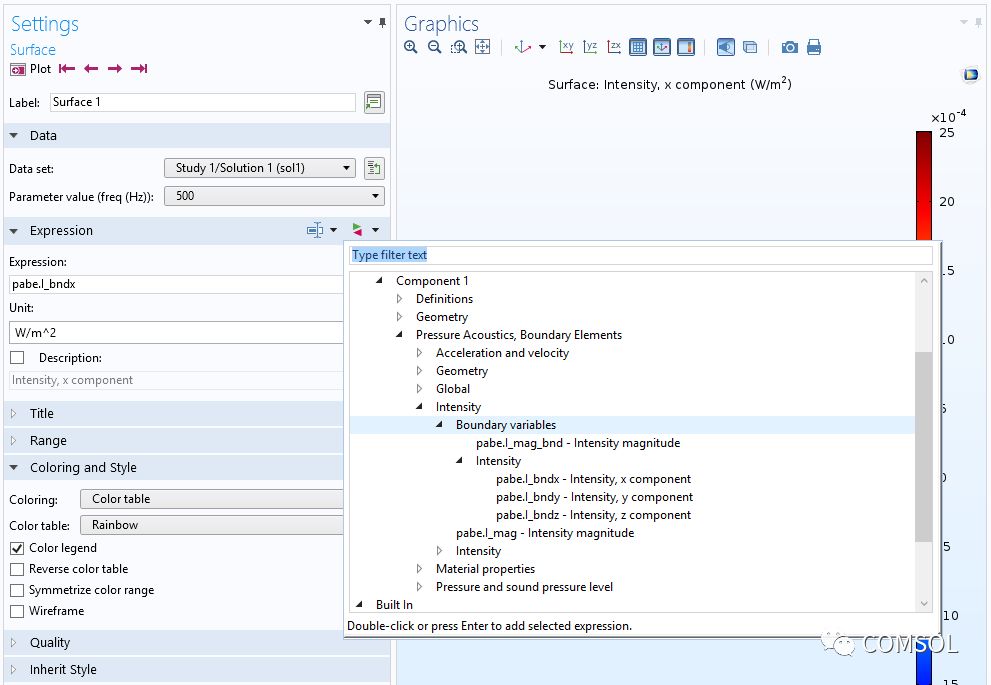
用户界面截图显示了一部分预定义后处理变量的列表。

在域内对 BEM 解进行后处理时，必须使用上文提到的 BEM 积分内核计算来重构压力场。为了使 BEM 解更易于可视化，我们可以在栅格上自动执行内核计算，从而生成专用的数据集。下面几段讨论了可用于绘制声学结果的数据集。

三维栅格 和二维栅格 数据集专门求解没有网格的域。这些数据集在待求解的区域建立了由点组成的规则栅格。栅格的尺寸和边界以及解析度（栅格间距）均可修改。对波动问题进行可视化时，充足的空间解析度非常重要。然而，解析度不应过大，否则会增加渲染时间。

栅格数据集还有其他用途，例如用作切面图或表面图的输入数据集。在求解 BEM 模型时，系统会自动生成栅格数据集和多切面图，并将其应用到默认的绘图中。栅格数据集还能用作截面、截线或者截点的输入。

只要勾选仅计算全局定义的表达式 选项，就可以直接利用参数化曲线和表面计算 BEM 的解。

BEM 变量被用作输入时，我们可以直接使用专门的声学绘图。相关示例包括用于绘制空间响应的远场 图（不一定是远场，实际上可以是任何距离）以及方向性 图。举例来说，声压级变量 pabe.Lp 可以用作表达式。

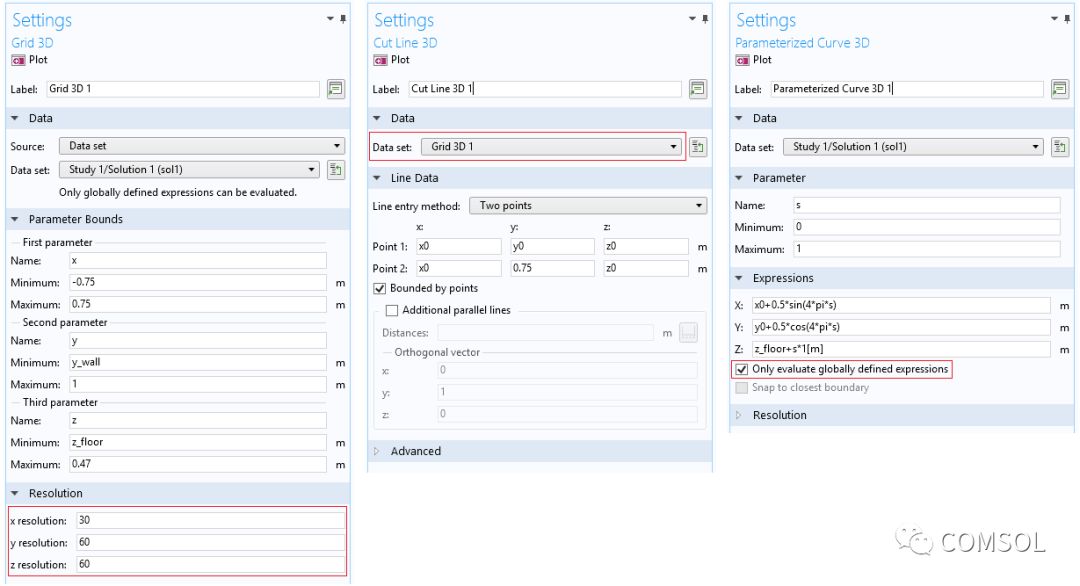
用户界面截图显示了上文提及的一些不同的数据集。重要设置已突出显示。

上方截图摘自扬声器辐射：BEM 声学教学模型。该模型求解辐射问题，并且创建了多数常见绘图和结果可视化效果。

下图显示了利用扬声器表面的栅格绘制在三个切面上的声压级。为了表现后处理与可视化工具的通用性，图片还沿着使用参数化曲线 三维数据集创建的参数化螺旋曲线绘制了声压级结果。

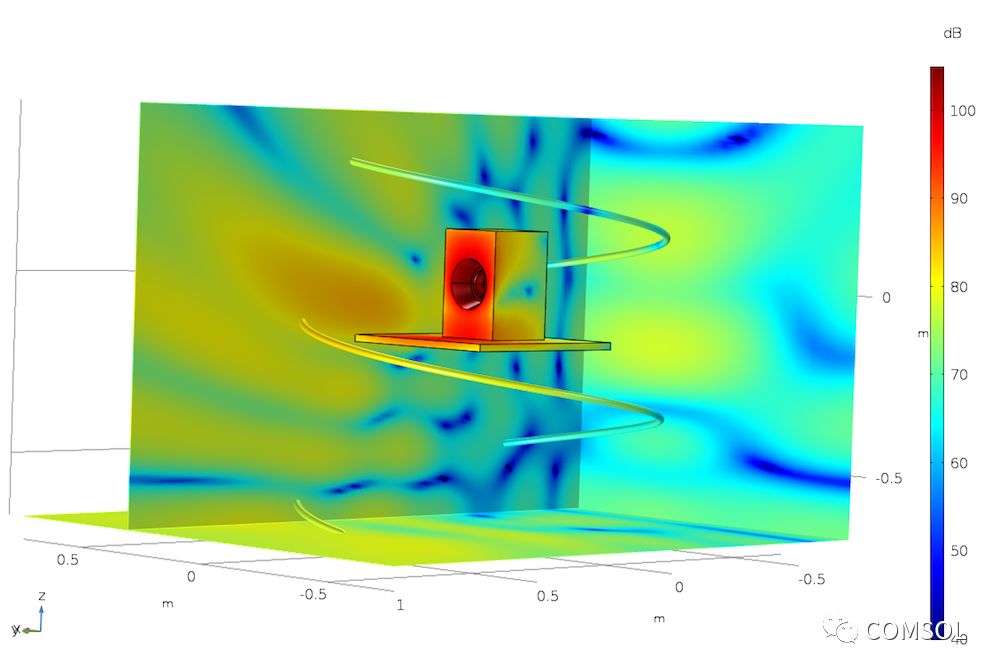
“扬声器辐射：BEM 声学”教学模型以多种方式显示声压级结果。

使用边界元法的两种特殊情况

接下来，我们将讨论使用边界元法时两种需要特别考虑的情况。

第 1 种情况：半空间辐射问题

很多声学应用都涉及了一种情况：换能器位于一个无限挡板内，并朝向半空间辐射。大多数情况下，此类装置不能使用 BEM，至少在包含无限挡板的情况下绝对不行。非无限挡板可以使用内部硬声场壁 等边界条件来创建。

我们通常习惯使用无限硬声场边界 特征。该边界条件不能用于像扬声器驱动器立着的挡板那样“中间有一个洞”的边界。因为 BEM 方程基于全空间格林函数，所以无限对称平面或无限壁条件意味着平面或壁必须无限延伸，而且不能有开口。基本上，如果边界在物理场接口中拥有对应的选择，且选择处于活动状态，那么这些边界必须位于无限边界条件的同一侧或者位于无限边界条件上。否则将产生非物理结果。

针对如何设置无限挡板，我的一般建议是将基于 FEM 的物理场接口同远场计算特征及 PML 或辐射条件结合使用。扬声器驱动器的集总模型就是一个例子。这种设置通常快得多！

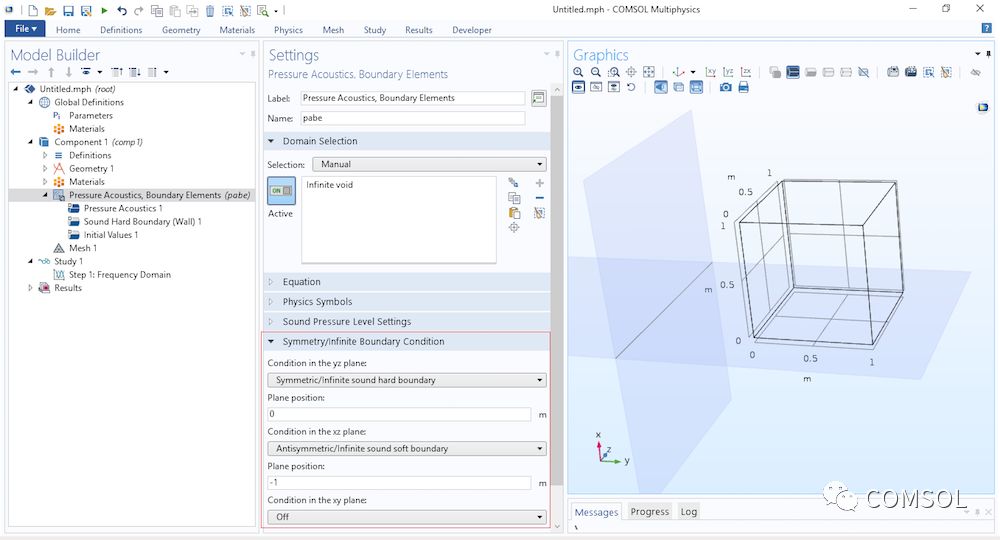
压力声学，边界元接口的用户界面。物理场顶层设置了无限边界条件（突出显示）。选定任意条件后，生成的平面将显示在“图形窗口”中。

第 2 种情况：内边值问题

内边值问题——特别是没有或产生很少损耗的锐共振问题——很难使用 BEM进行求解。问题的原因不在于方法本身，而是因为使用了迭代求解器来高效求解底层矩阵系统。基于 FEM 的模型使用迭代求解器时也会出现相同的问题。

在靠近锐共振的地方，任何细微的变化都会导致压力变化，但是我们很难捕捉这种变化来确保收敛。如果可能的话，遇到这些情况时，建议结合使用 FEM 和直接求解器，或者添加真实的带损耗的边界条件，例如阻抗条件。

关于 BEM 的结语

在 COMSOL Multiphysics 软件环境中，BEM 是对 FEM 的实用补充。众多从事声学建模的工程师都期望着增加这项功能。我们希望你会喜欢“声学模块”的这项新增功能。

下一步操作

点击下方按钮，探索附加的“声学模块”产品提供的专业声学建模功能还可以实现哪些应用。

亲自动手操作：下载本文中的教学模型。访问“案例下载”页面，登录 COMSOL Access 账号后即可下载 MPH 文件。

球形散射体：BEM 基准

声呐系统的蘑菇形换能器阵列

振动声学扬声器仿真：基于混合 BEM-FEM 法的多物理场

贝塞尔面板

扬声器辐射：BEM 声学教程