详解机器学习算法流形学习

在格物汇之前的文章中，我们系统性的介绍了特征抽取的经典算法——主成分分析PCA与线性判别分析LDA的原理、应用场景，以及这两种算法的局限性和改进方法。今天的格物汇要给大家介绍一种新的机器学习算法——流形学习。

流形学习

流形学习是一类借鉴了拓扑流形概念的降维方法，与核PCA的目的一样，它想要在低维空间中尽量保持在高维空间中的结构。一个形象的流形降维过程如下图，我们有一块卷起来的布，我们希望将其展开到一个二维平面，我们希望展开后的布能够在局部保持布结构的特征，其实也就是将其展开的过程，就像两个人将其拉开一样。

流形学习方法有很多种，但是他们具有一些共同的特征：首先构造流形上样本点的局部邻域结构，然后用这些局部邻域结构来将样本点全局的映射到一个低维空间。它们之间的不同之处主要是在于构造的局部邻域结构不同，以及利用这些局部邻域结构来构造全局的低维嵌入方法的不同。下面我们简要介绍两种最常见的流形学习方法：Isomap和LLE。

Isomap

高维数据结构可能太过于抽象，很难去理解。我们先来看一个具体的实例：在上一篇文章中，我们所看到的三维空间上的数据是呈现”S”型，假设我们想寻找图中两点的测地距离（延曲面距离），就不能用这两点坐标所计算的欧式距离，如下图（a）黑色线所示，因为黑色线所构成的路径延曲面不可达。而应该使用其沿着“S”形曲面所生成的距离，想象一下一只蚂蚁在数据曲面上爬行，它不能脱离曲面行走，行走的路径如下图（a）红色线所示。下图（b）则显示的是两条线本真二维结构上所显示的路径，很明显红色的线更加真实的反映了两个数据点在三维数据上的距离。

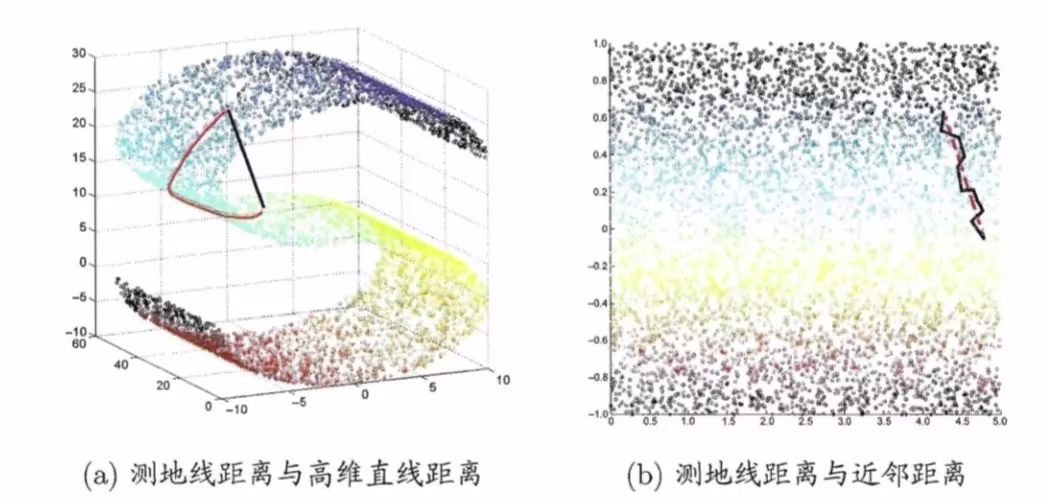
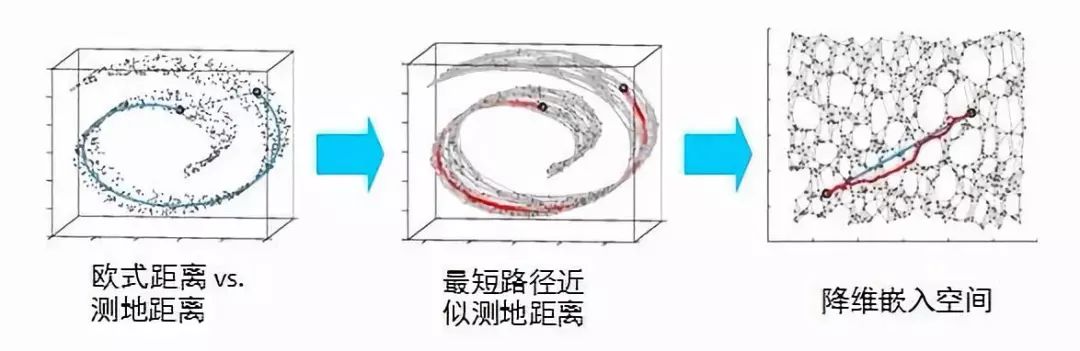
上述这种寻找数据曲面测算距离的方法称为Isomap（等度量映射），它是流形学习中的一种方法。它是如何实现的呢？它假设数据点与K个最近邻的点可以构成一个子集，这个子集可以用普通的欧式距离来衡量，而这个子集中的点又与其他子集中的点相连，这样两个目标点的距离就可以分解成若干子集的欧式距离叠加来近似得到，最后这些相连的点可以降维到低维空间中展现出来。

局部线性嵌入（LLE）

流形学习另外一个典型案例是局部线性嵌入（LLE）。Isomap假设近邻的测地距离可以用欧式距离来表示。而LLE则假设在近邻内可以用线性加权互相表达。比如对于任意一个样本x0，我们都可以用他附近的几个点x1 x2 x3 x4的线性组合表示出来，即

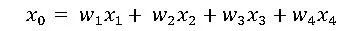
经过LLE降维投影后，原来的点x0 x1 x2 x3 x4，投影变成了

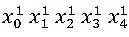
LLE降维的想法是，降维后尽量去保留高维时的线性组合关系：

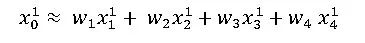
如何求解呢？我们需要先求出线性组合的权重w，对于样本x0我们需要找到其最近的k个其他样本点，假设为x1 x2 x3 x4，我们根据线性表示误差最小来求出w：

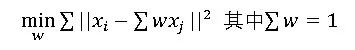
根据上式确定出线性组合的w以后，我们还需要让其在低维空间也能尽可能满足线性组合的表达关系式，也就是说对于x0 x1 x2 x3 x4……的低维投影点z0 z1 z2 z3 z4……满足：

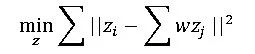
两个优化目标函数类型很像，但需要明确的是第一个目标函数优化的是权重w，而第二个目标函数优化的是降维后的坐标z。经过优化即可得出样本集在低维空间上的投影坐标。

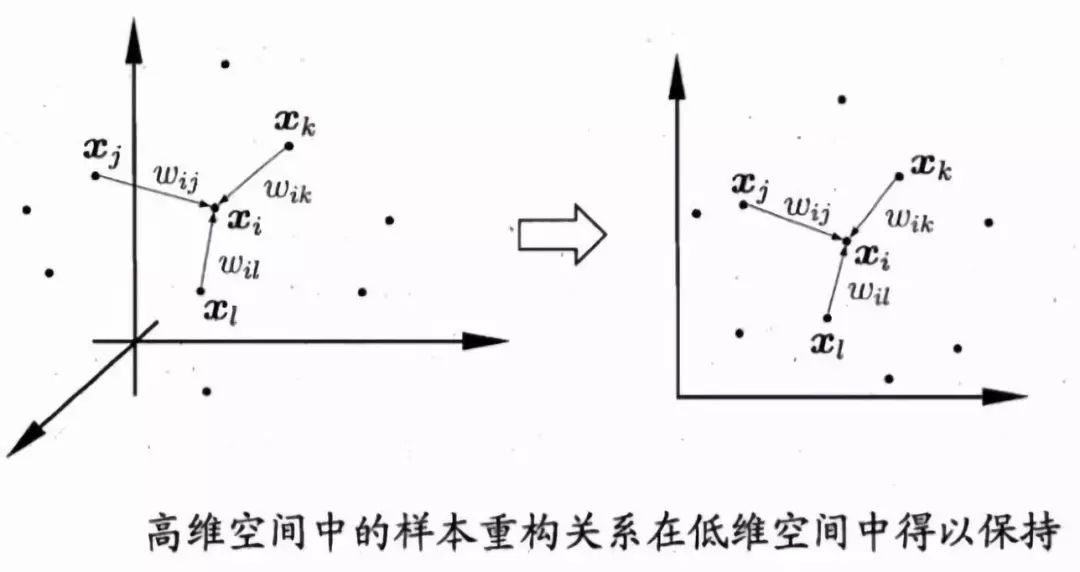
总的来说，对于不在某一个点x0邻域内的其他点A，不管A怎么变动，都不会影响到点x0，这种变动局部限制的思想在很多地方都有用，此外LLE尽可能的保存了局部线性信息，使得其在局部能反映出数据原本的结构。它的流程大致如下图所示：

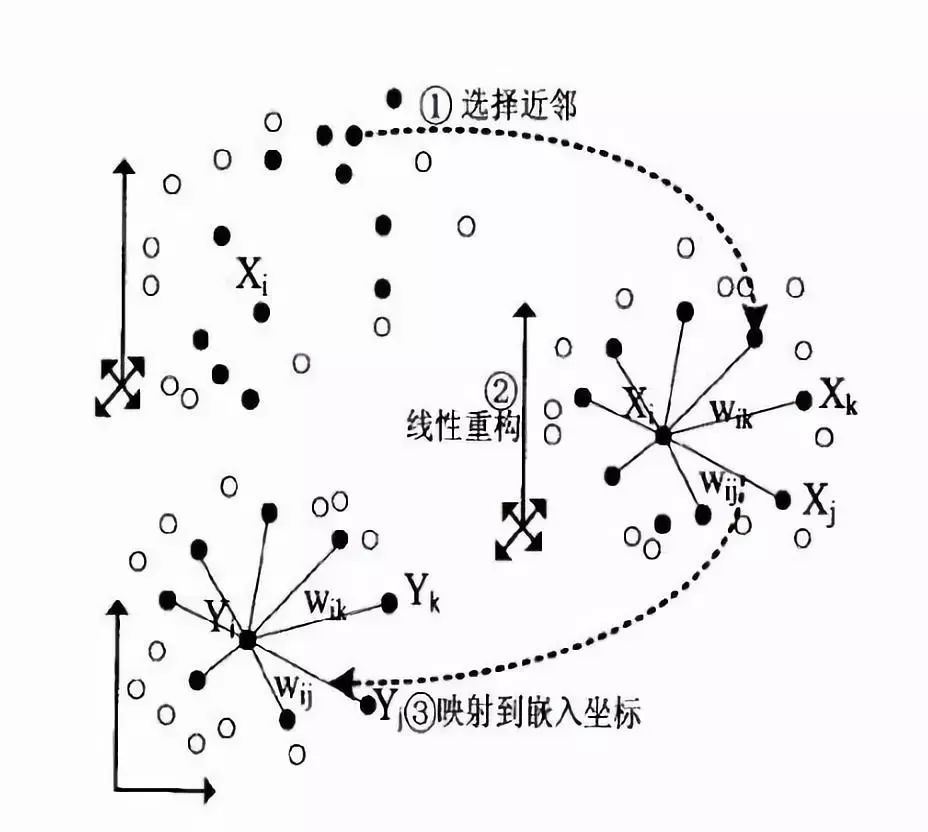
小结

LLE是广泛使用的图形图像降维方法，它实现简单，但是对数据的流形分布特征有严格的要求。比如不能是闭合流形，不能是稀疏的数据集，不能是分布不均匀的数据集等等，这限制了它的应用。

优点

1、可以学习任意维的局部线性的低维流形

2、算法归结为稀疏矩阵特征分解，计算复杂度相对较小，实现容易

缺点

1、算法所学习的流行只能是不闭合的，且样本集是稠密均匀的

2、算法对最近邻样本数的选择敏感，不同的最近邻数对最后的降维结果有很大影响