

详细分析BUCK电源的参数计算
电子说
描述
瞬态响应
小时候喜欢看赵忠祥的动物世界,有这样一幅紧张又刺激的画面一直留存在脑海里,草原上一群小鹿正在休憩着,一只豹子慢慢靠近,然后突然发力扑过去,受惊的小鹿立刻发足狂奔,反应速度快的可以逃脱,反应速度慢的就成为了豹子的大餐,这里我们先记着“反应速度”这个词。
我们在使用电脑时,当电脑处于休眠状态时按下任意一个唤醒键,电脑要能够瞬间Warm up起来,准备迎接主人的各种操作,这个过程越快越好,快到人们几乎没有感觉,这时候内部主要电源的电流会突然拉升,相应的输出电压会先Collapse然后重新建立平衡回到原点,看图1。这里我们记住“环路带宽”这个词,环路带宽越大,电压回到原点的过程就越快。
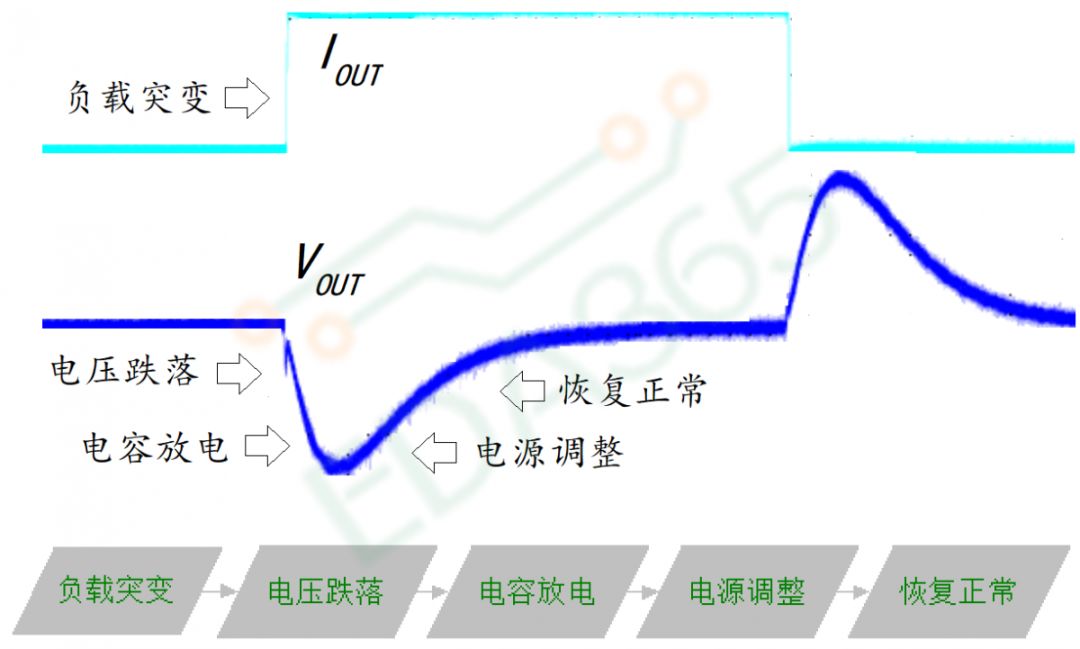
图1 瞬态响应
那么这跟上面豹子和小鹿有什么关系呢?前面小鹿的“反应速度”和后面电脑的“环路带宽”是一个概念。图2是一张二者的类比图,电源系统必须要能够从负载的突变中快速恢复正常,否则电脑就会象上面那只可怜的小鹿一样挂了。你知道吗?此时电脑内部的电源可遭罪了,因为此时系统的功耗会猛一下窜到很高,低功耗(电流)的平衡被打破,需要重新调整到高功耗的平衡。
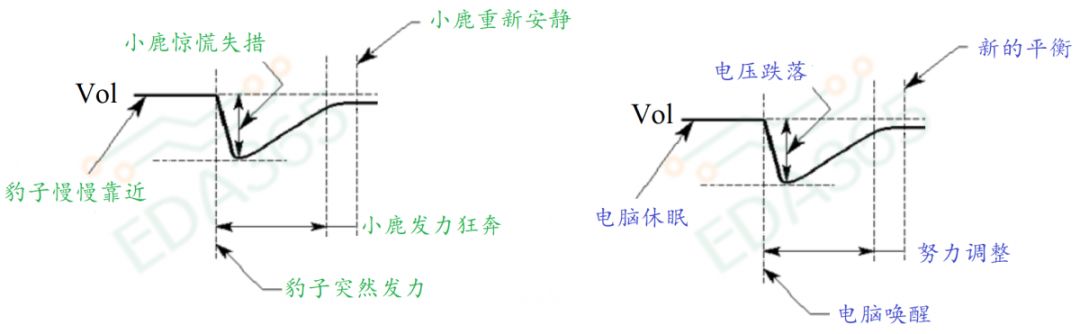
图2 电脑和小鹿的类比
当电脑唤醒或者睡眠的瞬间,板子上的DC-DC BUCK电源输出端的负载电流会发生突变,导致输出的电压产生短暂的晃动,在经过快速调整后恢复到正常电压,这种过程我们称之为电源的瞬态响应,在调整过程中需要满足三个方面的设计要求:
1. 电压调整– 输出电压的晃动不能超出芯片的工作范围;
2. 环路带宽– 输出电压恢复到正常电压的时间要尽量快;
3. 环路稳定– 输出电压在电源做调整时不能产生振铃(图2)。
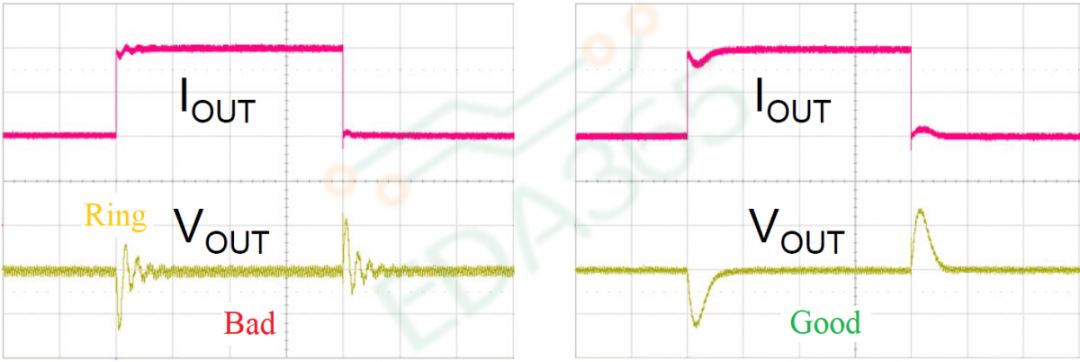
图3 振铃
01输出电容和带宽1.1瞬态电流上升
如图3左所示是一个简单的BUCK控制器示意图,我们先不对每个部分做详细的介绍,左图是输出电容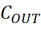 的等效电路,熟悉电源完整性知识的人会知道这是电容的实际等效模型电路。
的等效电路,熟悉电源完整性知识的人会知道这是电容的实际等效模型电路。
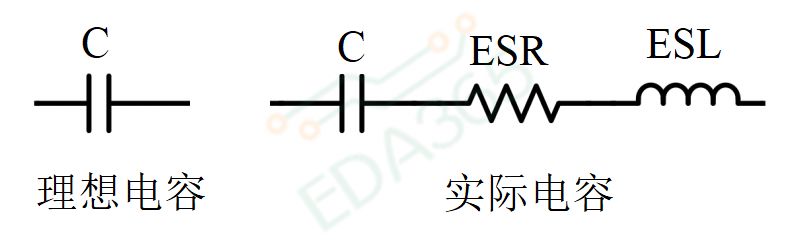
当负载发生突变时由于电源的环路需要一定的时间才能做出反应,所以只能由输出电容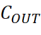 先暂时充当给负载供电的角色,这时候我们可以认为电源已经没有了,全靠电容里面存着电荷来撑着,所以从图3右我们看到输出电容上电压的变化步骤复位四步:ESR跌落→ESL Spike→电容放电→电源环路调整。
先暂时充当给负载供电的角色,这时候我们可以认为电源已经没有了,全靠电容里面存着电荷来撑着,所以从图3右我们看到输出电容上电压的变化步骤复位四步:ESR跌落→ESL Spike→电容放电→电源环路调整。
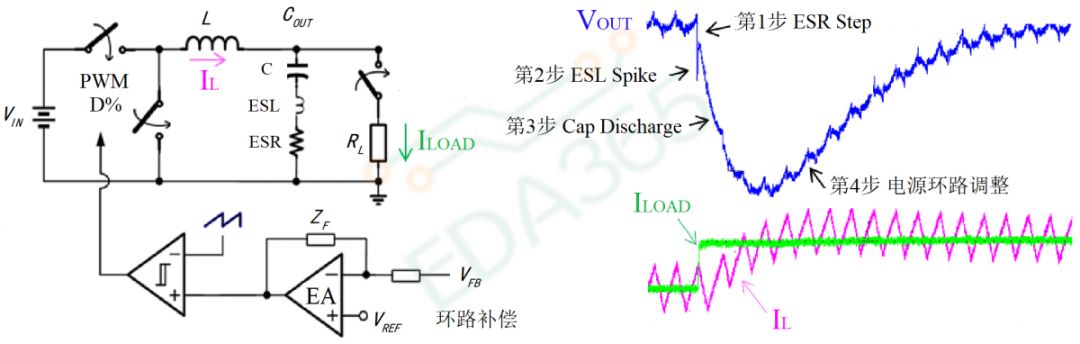
图4 瞬态响应电流上升示意图
在负载突变的瞬间,我们明白两件事情很重要:
1. 输出电容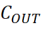 - 当负载突然变大,电源电压快速跌落,此时电源还来不及做出调整,输出电容
- 当负载突然变大,电源电压快速跌落,此时电源还来不及做出调整,输出电容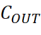 就成为了救命稻草,那么电容取多大值合适呢?越大越好吗?
就成为了救命稻草,那么电容取多大值合适呢?越大越好吗?
2. 恢复速度– 恢复速度指的就是环路带宽,带宽越大恢复速度就越快,表示电源。
要多久开始做出调整,否则光靠输出电容存储的电荷是撑不住的。
根据图5所示,我们来详细计算电源电压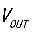 变化过程。
变化过程。
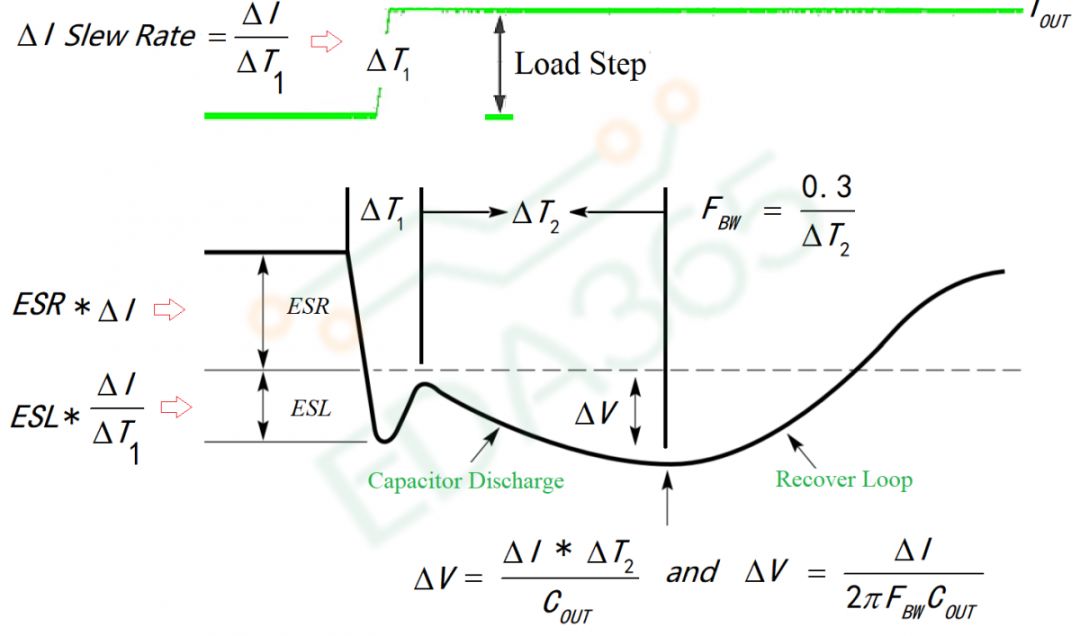
图5 输出电容和环路带宽的计算
1)第一步:输出电容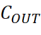 的ESR引起的直流电压跌落
的ESR引起的直流电压跌落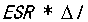
2)第二步:输出电容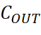 的ESL引起的交流Spike
的ESL引起的交流Spike 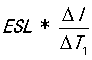 ,
,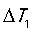 为已知;
为已知;
3)第三步:输出电容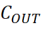 开始放电,我们要确保
开始放电,我们要确保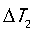 时
时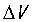 是可接受的;
是可接受的;
4)第四步:整理思路,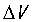 和
和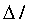 是已知的,
是已知的,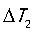 和
和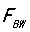 都是环路带宽
都是环路带宽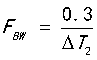
5)第五步:计算输出电容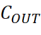 的值,方法一,
的值,方法一,
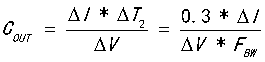
6)第六步:计算输出电容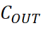 的值,方法二,
的值,方法二,
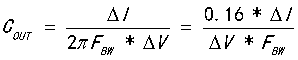
7)第七步:得出经验公式,
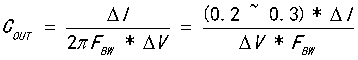
结论一:带宽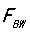
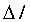
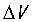
1.2负载瞬态电流下降
前面我们讨论了瞬态电流上升,这里我们接着讨论瞬态电流下降,通俗一点说就是电源的负载从最大突然拉低到最小。如图6左,假设Load突然断开,此时电感上的电流由于不能突变,会继续流向电容,电容上的电压会突然升高,同样的我们需要输出电压的Overshoot不要超过芯片的范围。
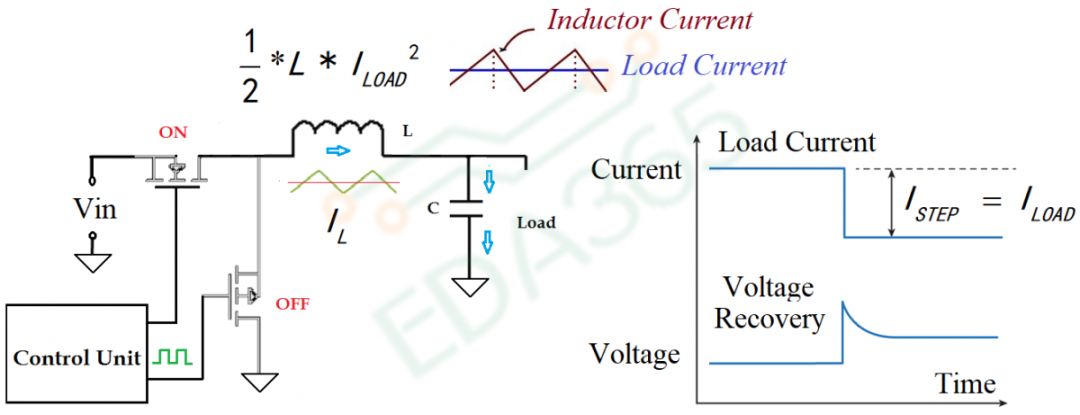
图6 负载电流由最大变最小
我们来计算电压升高的幅度:
1)当电源输出的负载电流瞬间从最大变道最小(为了计算方便,我们假定最小为0)的时候,电容存储的能量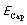 为:
为: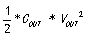
2)电感存储的能量约为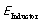 :
: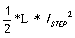
3)根据能量守恒,二者相加后的能量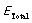 等于:
等于: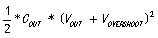
4)所以我们得到下面的三个公式:
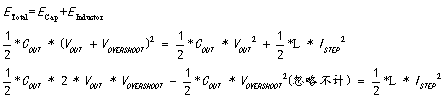
为了计算简单,其中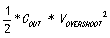 忽略不计,我们得到:
忽略不计,我们得到: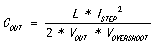
其中:
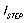 - 负载电流从最大到最小的变化量,
- 负载电流从最大到最小的变化量,
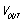 - 输出电压额定值,
- 输出电压额定值,
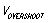 - 芯片允许的电压最大值,
- 芯片允许的电压最大值,
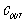 - 电源输出电容的值。
- 电源输出电容的值。
结论二:电感L,负载瞬态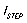
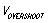
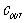
02电感
图6描述了BUCK的基本工作原理,S1和S2交替做开和关的动作,把输入端的能量传递到输出端,实现了降压的动作,也传递了电流。
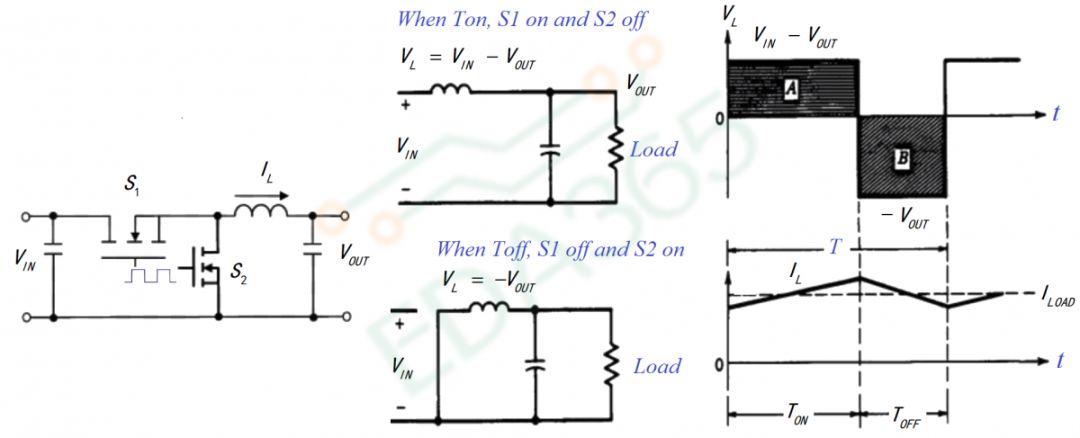
图7 BUCK工作原理
1)我们先来计算输入电压和输出电压的关系表达式,根据图6右,A的面积和B的阴影面积相等,所以有:
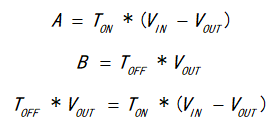
最终得出:
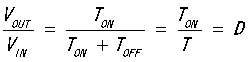
其中D为占空比。
这里有人会说,为什么A的面积和B的面积一定相等,理解不了啊,为此我用了另外一种方法:
根据电感的公式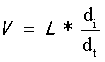 ,我们列出电感两端分别在Ton和Toff时的电压公式:
,我们列出电感两端分别在Ton和Toff时的电压公式:
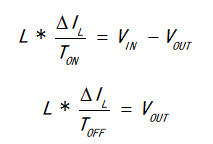
同样解这两方程,我们也能得到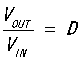 。
。
2)我们接着推导电感的计算公式,根据前面的公式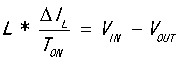 和
和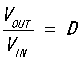
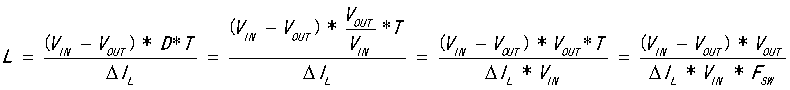
结论三:开关频率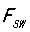 ,
,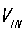 ,
,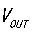 ,
,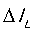 已知,就能计算出电感L的值,其中:
已知,就能计算出电感L的值,其中:
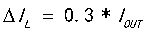 (负载电流)
(负载电流)
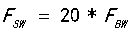 (带宽)
(带宽)
03输出电容3.1Ripple current
如图7所示,BUCK的电感上会随着Ton和Toff的来回切换产生纹波电流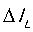 ,这个纹波电流在输出电容上会产生纹波电压
,这个纹波电流在输出电容上会产生纹波电压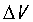 。参考图6左的电路:
。参考图6左的电路:
1. Ton - 当S1导通S2断开时,电感纹波电流上升,电容纹波电压上升;
2. Toff - 当S1断开S2导通时,电感纹波电流下降,电容纹波电压下降。
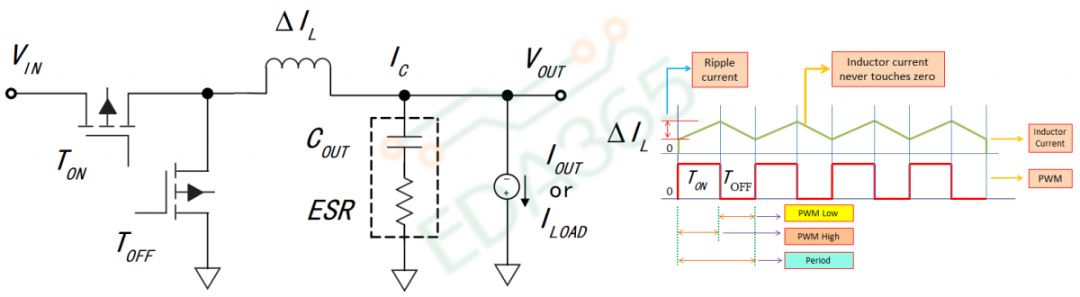
图8 纹波电流
通过纹波电流,我们来计算纹波电压,图7所示电容的纹波电压范围两个部分。
1)ESR
这个比较好算,欧姆定理就搞定啦: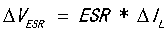
2. 输出电容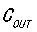
先来看纹波电流在电感和电容上的分布波形,图8所示,电感的纹波电流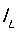 的平均值就是供给负载的电流
的平均值就是供给负载的电流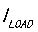 (or
(or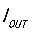 )。
)。
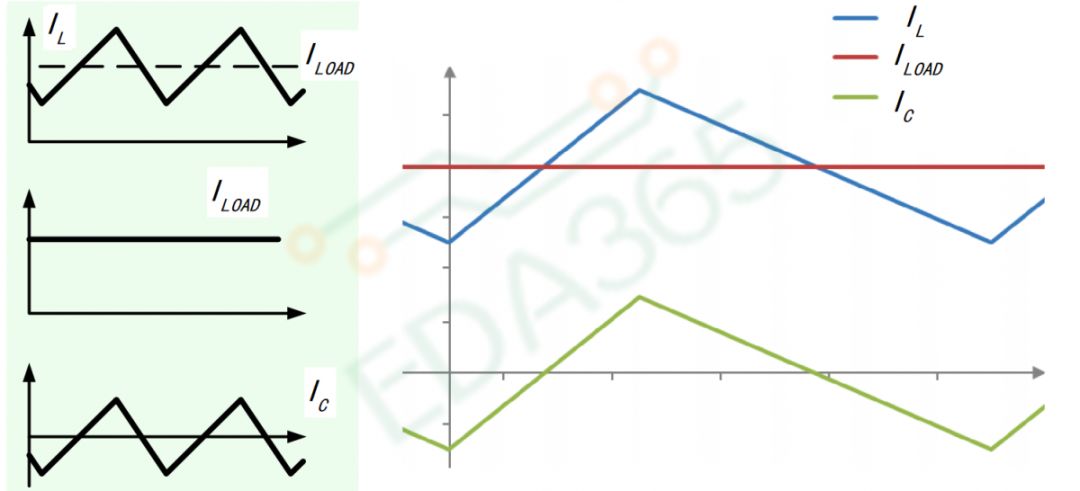
图9 纹波电流
我们在进一步细化……
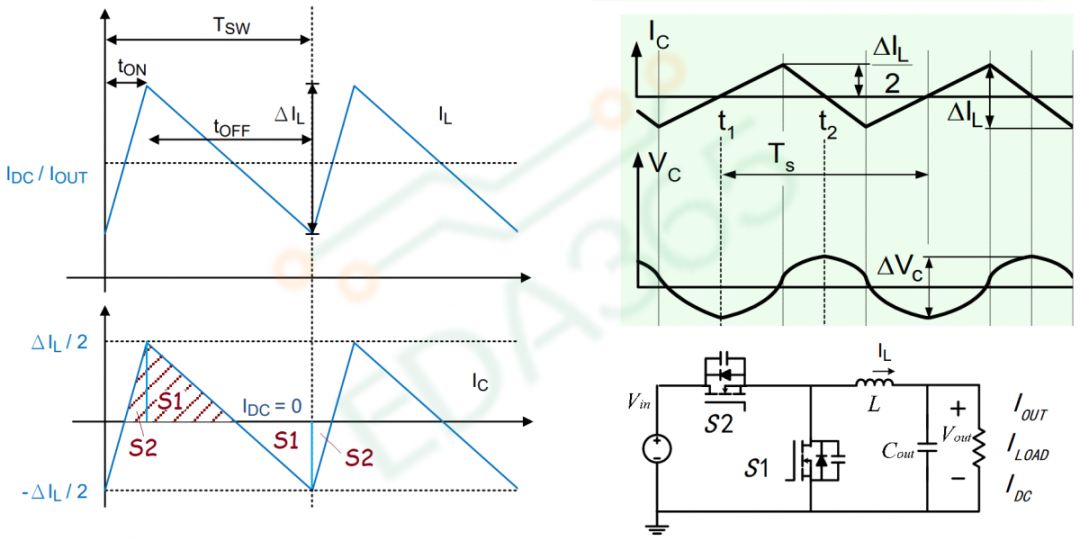
图10 纹波电压
根据图10左,当输出稳定的直流电压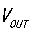 时,电容上的电流
时,电容上的电流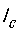 以0中心上下完全对称,也就是S1和S2区域是完全对称的结构,这样才能保证电容的充电电荷和放电电荷相等。
以0中心上下完全对称,也就是S1和S2区域是完全对称的结构,这样才能保证电容的充电电荷和放电电荷相等。
我们计算一下电荷Q = S1+S2的面积:
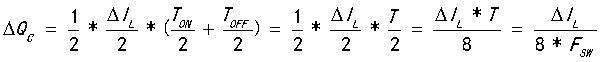
同时我们也知道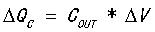
解这两个公式,我们得到: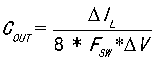
其中:
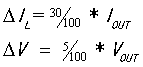
结论四:开关频率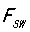 ,
,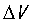 ,
,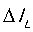 已知,就能计算出
已知,就能计算出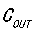 。
。
总结
结论一:带宽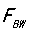 ,负载瞬态
,负载瞬态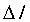 /
/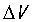 已知,就可以计算出
已知,就可以计算出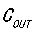
结论二:电感L,负载瞬态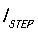 /
/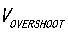 已知,就能计算出电容
已知,就能计算出电容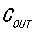
结论三:开关频率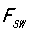 ,
,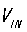 ,
,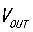 ,
,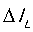 已知,就能计算出电感L的值,其中:
已知,就能计算出电感L的值,其中:
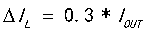 (负载电流),
(负载电流),
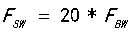 (带宽);
(带宽);
结论四:开关频率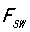 ,
,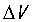 ,
,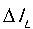 已知,就能计算出
已知,就能计算出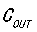
结论五: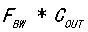 在输出负载已知的情况下是常数,输出输出电容和环路带宽成反比关系;
在输出负载已知的情况下是常数,输出输出电容和环路带宽成反比关系;
结论六:输出电感L和输出电容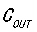 的角频率
的角频率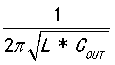 和内部补偿电路匹配到带宽
和内部补偿电路匹配到带宽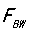
-
电源电路图最最最最最详细分析2012-07-31 18711
-
DVI接口详细分析2012-08-11 8214
-
uboot代码详细分析2016-01-29 5650
-
分析和讲解BUCK降压电源芯片方案2019-03-19 9111
-
详细分析一下USB协议2021-05-24 2027
-
详细分析stm32f10x.h2021-08-05 1289
-
详细分析了VTIM和VMIN的功能2021-11-05 1812
-
焊接技术详细分析2010-01-26 2157
-
电子整流器工作原理详细分析2010-02-27 25836
-
半桥电源源高频链逆变电路的详细分析2017-09-14 1105
-
Buck变换器原理详细分析2017-09-15 1600
-
物联网的产业生态是怎样的详细分析概述2018-12-08 5733
-
一些开关电源的拓扑结构详细分析2021-01-06 1184
-
正激有源钳位的详细分析2021-06-16 1719
-
机房托管费详细分析2025-02-28 1095
全部0条评论

快来发表一下你的评论吧 !

