从四个经典角度看机器学习的本质

何谓“机器学习”，学界尚未有统一的定义。本文摘取Tom Mitchell、Christopher M. Bishop、去年出版的《深度学习》和侧重实战的《数据挖掘》，总结了四种机器学习主流定义。更好地研究“机器学习”，并继续扩展和完善它的定义，也有助于我们理解机器学习的本质。

你或许已经读过许多关于机器学习的深度和和半深度的文章，并探讨了机器学习与众多其他主题的关系。在讨论如此复杂的概念时，回到最初的一些共同参考资料总是一个好主意；问题是，对于机器学习这样的主题，存在无数这样的参考资料。

所以我想，为什么不研究一下这些参考点呢？

这是一篇不那么严肃的帖子，旨在探讨机器学习的本质。

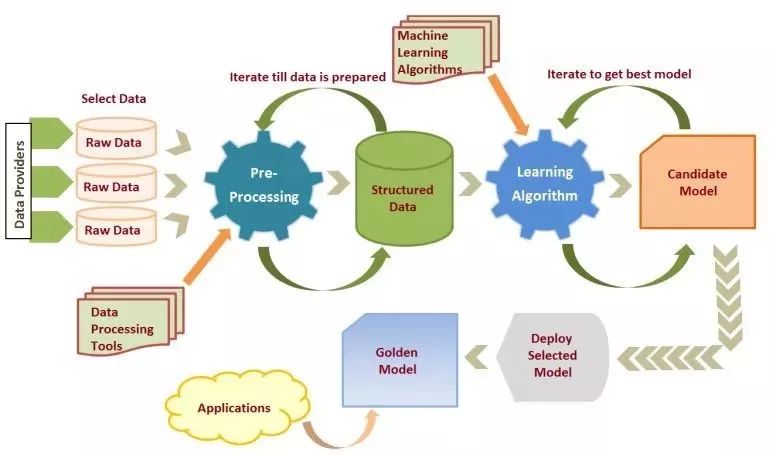
话不多说，作为一个看似属于语义学的练习，让我们来探索一下关于机器学习的定义。

Tom Mitchell：根据优化过程抽象定义机器学习

第一个定义，是我个人最喜欢的，来自著名的计算机科学家、机器学习研究者，卡内基梅隆大学的 Tom Mitchell 教授。

对于某类任务 T 和性能度量 P，如果一个计算机程序在 T 上以 P 衡量的性能随着经验 E 而自我完善，那么我们称这个计算机程序在从经验 E 中学习。[1]

Mitchell 的这个定义在机器学习领域是众所周知的，并且经受了时间的考验。这句话首次出现在他 1997 年出版的 Machine Learning 一书中。

这句话对我个人产生了很大的影响，多年来我多次提到它，并在硕士论文中引用了这个定义。在 Goodfellow, Bengio & Courville 最近出版的权威著作《深度学习》(Deep Learning) 的第 5 章中，这段引文也占据了突出位置，成为该书对学习算法的解释的出发点。

下图是 Mitchell 定义的图示：

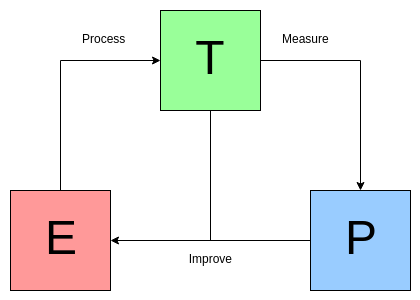
图 1：The Mitchell Paradigm

“花书”《深度学习》：论计算在机器学习中的重要性

说到 Goodfellow、Bengio 和 Courville，就不得不提他们合著的《深度学习》，这本书对机器学习是这样定义的：

机器学习本质上属于应用统计学，更多地关注如何用计算机统计地估计复杂函数，不太关注为这些函数提供置信区间。[2]

Mitchell 对机器学习的定义在应用中不再适用；它侧重于优化过程的具体组成部分，这些组成部分通常与机器学习有关，但它没有规定应该如何在实践中接近它。

《深度学习》中对机器学习的定义在本质上要规范得多，它指出计算能力得到了利用 (实际上强调了对计算能力的使用)，而传统的统计概念置信区间则不再强调。

实战数据挖掘：“学习”必须是有意地去学习

在我看来，另一个特别值得注意的关于机器学习的定义来自 Witten, Frank & Hall 所著的《数据挖掘：实用机器学习工具与技术》，这是我第一本完整阅读了的关于这个主题的书。

《数据挖掘》这本书很少涉及数学，但有很多实用性的解释。对于刚进入机器学习领域的人，“数据挖掘” 很长一段时间是我的首选推荐。

作者对机器学习最初定义有点零散，他们试图在机器学习和数据挖掘的背景中将学习、性能和知识这些概念编织在一起。但其中一些语句值得注意：

我们感兴趣的是在新的情况下得到性能的改进，或至少有性能改进的潜力。

当系统以一种使它们在未来表现更好的方式改变自己的行为时，它们就会学习。

学习意味着思考和目标。学习必须是有意地去学习。

经验表明，在机器学习和数据挖掘的许多应用中，所获得的显式知识结构、结构描述，至少与在新实例中表现良好的能力同等重要。人们经常使用数据挖掘来获取知识，而不仅仅是用来预测。

“数据挖掘”这个术语被用作机器学习的补充术语。上面引用的语句出自这本书的第三版，出版于 2011 年，当时数据挖掘这个词比现在更有吸引力；即使不说是引用自数据挖掘的书，上面所写的内容对机器学习本身也适用。

Witten, Frank & Hall 为机器学习的定义提供了一个不同的角度：Mitchell 专注于优化过程的特定组成部分，Goodfellow, Bengio & Courville 倾向于一种更规范的定义，并强调计算能力的相对重要性，这个定义则尝试侧重 “learning” 的哪些方面在机器学习过程中是类似和重要的。

上面引用的语句还提供了一个重要的点，兼具实用性和哲学性，即最后一段，指出获得知识和使用这些知识的能力都是机器学习的重要方面。

Christopher Bishop：从算法的角度定义

最后，让我们来看 Christopher Bishop 在《模式识别和机器学习》一书中对机器学习的定义。值得注意的是，Bishop 没有开门见山地定义这个术语，但是很好地隐式地提供了以算法为中心的机器学习的定义 (在一个数字分类任务中讨论到)：

机器学习算法的结果表示为一个函数 y (x)，它以一个新的数字的图像 x 作为为输入，产生向量 y，与 target vector 的形式相同。

函数 y (x) 的精确形式是在训练阶段 (training phase) 确定的，也称为学习阶段 (learning phase)，以训练数据为基础。

一旦模型被训练出来，就可以用来判断新的数字图像 (新样本) 对应的标签，这些新样本的集合被称为测试集。

正确分类与训练集不同的新样本的能力叫做泛化 (generalization)。在实际应用中，输入向量的可变性使得训练数据只能包含所有可能输入向量的很小一部分，因此泛化是模式识别的一个中心目标。[4]

首先，除了我们讨论的机器学习是有监督学习，而不是无监督学习或强化学习 (或其他形式的机器学习) 外，上面的引用对 “模式识别” 没有更多的解释。

其次，也是更重要的一点，这是唯一对机器学习所需步骤逐步处理的定义，无论这些步骤在这个例子中可能多么简短。

同样有趣的是，随后的页面，以及 Bishop 的书一半的篇幅概述了许多额外的机器学习概念，并将它们很好地结合在一起，提供了具有可读性的介绍，而不至于陷入数学的困境 (书中的其余部分解释了数学)。 

这样，我们已经有四种方法来定义机器学习：一种是根据它的优化过程，抽象地定义它机器学习；第二种更有规范性，并指出计算在机器学习中的重要性；第三定义侧重于 “学习” 的哪些方面在机器学习过程中是类似的和重要的；最后一个定义从算法的角度概述了机器学习。

这些定义都不是不正确，但都不完整。探讨先驱者和受人尊敬的研究人员所认为的 “机器学习”，将扩展我们自己对机器学习的定义。