

ICLR-17最佳论文《理解深度学习需要重新思考泛化》
电子说
描述
ICLR-17最佳论文《理解深度学习需要重新思考泛化》曾引发学界热议。现作者张驰原和Samy Bengio等再出新作,指出神经网络每个层并非“生而平等”,进一步拓展对神经网络泛化的理解。
今天新智元要介绍的论文是ICLR 2017最佳论文奖得主、《理解深度学习需要重新思考泛化》的作者张弛原和Samy Bengio等人的新作:
神经网络的各个层生而平等吗?(Are All Layers Created Equal?)

张弛原、Samy Bengio等人新作:神经网络各个层生而平等吗?
在ICLR 2017那篇“重新思考泛化”的文章中,张驰原等人得出结论认为,只要参数的数量超过实践中通常的数据点的数量,即便是简单的层数为2的神经网络,就已经具有完美的有限样本表现力(finite sample expressivity)。
而在这篇新的论文中,张弛原等人继续探讨深度神经网络的泛化能力,深入到“层”的级别,并指出在研究深度模型时,仅关注参数或范数(norm)的数量是远远不够的。
研究深度模型时,只考虑参数和范数的数量是不够的
理解深层架构的学习和泛化能力是近年来一个重要的研究目标,《理解深度学习需要重新思考泛化》发表后在学界卷起了一股风暴,有人甚至称其为“势必颠覆我们对深度学习理解”。

ICLR 2017最佳论文《理解深度学习需要重新思考泛化》
ICLR 2017那篇文章指出,传统方法无法解释大规模神经网络在实践中泛化性能好的原因,并提出了两个新的定义——“显示正则化”和“隐示正则化”来讨论深度学习。
作者通过在CIFAR10和ImageNet的几个不同实验发现:
神经网络的有效容量对于整个数据集的暴力记忆是足够大的;
对随机标签进行优化的过程很容易。与对真实标签的训练相比,随机标签的训练时间只增加了一个小的恒定因子;
对标签进行随机化只是一种数据变换,神经网络要学习的问题的所有其他属性不变。
更准确地说,当对真实数据的完全随机标记进行训练时,神经网络实现了零训练误差——当然,测试误差并不比随机概率好,因为训练标签和测试标签之间没有相关性。
换句话说,通过单独使标签随机化,我们可以迫使模型的泛化能力显著提升,而不改变模型、大小、超参数或优化器。
这一次,论文又提出了两个新的概念——(训练后)“重新初始化”和“重新随机化鲁棒性”,并认为神经网络的层可以分为“关键层”和“鲁棒层”;与关键层相比,将鲁棒层重置为其初始值没有负面影响,而且在许多情况下,鲁棒层在整个训练过程中几乎没有变化。
作者根据经验研究了过度参数化深度模型的分层功能结构,为神经网络层的异构特征提供了证据。
再次思考神经网络泛化:各个层并非“生而平等”
深度神经网络在现实世界的机器学习实例中已经得到了非常成功的应用。在将这一系统应用于许多关键领域时,对系统的深层理解至少与其最先进的性能同样重要。最近,关于理解为什么深度网络在实践中表现优异的研究主要集中在网络在漂移下的表现,甚至是数据分布等问题上。
与此类研究相关的另一个有趣的研究是,我们如何解释并理解受过训练的网络的决策函数。虽然本文的研究问题与此相关,但采取了不同的角度,我们主要关注网络层在受过训练的网络中的作用,然后将经验结果与泛化、鲁棒性等属性联系起来。
本文对神经网络表达力的理论进行了深入研究。众所周知,具有足够宽的单个隐藏层的神经网络是紧凑域上的连续函数的通用逼近器。
最近的研究进一步探讨了深度网络的表达能力,是否真的优于具有相同数量的单元或边缘的浅层网络。同时,也广泛讨论了用有限数量的样本表示任意函数的能力。
然而,在上述用于构建近似于特定功能的网络的研究中,使用的网络结构通常是“人工的”,且不太可能通过基于梯度的学习算法获得。我们重点关注的是实证深层网络架构中不同网络层发挥的作用,网络采用基于梯度的训练。
深度神经网络的泛化研究引起了很多人的兴趣。由于大神经网络无法在训练集上实现随机标记,这使得在假设空间上基于均匀收敛来应用经典学习的理论结果变得困难。
本文提供了进一步的经验证据,并进行了可能更细致的分析。尤其是,我们凭经验表明,深层网络中的层在表示预测函数时所起的作用并不均等。某些层对于产生良好的预测结果至关重要,而其他层对于在训练中分配其参数则具备相当高的鲁棒性。
此外,取决于网络的容量和目标函数的不同复杂度,基于梯度的训练网络可以不使用过剩容量来保持网络的复杂度。本文讨论了对“泛化“这一概念的确切定义和涵盖范围。
全连接层(FCN)
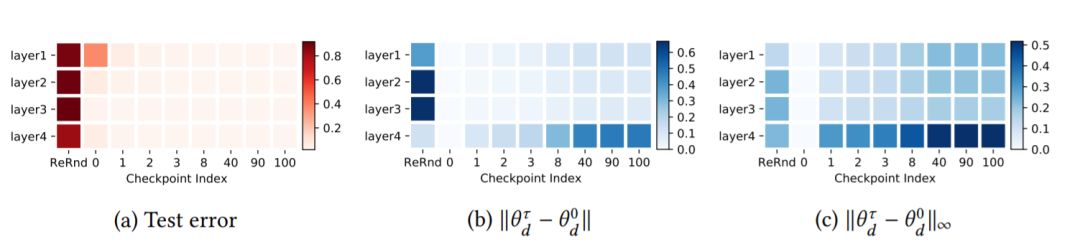
图1:MNIST数据集上FCN 3×256的鲁棒性结果。(a)测试错误率:图中每行对应于网络中的每一层。第一列指定每个层的鲁棒性w.r.t重新随机化,其余列指定不同检查点的重新初始化鲁棒性。最后一列为最终性能(在训练期间设置的最后一个检查点)作为参考。(b-c)权重距离:热图中的每个单元表示训练参数与其初始权重的标准化2范数(b)或∞范数(c)距离
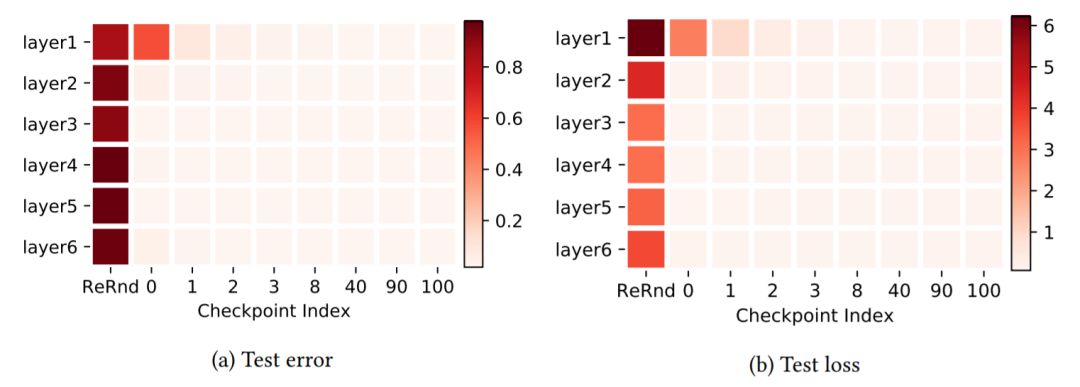
图2:MNIST数据集上FCN 5×256的层鲁棒性研究。两个子图使用与图1(a)相同的布局。两个子图分别表示在测试错误(默认值)和测试损失中评估的鲁棒性
大规模卷积网络(CNN)
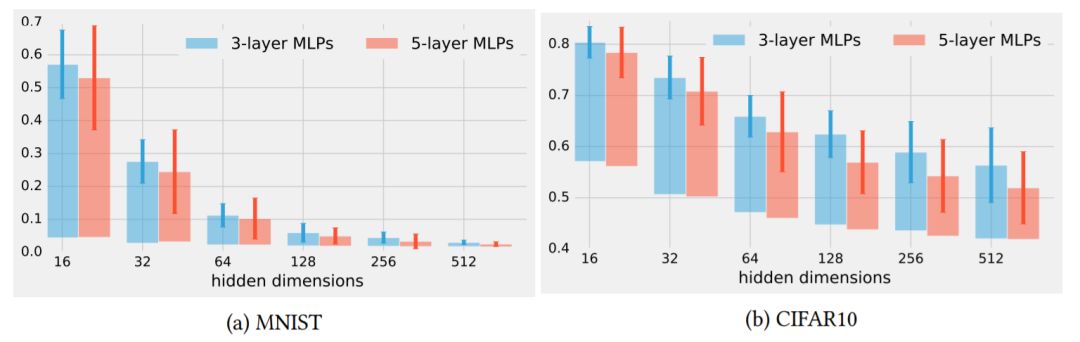
图3:重新初始化所有层的鲁棒性,但第一次使用检查点0用于不同维度的隐藏层的FCN。每个条形表示完全训练后的模型有具有一层重新初始化的模型之间的分类误差的差异。误差条表示通过使用不同的随机初始化运行实验得到的一个标准偏差。
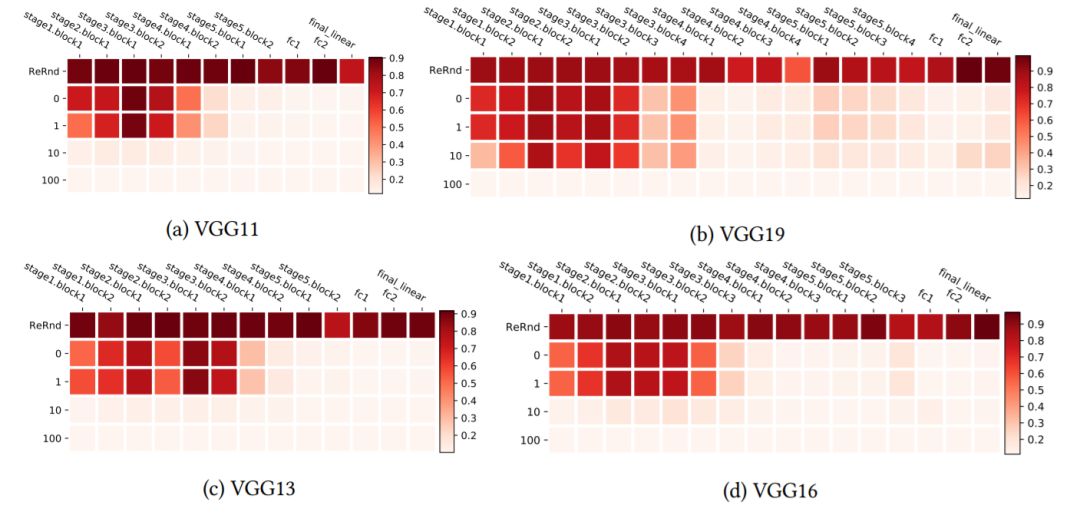
图4:使用CIFAR10上的VGG网络进行分层鲁棒性分析。热图使用与图1中相同的布局,但加以转置,以便更有效地对更深层的架构进行可视化。
残差网络(ResNets)
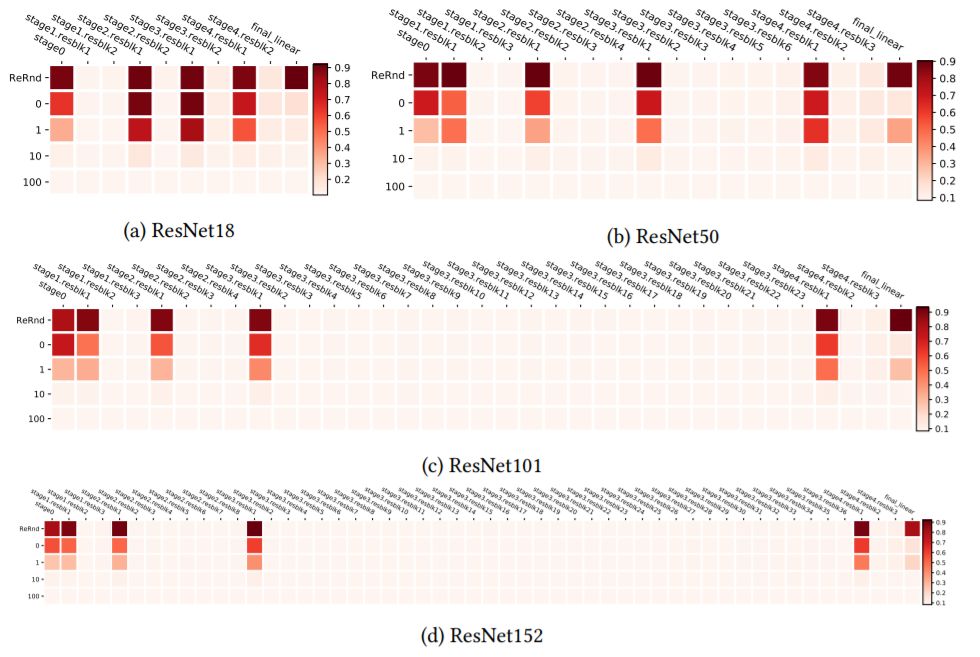
图5:在CIFAR10上训练的ResNets残差块的分层鲁棒性分析。

图6:在ImageNet上训练的ResNets残差块的分层鲁棒性分析

图7:采用/不采用下采样跳过分支的残余块(来自ResNets V2)。C,N和R分别代表卷积、(批量)归一化和ReLU激活
网络层的联合鲁棒性

图8:MNIST上FCN 5×256的联合鲁棒性分析。布局与图1中的相同,但是图层分为两组(每个图层中图层名称上的*标记表示),对每组中的所有图层全部应用重新随机化和重新初始化。

图9:CIFAR10上ResNets的联合鲁棒性分析,基于对所有剩余阶段中除第一个残余块之外的所有剩余块进行分组的方案。分组由图层名称上的*表示。
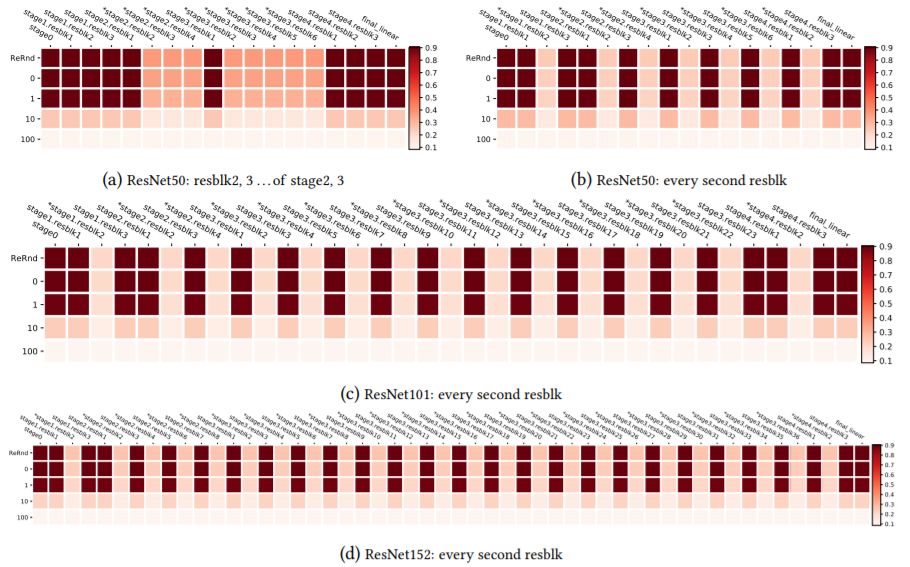
图10:CIFAR10上ResNets的联合鲁棒性分析,以及其他分组方案。分组由图层名称上的*表示
-
ICLR 2019论文解读:深度学习应用于复杂系统控制2019-01-10 8550
-
谷歌工程师机器学习干货:从表现力、可训练性和泛化三方面详解2017-11-26 5744
-
谷歌工程师浅谈Bengio深度学习论文的重要性2018-01-06 1171
-
深度学习如何确定最佳深度?2018-04-04 5656
-
探索机器“视觉”演进的无限可能性 Qualcomm AI研究人员获得ICLR殊荣2018-05-10 5702
-
ICLR 2019在官网公布了最佳论文奖!2019-05-07 4946
-
ICLR 2019最佳论文日前揭晓 微软与麻省等获最佳论文奖项2019-05-11 2797
-
谷歌发表论文EfficientNet 重新思考CNN模型缩放2019-06-03 7128
-
泛在电力物联网的发展真的需要5G吗2019-07-12 1253
-
自监督学习与Transformer相关论文2020-11-02 3161
-
如何理解泛化是深度学习领域尚未解决的基础问题2021-04-08 3161
-
基于深度学习的评论文本推荐方法2021-06-09 818
-
基于评分矩阵与评论文本的深度学习模型2021-06-24 860
-
深度学习顶级学术会议ICLR 2023录用结果已经公布!2023-02-07 2707
-
PyTorch教程5.5之深度学习中的泛化2023-06-05 519
全部0条评论

快来发表一下你的评论吧 !

