对scikit-learn和numpy生成数据样本的方法做一个总结

‍‍‍‍在学习机器学习算法的过程中，我们经常需要数据来验证算法，调试参数。但是找到一组十分合适某种特定算法类型的数据样本却不那么容易。还好numpy, scikit-learn都提供了随机数据生成的功能，我们可以自己生成适合某一种模型的数据，用随机数据来做清洗，归一化，转换，然后选择模型与算法做拟合和预测。

1. numpy随机数据生成API‍‍‍‍

numpy比较适合用来生产一些简单的抽样数据。API都在random类中，常见的API有：

1) rand(d0, d1, ..., dn) 用来生成d0×d1×...dn维的数组 。数组的值在[0,1)之间

例如: np.random.rand(3,2,2)，输出如下3×2×2的数组

array([[[ 0.49042678,  0.60643763],        [ 0.18370487,  0.10836908]],       [[ 0.38269728,  0.66130293],        [ 0.5775944 ,  0.52354981]],

[[ 0.71705929,  0.89453574],        [ 0.36245334,  0.37545211]]])

2) randn((d0, d1, ..., dn) 也是用来生成d0xd1x...dn维的数组。不过数组的值服从N(0,1)的标准正态分布。

例如：np.random.randn(3,2)，输出如下3x2的数组，这些值是N(0,1)的抽样数据。

array([[-0.5889483 , -0.34054626],       [-2.03094528, -0.21205145],       [-0.20804811, -0.97289898]])

如果需要服从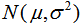的正态分布，只需要在randn上每个生成的值x上做变换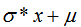即可 。

例如: 2*np.random.randn(3,2) + 1，输出如下3x2的数组，这些值是N(1,4)的抽样数据。

array([[ 2.32910328, -0.677016  ],       [-0.09049511,  1.04687598],       [ 2.13493001,  3.30025852]])

3) randint(low[, high, size])，生成随机的大小为size的数据，size可以为整数，为矩阵维数，或者张量的维数。值位于半开区间 [low, high)。

例如:np.random.randint(3, size=[2,3,4])返回维数维2x3x4的数据，取值范围为最大值为3的整数。

array([[[2, 1, 2, 1],　　　　　　　　　　[0, 1, 2, 1],　　　　　　　　　　[2, 1, 0, 2]],　　　　　　　　　　[[0, 1, 0, 0],　　　　　　　　　　[1, 1, 2, 1],　　　　　　　　　　[1, 0, 1, 2]]])

再比如: np.random.randint(3, 6, size=[2,3]) 返回维数为2x3的数据。取值范围为[3,6).

array([[4, 5, 3],　　　　　　　　                                [3, 4, 5]])

4) random_integers(low[, high, size])，和上面的randint类似，区别在于取值范围是闭区间[low, high]。

5) random_sample([size])，返回随机的浮点数，在半开区间 [0.0, 1.0)。如果是其他区间[a,b)，可以加以转换(b - a) * random_sample([size]) + a

例如： (5-2)*np.random.random_sample(3)+2 返回[2,5)之间的3个随机数。

array([ 2.87037573,  4.33790491,  2.1662832 ]) 

2. scikit-learn随机数据生成API介绍

scikit-learn生成随机数据的API都在datasets类之中，和numpy比起来，可以用来生成适合特定机器学习模型的数据。常用的API有：

1) 用make_regression生成回归模型的数据

2) 用make_hastie_10_2，make_classification或者make_multilabel_classification生成分类模型数据

3) 用make_blobs生成聚类模型数据

4) 用make_gaussian_quantiles生成分组多维正态分布的数据

3. scikit-learn随机数据生成实例

3.1 回归模型随机数据

这里我们使用make_regression生成回归模型数据。几个关键参数有n_samples（生成样本数）， n_features（样本特征数），noise（样本随机噪音）和coef（是否返回回归系数）。例子代码如下：

import numpy as npimport matplotlib.pyplot as pltfrom sklearn.datasets.samples_generator import make_regression # X为样本特征，y为样本输出， coef为回归系数，共1000个样本，每个样本1个特征X, y, coef =make_regression(n_samples=1000, n_features=1,noise=10, coef=True)# 画图plt.scatter(X, y,  color='black')plt.plot(X, X*coef, color='blue',linewidth=3)plt.xticks(())plt.yticks(())plt.show()

输出的图如下：

3.2 分类模型随机数据

这里我们用make_classification生成三元分类模型数据。几个关键参数有n_samples（生成样本数）， n_features（样本特征数）， n_redundant（冗余特征数）和n_classes（输出的类别数），例子代码如下：

import numpy as npimport matplotlib.pyplot as pltfrom sklearn.datasets.samples_generator import make_classification # X1为样本特征，Y1为样本类别输出， 共400个样本，每个样本2个特征，输出有3个类别，没有冗余特征，每个类别一个簇X1, Y1 = make_classification(n_samples=400, n_features=2, n_redundant=0,                             n_clusters_per_class=1, n_classes=3)plt.scatter(X1[:, 0], X1[:, 1], marker='o', c=Y1)plt.show()

输出的图如下：

3.3 聚类模型随机数据

这里我们用make_blobs生成聚类模型数据。几个关键参数有n_samples（生成样本数）， n_features（样本特征数），centers(簇中心的个数或者自定义的簇中心) 和 cluster_std（簇数据方差，代表簇的聚合程度）。例子如下：

import numpy as npimport matplotlib.pyplot as pltfrom sklearn.datasets.samples_generator import make_blobs # X为样本特征，Y为样本簇类别， 共1000个样本，每个样本2个特征，共3个簇，簇中心在[-1,-1], [1,1], [2,2]， 簇方差分别为[0.4, 0.5, 0.2]X, y = make_blobs(n_samples=1000, n_features=2, centers=[[-1,-1], [1,1], [2,2]], cluster_std=[0.4, 0.5, 0.2])plt.scatter(X[:, 0], X[:, 1], marker='o', c=y)plt.show()

输出的图如下：

3.4 分组正态分布混合数据

我们用make_gaussian_quantiles生成分组多维正态分布的数据。几个关键参数有n_samples（生成样本数）， n_features（正态分布的维数），mean（特征均值），cov（样本协方差的系数）， n_classes（数据在正态分布中按分位数分配的组数）。 例子如下：

import numpy as npimport matplotlib.pyplot as pltfrom sklearn.datasets import make_gaussian_quantiles#生成2维正态分布，生成的数据按分位数分成3组，1000个样本,2个样本特征均值为1和2，协方差系数为2X1, Y1 = make_gaussian_quantiles(n_samples=1000, n_features=2, n_classes=3, mean=[1,2],cov=2)plt.scatter(X1[:, 0], X1[:, 1], marker='o', c=Y1)

输出图如下：

以上就是生产随机数据的一个总结，希望可以帮到学习机器学习算法的朋友们。