

如何用Python实现极大似然估计?
描述
极大似然估计(Maximum likelihood estimation, 简称MLE)是很常用的参数估计方法,极大似然原理的直观想法是,一个随机试验如有若干个可能的结果A,B,C,... ,若在一次试验中,结果A出现了,那么可以认为实验条件对A的出现有利,也即出现的概率P(A)较大。也就是说,如果已知某个随机样本满足某种概率分布,但是其中具体的参数不清楚,参数估计就是通过若干次试验,观察其结果,利用结果推出参数的大概值。极大似然估计是建立在这样的思想上:已知某个参数能使这个样本出现的概率最大,我们当然不会再去选择其他小概率的样本,所以干脆就把这个参数作为估计的真实值(请参见“百度百科”)。
本文以一个简单的离散型分布的例子,模拟投掷硬币估计头像(head)向上的概率。投掷硬币落到地面后,不是head向上就是tail朝上,这是一个典型的伯努利实验,形成一个伯努利分布,有着如下的离散概率分布函数:
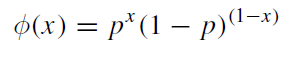
其中,x等于1或者0,即结果,这里用1表示head、0表示tail。
对于n次独立的投掷,很容易写出其似然函数:
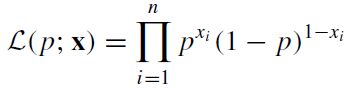
现在想用极大似然估计的方法把p估计出来。就是使得上面这个似然函数取极大值的情况下的p的取值,就是要估计的参数。
首先用Python把投掷硬币模拟出来:
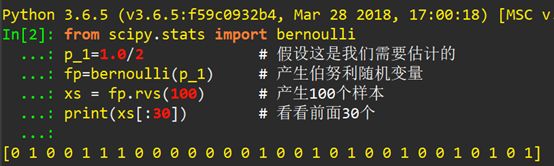
通过此模拟,使用sympy库把似然函数写出来:

从上面的结论可以看出,作100次伯努利实验,出现positive、1及head的数目是53个,相应的0也就是tail的数目是47个,比较接近我们设的初始值0.5即1.0/2(注意:现在我们假设p是未知的,要去估计它,看它经过Python的极大似然估计是不是0.5!)。
下面,我们使用Python求解这个似然函数取极大值时的p值:
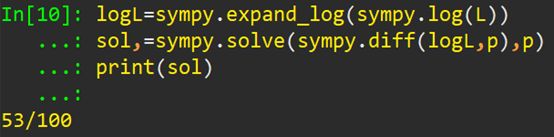
结果没有什么悬念,53/100的值很接近0.5!
取对数后,上面Python的算法最后实际上是求解下式为0的p值:
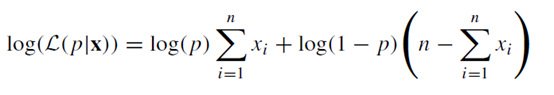
上式留给网友自行推导,很多资料都可找到该式。这个式子,是著名的Logistic回归参数估计的极大似然估计算法的基础。
进一步,为了更加直观的理解投掷硬币的伯努利实验,我们给出以均值(均值为100*0.5=50)为中心对称的加总离散概率(概率质量函数(probability mass function),Python里面使用pmf函数计算):
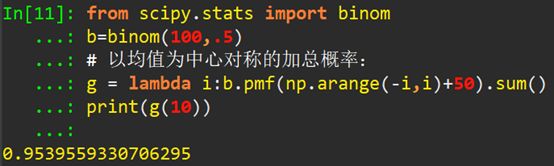
对于上面的Python代码,可以通过下图更好地去理解:
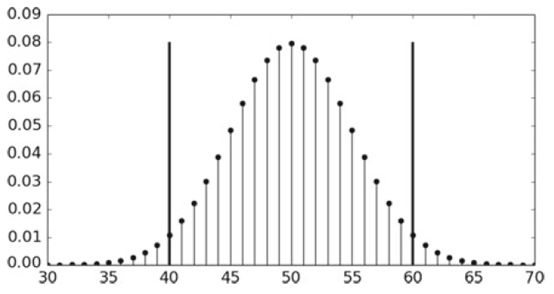
把这20个离散的概率全部显示出来,也可以看到在0.08左右取到它们的最大值:
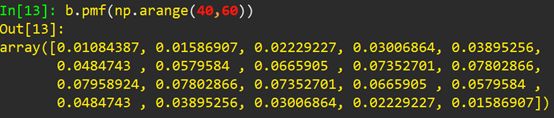
本文针对简单的离散概率质量函数的分布使用Python进行了极大似然估计,同时该方法可以应用于连续分布的情形,只要通过其概率密度函数得出其似然函数即可。希望网友把本文的代码实践一遍,也可以和R语言、SAS等软件得到的结论相比较,从而得到更好的极大似然估计的实现方法。
-
[7.2]--极大似然估计jf_75936199 2023-01-21
-
[7.4.1]--极大似然估计jf_90840116 2023-02-22
-
极大似然估计(1)#机器学习未来加油dz 2023-07-14
-
极大似然参数辨识方法2017-08-13 2430
-
巴斯卡分布中未知参数的估计2009-03-08 1344
-
多传感器的极大似然配准算法研究2009-07-10 432
-
基于极大似然法的椒盐噪声滤波算法2009-08-04 653
-
基于正交训练序列的MIMO系统联合最大似然时频同步和信道估计2010-03-06 654
-
【智能控制】极大似然参数辨识方法2017-08-07 855
-
基于极大似然的非监督噪声功率谱估计方法2018-03-07 985
全部0条评论

快来发表一下你的评论吧 !

