

ML算法工程师面试指南,完整的面试知识点、编程题及题解
电子说
描述
春季到来,春招不久也会开始。在本项目中,作者为大家准备了 ML 算法工程师面试指南,它提供了完整的面试知识点、编程题及题解、各科技公司的面试题锦等内容。目前该 GitHub 项目已经有 1 万+的收藏量,想要跳一跳的同学快来试试吧。
项目地址:https://github.com/imhuay/Algorithm_Interview_Notes-Chinese
如下所示为整个项目的结构,其中从机器学习到数学主要提供的是笔记与面试知识点,读者可回顾整体的知识架构。后面从算法到笔试面经主要提供的是问题及解答方案,根据它们可以提升整体的解题水平与编程技巧。

面试知识点
面试题多种多样,但机器学习知识就那么多,那么为了春招或春季跳槽,何不过一遍 ML 核心知识点?在这个 GitHub 项目中,作者前一部分主要介绍了机器学习及各子领域的知识点。其中每一个知识点都只提供最核心的概念,如果读者遇到不熟悉的算法或者遇到知识漏洞,可以进一步阅读相关文献。
项目主要从机器学习、深度学习、自然语言处理和数学等方面提供详细的知识点,因为作者比较关注 NLP,所以并没有提供详细的计算机视觉笔记。
机器学习
首先对于机器学习,项目主要从基础概念、基本实践、基本算法和集成学习专题这四个方面概括 ML 的总体情况。其中基础概念可能是最基本的面试问题,例如「偏差方差怎么权衡?」、「生成模型和判别模型的差别是什么?」、「先验和后验概率都是什么,它们能转换吗?」。
这些知识点一般是入门者都需要了解的,而对于 ML 基本实践,主要会从如何做好传统 ML 开发流程的角度提问。例如「你如何选择超参数,能介绍一些超参数的基本搜索方法吗?」、「混淆矩阵、准确率、精确率、召回率或 F1 值都是什么,如何使用它们度量模型的好坏?」、「你能介绍数据清洗和数据预处理的主要流程吗,举个例子?」。
这些问题都能在前两部分的知识点中找到答案。后一部分的基本算法就非常多了,从最简单的 Logistic 回归到复杂的梯度提升树,这一部分总结了主流的机器学习算法:
信息论
逻辑斯蒂回归
支持向量机
决策树
集成学习
梯度提升决策树 GBDT
随机森林
其中每一种算法都提供了最核心的概念,例如对于决策树中的 CART 算法,笔记主要引用了李航《统计学习方法》中的描述:

最后机器学习还有一个关于集成方法的专题。除了支持向量机,集成方法相关的问题在 ML 中也比较重要,因为像 XGboost 和随机森林等方法在传统 ML 中效果应该是顶尖的,被问到的概率也大得多。

深度学习
深度学习的内容就相对比较多了,目前也有非常多的笔记或资料,但是我们可能会感觉深度学习的问题并没有机器学习难。顶多会让我们手推一个反向传播算法,不会像手推支持向量机那样让我们从表达式推一下卷积网络。如果要为深度学习打基础,其实最好的办法是学习 Ian Goodfellow 的《Deep Learning》,我们只要阅读这本书的前两部分:应用数学与机器学习基础;深度网络:现代实践。第三部分因为涉及大量前沿研究的东西,我们暂时可以不急着学。
该项目主要从以下几个方面介绍深度学习面试知识点:
深度学习基础
深度学习实践
CNN 专题
RNN 专题
优化算法专题
序列建模专题
《Deep Learning》整理
前面 6 个专题都是介绍的笔记,每一个专题都有非常多的具体内容,其中序列建模专题还引用了机器之心综述的从循环到卷积,探索序列建模的奥秘。如下展示了优化算法专题所包含的内容:

在最后的《Deep Learning》整理中,项目作者给出了五十多道深度学习问题,并根据这些问题介绍《Deep Learning》中的知识点。如下为问题示例,不同的星号表示问题的难度:

自然语言处理与数学
后面的自然语言处理也是最近在重点更新的,目前介绍的方面主要有;
自然语言处理基础
NLP 发展趋势
词嵌入专题
句嵌入专题
多模态专题
视觉问答综述
深度理解查询
NLP 很多知识点其实都不算基础内容,这需要根据我们自己学习的领域收集复习内容。不过像 NLP 基础或词嵌入等知识点,项目作者介绍得很详细,它们也是 NLP 面试必备知识。
最后还有一些数学知识点,它们是算法工程师面试所需要具备的基础。例如今日头条算法工程师的实习生面试会问:「在圆环上随机选取 3 个点,这 3 个点组成锐角三角形的概率?」,或者其它算个积分之类的。项目作者主要为面试准备了以下几方面的知识点;
概率论
微积分本质
深度学习核心
其中深度学习核心主要包含非线性激活函数、梯度下降和反向传播。
算法题和笔试题
对于编程面试,基础算法是必不可少的,它们一般体现在笔试题上,例如数据结构、动态规划或排列组合等。很多开发者可能感觉笔试解题会很难,因为题目并不会告诉你需要用什么样的基础算法来解决,全靠我们自己一步步解析题目。这就要求我们对各种基础算法都比较熟悉,项目作者提供了以下基本算法专题:
字符串
数据结构
高级数据结构
动态规划
双指针
区间问题
排列组合
数学问题
Shuffle、采样、随机数
大数运算
海量数据处理
这些算法题会介绍具体的问题、解题思路以及对应的解题代码。例如在数据结构中,我们如何判断树 B 是不是树 A 的子树。
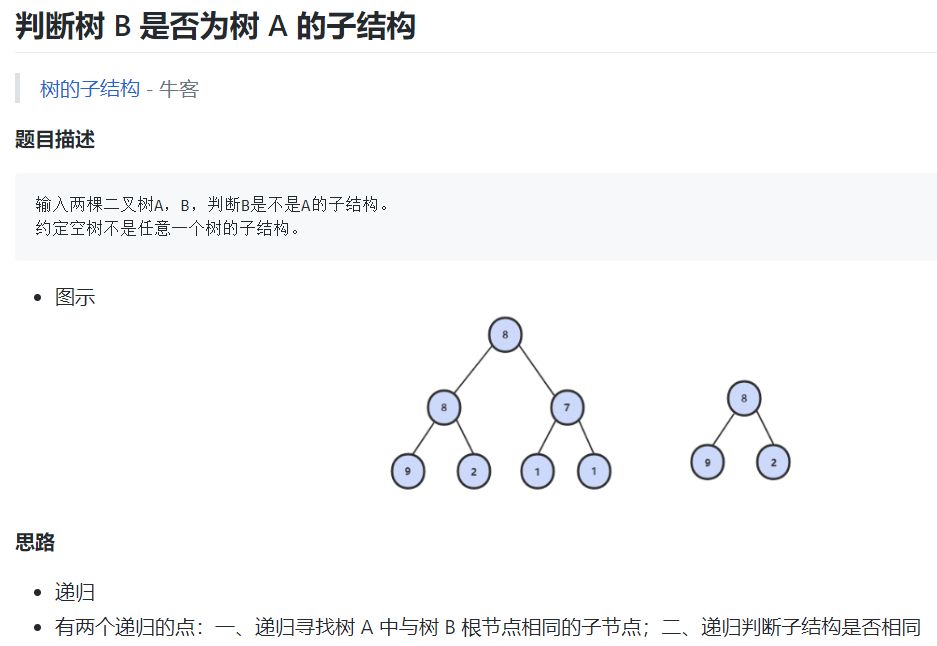
如下所示为解题代码,注意基本上各基础算法的题解都是用 C++写的,作者会引用剑指 Offer 题解和 Leetcode 题解等的解决方案。
class Solution {public: bool HasSubtree(TreeNode* p1, TreeNode* p2) { if (p1 == nullptr || p2 == nullptr) // 约定空树不是任意一个树的子结构 return false; return isSubTree(p1, p2) // 判断子结构是否相同 || HasSubtree(p1->left, p2) // 递归寻找树 A 中与树 B 根节点相同的子节点 || HasSubtree(p1->right, p2); } bool isSubTree(TreeNode* p1, TreeNode* p2) { if (p2 == nullptr) return true; // 注意这两个判断的顺序 if (p1 == nullptr) return false; if (p1->val == p2->val) return isSubTree(p1->left, p2->left) // 递归判断左右子树 && isSubTree(p1->right, p2->right); else return false; }};
此外,该项目还提供了 IO 模板和必备算法模板。作者表示不少笔试不像 LeetCode 那样可以自动完成 I/O,我们需要手动完成数据 I/O,而且如果我们没有 ACM 经验,很可能会在这上面浪费很多时间。因此这里总结的几种常见 IO 模板对于编程面试有很大的帮助,另外的算法模板同样也是。
例如如果我们输入不定数量个 Input,且以某个特殊输入为结束标志,那么用 C 语言实现的模板为:
// 示例 1int a, b;while (scanf("%d %d", &a, &b) != EOF && (a != 0 && b != 0)) { // ...}// 或者while (scanf("%d %d", &a, &b) != EOF && (a || b)) { // ...}// 示例 2int n;while (scanf("%d", &n) != EOF && n != 0) { // ...}
用 C++实现的模板为:
// 示例 1int a, b;while (cin >> a >> b) { if (a == 0 && b == 0) break; // ...}// 示例 2int n;while (cin >> n && n != 0) { // ...}
面试真题
最后,项目作者还收集了十多家科技企业面试真题,并介绍从一面到三面的内容与经验。

例如以下是头条/字节跳动-深度学习/NLP 方向的三面概览:

具体的面试题也会提供,如下所示为字节跳动 18 年 8 月的笔试题:积分卡牌游戏。

当然给了题目,对应的解决方案也会提供:
# 输入处理n = int(input())x, y = [], []for i in range(n): _x, _y = list(map(int, input().split())) x.append(_x) y.append(_y)xy = list(zip(x, y))xy = sorted(xy, key=lambda t: t[1])ret = 0if sum(x) % 2 == 0: # 如果所有 x 的和为偶数 print(sum(y)) # 直接输出所有 y 的和else: for i in range(len(xy)): if xy[i][0] % 2 == 1: # 去掉 x 中为奇数的那一项 ret = sum([xy[j][1] for j in range(len(xy)) if j != i]) print(ret) break
-
TCP协议面试常问知识点总结2023-12-15 1428
-
华为射频工程师面试经验分享2023-04-14 3591
-
C语言与C++面试知识点总结2022-05-12 1883
-
史上最全面Java面试汇总(面试题+答案)精选资料分享2021-07-21 1695
-
算法工程师面试是一门玄学吗2019-08-16 2404
-
算法工程师的面试真的是一门玄学吗2019-07-29 2559
-
深信服面算法工程师面试经历2019-03-22 4283
-
如何准备算法工程师的面试需要知道哪些知识技能2019-02-03 5994
-
面试官谈软件工程师面试技巧2018-10-25 5053
-
前端工程师面试技巧2018-10-15 4333
-
硬件工程师面试心得2014-09-14 3123
-
数字IC设计工程师笔试面试经典100题(大部分有答案)2012-08-20 73003
-
PCB布线知识面试题_PCB工程师必备2011-11-24 5706
-
FPGA工程师面试试题2011-03-02 24225
全部0条评论

快来发表一下你的评论吧 !

