

基于直方图算法的FPGA设计架构
可编程逻辑
描述
引言
直方图统计在图像增强和目标检测领域有重要应用,比如直方图均衡,梯度直方图。直方图的不同种类和统计方法请见之前的文章。本章就是用FPGA来进行直方图的计算,并且利用FPGA的特性对计算过程进行加速。安排如下:
首先基于直方图算法进行FPGA架构设计,这里主要考虑了如何加速以及FPGA资源的利用两个因素;最后基于system Verilog搭建一个验证系统。
FPGA设计架构
不论是图像灰度直方图还是梯度直方图,本质上是对数据的分布进行计数。从FPGA角度来看,只关心以下几点:
1) 根据数据大小确定其分布区间,统计分布在不同区间的数据个数,区间的大小可以调节,比如灰度直方图区间为1,梯度直方图通常大于1;
2) 如何利用FPGA对直方图统计进行加速,以及如何考虑到芯片有限资源;
首先来考虑加速方式,直方图统计过程用伪代码表示为:
For(int i=0;i Index = get_index(data[i]);
Hist[index]++;
}
Get_index函数是为了确定数据属于哪个区间,如果区间大小为1,那么index就是数据自身。如果区间是平均分布,那么就需要进行数据的大小比较。如果区间大小是2的幂次,那么index只需要数据进行移位得到。
FPGA在加速计算中最主要就是利用并行化和流水线,并行化就是将一个任务拆解成多个子任务,多个子任务并行完成。而流水线是在处理一个子任务的时候,下一个来的子任务也可以进行处理,处理模块不会等待。流水线本质上是对子任务也进行“分割”,分割的每一块可以在处理模块中同时进行。
统计N个数据,可以将N分成M份,在FPGA上同时进行M个统计,用伪代码表示为:
For(int k=0;k //并行化
For(int i=0;i Index = get_index(data[k][i]);
Hist[k][index]++;
}
}
如果区间不是2的幂次,就需要比较器,这样并行M次,就需要M个同等比较器,这对资源消耗很大。因此目前设计仅仅支持2的幂次的区间。整个设计架构如图1.2。
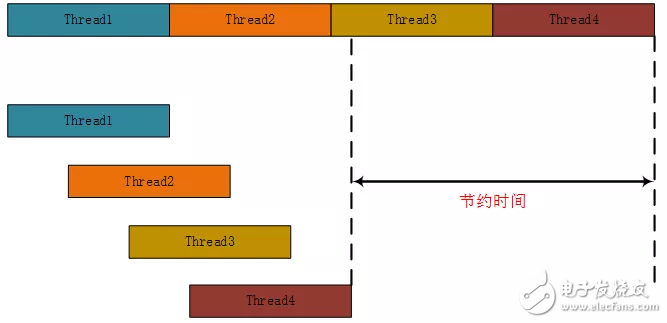
图2.1 流水线处理
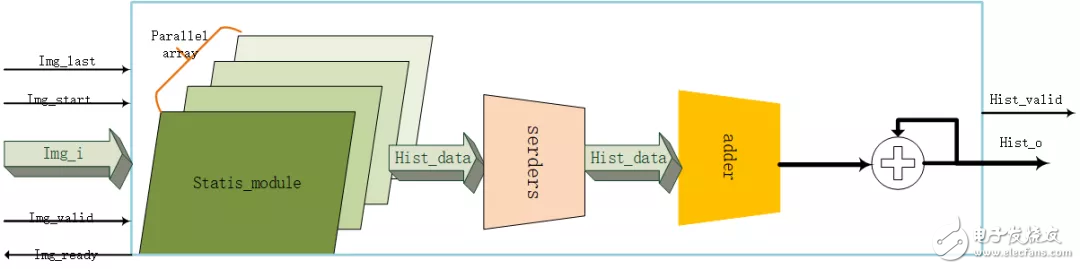
图2.2 直方图统计架构
主要分为以下几个模块:
1)statis:这个是核心计算模块,统计数据分布。ram中存放直方图统计数据,地址对应着数据分布区间。这里有一个问题需要考虑,在对ram中直方图统计数据计数时,需要读出然后计数。如果ram读端口没有寄存器,那么读出来直接加1,再写入。但是这样并不好,因为ram不经过寄存器时序不好。所以增加了一级寄存器,这样就造成了写入的延时,那么有可能下一次数据来临也会读取同样地址的数据,此时读取到的直方图数据就是还没有写入的。为了解决这个问题,判断进入的前后两个数据是否相同,如果相同就不写入而继续计数,如果不同就写入。并行多个statis模块的代码为:
genvar i;
generate
for(i=0;i
statis #(
.PIX_BW(PIX_BW),
.HIST_BW(HIST_BW),
.ADDR_BW(HIST_LEN_BW),
.BIN_W(BIN_W)
)u_statis(
.clk(clk),
.rst(rst),
.clr(clr),
.enable(1‘b1),
.pix_valid(pix_valid),
.pix(img_i[i*PIX_BW +: PIX_BW]),
.hist_rd(branch_hist_rd),
.hist_raddr(branch_hist_raddr),
.hist(branch_hist[i*HIST_BW +: HIST_BW])
);
end
endgenerate
2)serders:这个是并转串。M个statis模块会产生M组hist结果,这些结果还要进行求和,那么就要用到加法树,如果M较大,会造成加法树很大,多以这里加了serders可以调节加法树资源。
3) addTree:加法树。
module addTree #(
parameter DATA_BW = 32,//bit width of data
parameter TREE_DEPTH = 3,//depth of the add tree
parameter ADD_N = 4//add number
)
(
input clk,
input rst,
input [ADD_N*DATA_BW-1:0] adnd_x,
input [ADD_N*DATA_BW-1:0] adnd_y,
input adnd_valid,
output reg[DATA_BW-1:0] finl_sum,
output reg finl_sum_valid
);
reg [TREE_DEPTH-1:0]midl_valid;
genvar dept_i, leaf_i;
generate
for(dept_i=TREE_DEPTH-1;dept_i》=0;dept_i=dept_i-1)begin: ADD_DPET
localparam LEAF_N = 2**dept_i;
wire[DATA_BW-1:0] midl_sum[LEAF_N-1:0];
for(leaf_i=0;leaf_i
reg [DATA_BW-1:0] midl_add_x;
reg [DATA_BW-1:0] midl_add_y;
if(dept_i==TREE_DEPTH-1)begin
always @(posedge clk)begin
midl_add_x midl_add_y end
end
else begin
always @(posedge clk)begin
midl_add_x midl_add_y end
end
adder #(
.DATA_BW(DATA_BW)
)
u_adder(
.adnd_x(midl_add_x),
.adnd_y(midl_add_y),
.sum(midl_sum[leaf_i])
);
end
if(dept_i==TREE_DEPTH-1)
always @(posedge clk)begin
midl_valid[dept_i] end
else
always @(posedge clk)begin
midl_valid[dept_i] end
end
endgenerate
always @(posedge clk)begin
finl_sum end
always @(posedge clk)begin
if(rst)
finl_sum_valid else
finl_sum_valid end
endmodule
4) accum:累加器。如果加法树没有完成M个hist数据的求和,那么就需要通过累加器来完成。
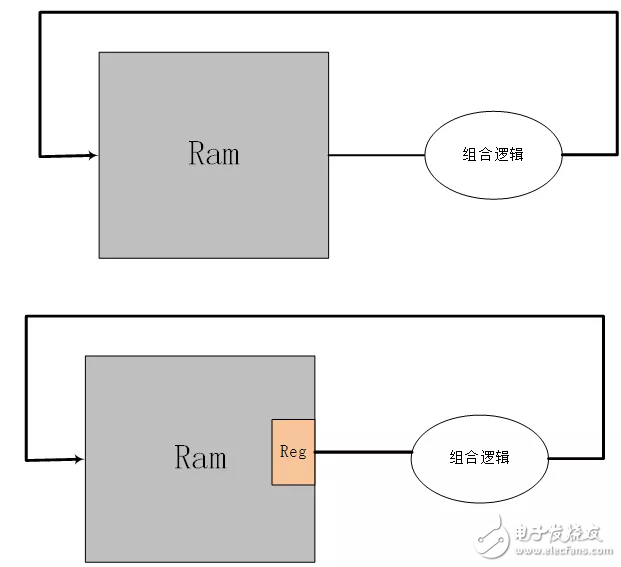
图2.3 对ram的处理
验证结构
1) img_trans:这个是随机化图像数据定义,主要通过SV中constraint来对图像大小做一些约束;
class img_trans;
rand int img_w;
rand int img_h;
rand int img_blank;
rand logic[`PIX_BW-1:0] img[`MAX_IMG_W*`MAX_IMG_H];
constraint img_cfg_cnst{
img_w img_w 》 0;
img_w % `PARALL == 0;
img_h img_h 》 0;
img_blank img_blank 》= 0;
}
extern function void write(input string f_name);
endclass
2) driver:产生image并且发送给DUT,同时通过mailbox发送给ref_model用于对比;
class img_obj;
logic [`PIX_BW-1:0] img_que[$];
endclass
class driver;
int img_w;
int img_h;
int img_blank;
logic [`PARALL*`PIX_BW-1:0] img;
logic [`PIX_BW-1:0] img_ele;
img_obj imgObj;
img_trans imgTrans;
extern task drive(mailbox img_mbx, virtual img_inf.test imgInf);
endclass
3) ref_model:自己统计直方图和DUT的结果进行比对;
class ref_modl;
logic [`PIX_BW-1:0] img;
int addr;
img_obj imgObj;
int hist[`HIST_LEN];
extern task calc(input logic clk, mailbox img_mbx);
extern task comp(virtual img_inf.test imgInf);
extern task run(input logic clk, mailbox img_mbx, virtual img_inf.test imgInf);
extern function void clear();
endclass
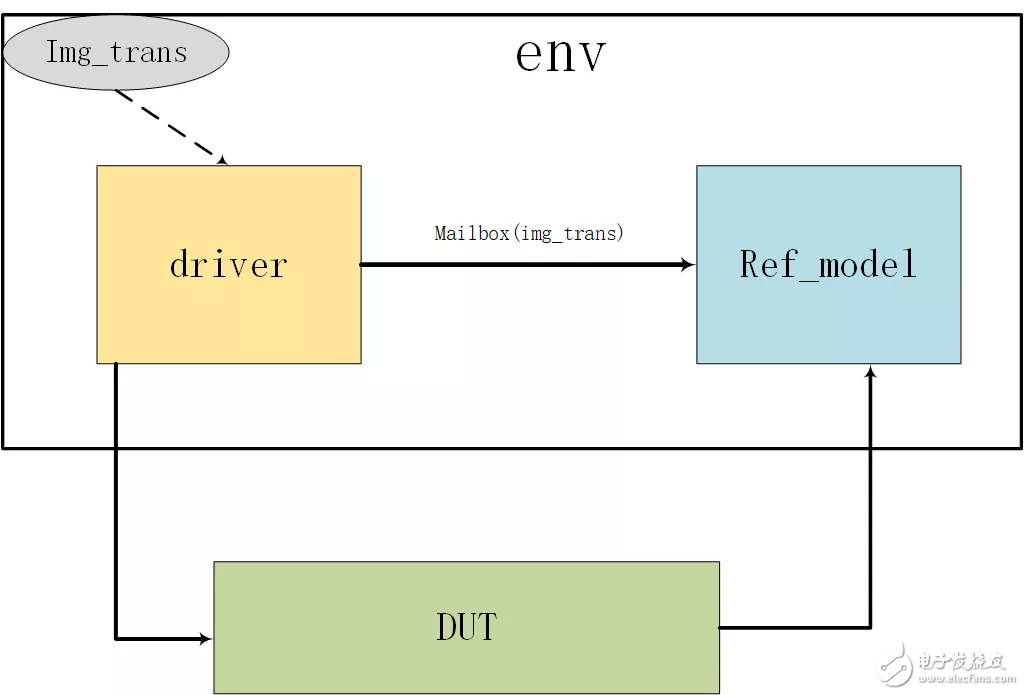
图3.1 验证架构图
最后添加一下modelsim仿真波形文件和结果,纯粹为了增加篇幅。
图3.2 modelsim仿真波形和结果
-
基于直方图算法进行FPGA架构设计2020-12-10 3549
-
一文带你了解FPGA直方图操作2024-01-10 1301
-
基于FPGA的HDTV视频图像灰度直方图统计算法设计2012-05-14 5881
-
急求直方图均衡化的Verilog代码或者是FPGA上算法处理的资料,多谢了2015-06-02 5953
-
基于FPGA的图像直方图实时显示2019-07-12 2890
-
基于FPGA的图像直方图均衡处理2019-07-14 3246
-
如何实现HDTV视频增强算法中灰度直方图统计?2021-04-30 1514
-
保持图像细节的直方图均衡算法2010-11-09 922
-
基于FPGA的视频图像灰度信号直方图均衡算法实现设计2018-07-20 3077
-
基于直方图中轴化策略的图像融合算法2017-12-06 1193
-
如何用FPGA的Block RAM性能实现HDTV视频增强算法中灰度直方图统计2019-07-10 3482
-
如何使用直方图条件熵实现水声数据分类的算法2021-01-20 820
-
基于直方图条件熵的水声数据分类算法2021-04-21 892
-
剖析FPGA灰度直方图线性拉伸2021-07-02 3864
-
基于FPGA实现图像直方图设计2024-12-24 1256
全部0条评论

快来发表一下你的评论吧 !

