斯坦福学者提出GIoU，目标检测任务的新Loss

本文是对 CVPR2019 论文《Generalized Intersection over Union: A Metric and A Loss for Bounding Box Regression》的解读，通过对 Loss 的修改提升检测任务的效果，觉得思路很棒。

该文作者来自斯坦福大学与澳大利亚阿德莱德大学。

IoU是检测任务中最常用的指标，由于IoU是比值的概念，对目标物体的scale是不敏感的。然而检测任务中的BBox的回归损失(MSE loss, l1-smooth loss等）优化和IoU优化不是完全等价的（见下图）。

而且 Ln 范数对物体的scale也比较敏感。这篇论文提出可以直接把IoU设为回归的loss。然而有个问题是IoU无法直接优化没有重叠的部分。为了解决这个问题这篇paper提出了GIoU的思想~

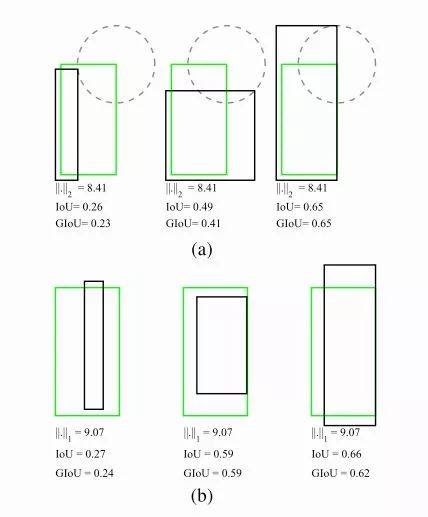
IoU与L2范数的优化不是等效的。要将IoU设计为损失，主要需要解决两个问题：

预测值和Ground truth没有重叠的话，IoU始终为0且无法优化

IoU无法辨别不同方式的对齐，比如方向不一致等。

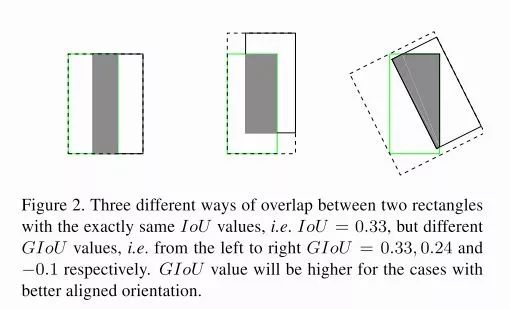
IoU 无法代表 overlap 的方式

GIoU

所以论文中提出的新 GIoU 是怎么设计的呢：

假如现在有两个任意性质 A，B，我们找到一个最小的封闭形状C，让C可以把A，B包含在内，然后我们计算C中没有覆盖A和B的面积占C总面积的比值，然后用A与B的IoU减去这个比值：

GIoU有如下性质：

与IoU类似，GIoU也可以作为一个距离，loss可以用 （下面的公式）来计算

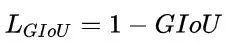
同原始 IoU 类似，GIoU 对物体的大小不敏感。GIoU 总是小于等于 IoU，对于 IoU，有

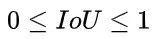
GIoU 则是

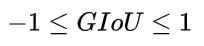
在两个形状完全重合时，有

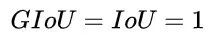
由于 GIoU 引入了包含 A，B 两个形状的 C，所以当 A，B 不重合时，依然可以进行优化。

总之就是保留了IoU的原始性质同时弱化了它的缺点。于是论文认为可以将其作为IoU的替代。

GIoU 作为 BBox 回归的损失

具体一点，如何计算损失呢？我们以 2D detecation 为例：

假设我们现在有预测的 Bbox 和 groud truth 的 Bbox 的坐标，分别记为：

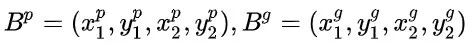
注意我们规定对于预测的 BBox 来说，有

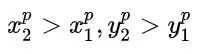
主要是为了方便之后点的对应关系。

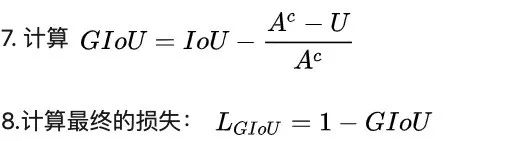
作者做了一系列的实验（针对分割任务和分类任务有一定 loss 的调整设计，不过论文中没有详细给出）结果是 IoU loss 可以轻微提升使用 MSE 作为 loss 的表现，而 GIoU 的提升幅度更大，这个结论在 YOLO 算法和 faster R-CNN 系列上都是成立的：

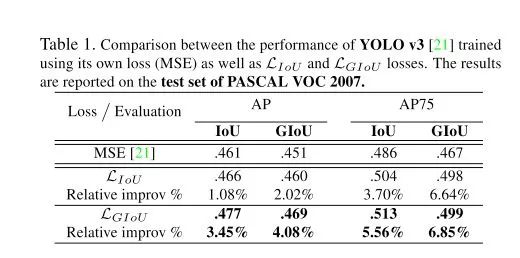
PASCAL VOC 2007上的提升with Yolo

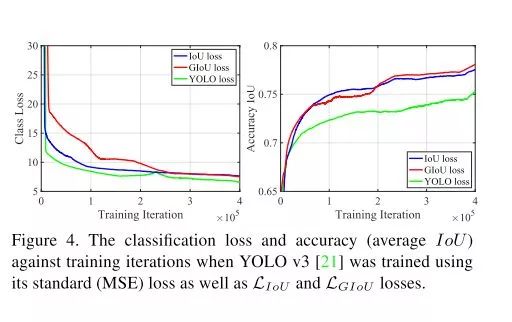
MS COCO的提升with Yolo

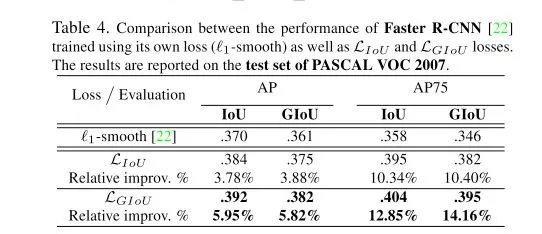
PASCAL VOC 2007 with faster-RCNN

更多内容大家可以参考项目主页：

https://giou.stanford.edu/

代码实现：

https://github.com/generalized-iou

原文链接：

https://zhuanlan.zhihu.com/p/57992040