

什么是科学假设?什么是统计假设?什么又是机器学习假设呢?
电子说
描述
什么是科学假设?什么是统计假设?什么又是机器学习假设呢?
虽然同为假说,这三个东西其实还真不太一样!
今天,就带你来区分一下“假设”三兄弟。
了解完它们的区别后,你会对假设一词在不同领域会有更深刻的认识,对于更好的使用假设会有更深入的理解。同时,对于机器学习的入门者来说,这样一篇文章对于个人今后在该领域的发展就是如虎添翼。
通常,我们所理解的监督性机器学习,是一个类似于研究从输入映射到输出的目标函数问题。
这个过程可以被分为如何选取假设空间,以及评估候选的假设空间。
作为一个机器学习领域的初学者来说,假设这个词的概念可能让他们会产生困惑,有时会产生歧义,比如在统计领域我们会有假设检验,而在科学领域我们又会有科学假说。
这些定义互有关联,却不尽相同。
所以什么是假设呢?
假设是一种对事物的解释。
它是一种凭借经验和知识所提出的猜测性想法,需要一定的评估依据。
一个好的假设是可验证的,验证结果有可能是对的,也可能是错的。
在科学界,假说一定是可以被证伪的,即通过观察检验结果,可以证实这个假说是错误的。同时,在验证结果出来之前,假说的框架结构一定要确定好。
...任何一个或一系列假说想要成为科学定理或者科学理论,一定要满足这样一个基本条件—那就是,它是可以被证伪的。
选自《What is This Thing Called Science?》1999年,第三版,第61-62页
一个好的假说既能满足现有证据,又可以用来预测新的观察或新的情况。
一个假说如果说完全满足现有证据,同时可以被验证,那么它将会成为理论或者成为理论的一部分。
小结一下,科学假说是指符合证据、同时可以被证实或者被反驳的猜测性解释。
统计学中的假设又该如何定义呢?
大多统计问题是研究观测样本之间潜在关系。
统计学上的假设检验通常是计算产生“影响”的临界值,通过计算临界值可以来判定观测样本之间是否存在某种关系。
如果似然值很小,这种影响结果就可能会是真实的,如果似然值很大,那我们可能观测到了统计波动,这种影响可能并不真实。
举例来说,通过推断两组样本之间均值所存在的关系,可以判断它们是否具有相同的统计分布,或者它们之间又有哪些差异。
举个例子,我们可以假设两组样本的均值相同。
这种假设对我们来说没什么影响,也叫作零假设。通过假设检验,我们可以得到拒绝该假设或者保留该假设。即便我们不能拒绝零假设,也不等于我们接受零假设是对的,因为结果只是一个概率。
..在社会科学研究中,我们通过建立假设、制定标准来衡量是否保留或拒绝我们的假设,通常都是零假设。
《Statistics in plain English》2010年第三版,64-65页
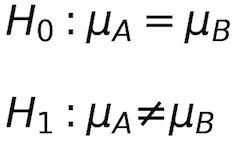
在我们的例子中,如果零假设被否定,其相对立的备择假设就认为均值之间存在差异。
零假设(H0):没有影响
备择假设(H1):存在影响
统计学中的假设检验通常不会评判影响的大小,只会近似估计被观测样本之间是否存在差异。
小结一下,统计学中的假设指的是用概率来解释样本观测值之间是否存在关系。
最后,什么是机器学习中的假设呢?
机器学习,尤其是监督性学习,是用已有数据学习得到一个最佳的函数来表示输入到输出之间的映射关系。
说的专业些,这个叫做函数逼近。就是说我们想找到一个接近于我们目标函数(我们假设它存在)的方程,可以满足在问题定义域里所有观测结果都可以从输入映射到输出结果。
在机器学习中,一个近似目标函数并且将输入映射到输出的模型被称为假设。
算法选取(比如神经网络)和算法配置(如网络拓扑和超参数)决定了模型可能表示的假设空间。
机器学习算法的学习是寻找最接近目标函数的假设,即将已选取的假设空间转化成最佳或最优的假设。
“学习”是在可能的假设空间中寻找一个表现良优的假设空间,即使在训练集之外新样本上也能适用。
选自《Artificial Intelligence: A Modern Approach》2009年第二版,第695页。
这种机器学习的框架很常见,通常可以帮助我们选取算法、理解学习和泛化问题,甚至是“偏差-方差”的权衡。举例来说,训练集通常是学习假设,而测试数据集是用来评估假设。
我们通常会用小写(h)来表示给予的特定假设,用大写(H)来表示被探索的假设空间。
假设(h):单一假设,如一个实例或特定的候选模型,可以将输入映射到输出,同时也可以对模型进行评估和预测。
假设集(H):一个包括所有可能的输入映射到输出之间关系的假设空间,通常受选取的问题框架、模型和模型调参所限制。
在选择算法和配置过程中,我们需要选取一个对目标函数来说是最好的逼近函数作为假设空间。这是非常具有挑战的,通常对于一系列不同的假设空间进行抽查会更为有效。
如果假设空间包含真函数,则学习问题是可实现的。不幸的是,我们不能总是判断一个给定的学习问题是否可以实现,因为真正的函数是未知的。
选自《Artificial Intelligence: A Modern Approach》2009年第二版,697页。
这是一个困难的问题。通常,我们通过限制假设空间的大小和评估假设的复杂性来简化搜索过程。
假设空间的表达性和假设搜索的复杂性之间存在一种权衡关系。
选自《Artificial Intelligence: A Modern Approach》2009年第二版,697页。
小结一下,机器学习中的假设是一个近似目标函数的候选模型,用于表示输入样本到输出样本之间的映射关系。
总 结
让我们重新梳理一遍对假设的三个定义:
科学假说是一种对于观察现象的猜测性解释,并且是可以被证伪的。
统计中的假设是用概率的方式来解释数据样本之间的关系。
机器学习中的假设是一个近似目标函数的候选模型,用于表示输入样本到输出样本之间的映射关系。
机器学习的假设定义要比科学中的定义更加广泛。
和科学假说一样,机器学习也是基于现有证据,可以被证伪,并对新情况进行预测。
在机器学习中的假设:
涵盖现有证据:即训练数据集
可以被证伪:有一个测试集来评估模型表现,并且与基础模型作对比,确定训练过程是否有效。
适用于新的情况:可被用来对新数据集进行预测。
-
机器学习的推荐系统运作假设2019-04-12 1316
-
思考驱动创新,创新驱动发展:如何才<敢于>大胆假设和小心求证2020-12-17 3647
-
思考驱动创新,创新驱动发展:基于假设(Assumption)的思考技术2020-12-21 2320
-
基于假设流量的Deltoid算法阈值设定2009-04-18 786
-
基于椭圆假设的电子罗盘误差补偿方法2009-06-22 759
-
基于统计假设测试的图像结构检测方法及修复2011-09-09 880
-
关于假设检验的一种合理推导2012-11-07 542
-
基于多模型势概率假设密度滤波的跟踪方法2017-12-01 665
-
PCB的物理结构和常见假设2021-03-12 2599
-
基于假设检验理论的信号统计分辨研究2021-06-18 740
-
基于渐弱假设簇的密钥属性加密方案2021-06-21 687
-
假设检验|第六章:原假设和备择假设2022-11-07 4912
-
华为周红:建设智能世界的假设与愿景-从经验、知识到智能2023-04-20 1724
-
硅片制造的光刻设置和工艺可变性假设2024-06-25 354
-
假设检验的功效和样本数量2025-01-15 845
全部0条评论

快来发表一下你的评论吧 !

